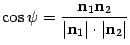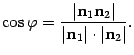Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору ⇐ ПредыдущаяСтр 7 из 7
Найдем уравнение плоскости, проходящей через точку
Общее уравнение плоскости После преобразования, уравнение
Уравнение плоскости, проходящей через три данные точки Пусть плоскость проходит через точки
Это уравнение, которому удовлетворяют координаты
Нормальное уравнение плоскости Положение плоскости Пусть
Общее уравнение плоскости
где знак берется противоположным знаку свободного члена Угол между плоскостями. Пусть плоскости
Плоскости, пересекаясь, образуют четыре двугранных угла (рис. 11.6): два тупых и два острых или четыре прямых, причем оба тупых угла равны между собой, и оба острых тоже равны между собой. Мы всегда будем искать острый угол. Для определения его величины возьмем точку
Рис.11.6.Угол между плоскостями
Если через точку
Рис.11.7.Угол между нормальными векторами острый
Рис.11.8.Угол между нормальными векторами тупой
В одном варианте (рис. 11.7) Во втором варианте (рис. 11.8)
то в обоих случаях По определению скалярного произведения
и соответственно
Так как координаты нормальных векторов известны, если заданы уравнения плоскостей, то полученная формула (11.4) позволяет найти косинус острого угла между плоскостями. Если плоскости перпендикулярны, то перпендикулярны и их нормальные векторы. Получаем условие перпендикулярности плоскостей:
Если плоскости параллельны, то коллинеарны их нормальные векторы. Получаем условие параллельности плоскостей
|
 перпендикулярно вектору
перпендикулярно вектору  , называемому нормалью к плоскости. Для любой точки плоскости
, называемому нормалью к плоскости. Для любой точки плоскости 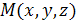 вектор
вектор  ортогонален (перпендикулярен) вектору
ортогонален (перпендикулярен) вектору 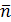 , следовательно, их скалярное произведение равно нулю:
, следовательно, их скалярное произведение равно нулю: или
или  .
.
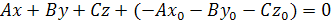 , приняв
, приняв 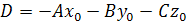 , получаем общее уравнение плоскости
, получаем общее уравнение плоскости
 .
Уравнение плоскости в отрезках
Если же общее уравнение плоскости является полным
.
Уравнение плоскости в отрезках
Если же общее уравнение плоскости является полным
 ,
,
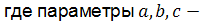 равны величинам отрезков, отсекаемых плоскостью на координатных осях.
равны величинам отрезков, отсекаемых плоскостью на координатных осях.
 и
и 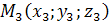 , не лежащие на одной прямой и
, не лежащие на одной прямой и  ,
, ,
, 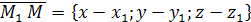 компланарны. Следовательно, их смешанное произведение равно нулю. Используя координатную запись смешанного произведения, получаем:
компланарны. Следовательно, их смешанное произведение равно нулю. Используя координатную запись смешанного произведения, получаем: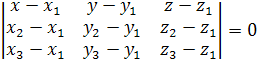 .
. любой точки, лежащей на искомой плоскости, является уравнением плоскости, проходящей через три данные точки.
любой точки, лежащей на искомой плоскости, является уравнением плоскости, проходящей через три данные точки. вполне определяется заданием единичного вектора
вполне определяется заданием единичного вектора  , имеющего направление перпендикуляра
, имеющего направление перпендикуляра  , опущенного на плоскость из начала координат, и длиной p этого перпендикуляра
, опущенного на плоскость из начала координат, и длиной p этого перпендикуляра , а
, а  – углы, образованные единичным вектором
– углы, образованные единичным вектором 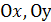 и
и 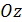 ;
;  Возьмем на плоскости произвольную точку
Возьмем на плоскости произвольную точку  и соединим ее с началом координат. Образуем вектор
и соединим ее с началом координат. Образуем вектор  . При любом положении точки Μ на плоскости
. При любом положении точки Μ на плоскости  на направление вектора
на направление вектора 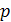 :
:  , т.е.
, т.е.  или
или 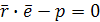 – нормальное уравнение плоскости в векторной форме. Записав его в координатах получим нормальное уравнение плоскости в координатной форме:
– нормальное уравнение плоскости в векторной форме. Записав его в координатах получим нормальное уравнение плоскости в координатной форме: .
.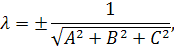
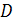 общего уравнения плоскости.
общего уравнения плоскости. и
и  заданы соответственно уравнениями
заданы соответственно уравнениями  и
и  . Требуется найти угол
. Требуется найти угол  между этими плоскостями.
между этими плоскостями.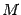 на линии пересечения плоскостей и в этой точке в каждой из плоскостей проведем перпендикуляры
на линии пересечения плоскостей и в этой точке в каждой из плоскостей проведем перпендикуляры  и
и 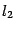 к линии пересечения. Нарисуем также нормальные векторы
к линии пересечения. Нарисуем также нормальные векторы 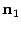 и
и 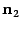 плоскостей
плоскостей 
 , перпендикулярную линии пересечения плоскостей
, перпендикулярную линии пересечения плоскостей 

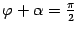 и
и  , следовательно, угол
, следовательно, угол  между нормальными векторами равен углу
между нормальными векторами равен углу  , а угол
, а угол  . Так как
. Так как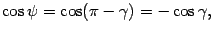
 .
. . Откуда
. Откуда