
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема Гамильтона-Кели: Каждая матрица является корнем своего характеристического многочлена
(В лекциях без док-в., если f-характ. многочлен, то f(А)=0)
№40 Опр. Собственным вектором Св-ва собств. вект 1) Каждому собств. вектору x соответствует (!) собственное значение [ctv: 2) Если x – собст. вектор оператора Т. Если (ctv) Пусть (2)-(3) = Лин. комб. содержит лишь (k-1) векторов. Действуем на (*) преобр. f, затем умножаем (*) на №41 Теорема (Критерий подобия квадратных матриц) Две квадратные матрицы подобны т.и.т.т.к., когда они являются матрицами одного и того же лин. преобр. в разных базисах Дост. Пусть A и B — квадр. порядка n над полем P, являются матрицами одного и того же лин. преобр. пр-ва V, тогда B=C -1AC (*), C-матрица перехода, С
Необ. Существ. Подобные матрицы порядка n–A,B При заданном базисе между квадратичными матрицами n мерного линейного пространства существует взаимно-однозначное соответствие (по цветочку) Пусть f линейное преобразование пр-ва V, которое в некотором базисе
№42Алгоритм нахождения собственных значений и собственных векторов линейного оператора
Пусть
ОСЛУ (**) относительно Пусть Аналогично отыскиваются собственные векторы отвечающие другим собственным значениям
Легко видеть, что множество всех собственных векторов с собственным значением №43 Опр. Пусть f лин.опер. n-мерного лин пр-ва V над полем P. Подпространство V’ называется инвариантным относительно f, если для
Теорема. В действительном n -мерном пр-ве V всякий лин.оператор f имеет по крайней мере одно одномерное или двумерное инвариантное пространство Пусть
1)
2) Отделяя вещ и мним. части перейдем к след.сист. (*) и (**) Введем в рассмотрение векторы Ясно, что x,y Действительно, пусть Размерность
Следствие: пусть f-лин.оператор вещ. лин. пр-ва Vразмерности (zn+1), где n-натур.,тогда существует хотя бы одно одномерное инвариантное подпр. f, т.к. у f хотя бы один собств.вектор, отвечающий вещ.собст.значению—корню многочлена
№44 Теперь будем считать, что V- евкл.пр-во (т.е. в Vопред. операция скалярного умножения)
Опр. Лин.операторы f и Теорема. Пусть f и Запишем (1) для пары векторов (f (
№45 Теорема. В конечномерном евклид. пр-ве V каждый лин. оператор обладает единств.[(!)] сопряженным. Возьмем в V ортонорм. базис Возьмем матрицу Покажем, что f и Из (1)=>(по теореме о матрицах сопряженных операторов) (f ( Возьмем
На основание (2) получаем, что
Что означает что соотношение Единственность доказывается (ctv), с помощью утвержд.: «Если u
№46 Опр. Лин.оператор самосопряженный(сс), если он совпадает со своим сопряжением, т.е. f=f*
|
||||||
|
Последнее изменение этой страницы: 2020-10-24; просмотров: 195; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.30.253 (0.022 с.) |
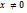 оператора
оператора  будем называть такой вектор, для которого выполняется равенство
будем называть такой вектор, для которого выполняется равенство 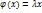 ,
,  называется собственным значением, соответ. собственному вектору x оператора
называется собственным значением, соответ. собственному вектору x оператора 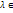 P (C).
P (C). .
.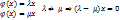 ]
] то
то  вектор
вектор  , где
, где 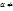 0, тоже является собст. вект. для собств. зн.
0, тоже является собст. вект. для собств. зн. 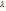 (
(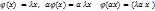 ]
]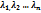 – различные собств. значения, то соответствующие им собств. вект.
– различные собств. значения, то соответствующие им собств. вект. 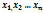 – образуют лин.независ. систему.
– образуют лин.независ. систему.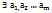 не все=0
не все=0 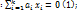 пусть для определенности
пусть для определенности 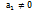 . Подействуем преобр.f на обе части(1):
. Подействуем преобр.f на обе части(1): 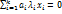 (2);
(2); 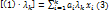 ;
; =0 (*)
=0 (*)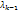 , затем из первого результата вычитаем второй => уничтожится еще один вектор, продолжая данную процедуру, придем к равенству:
, затем из первого результата вычитаем второй => уничтожится еще один вектор, продолжая данную процедуру, придем к равенству: 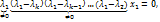 но тогда
но тогда 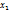 = 0, но
= 0, но 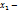 собственный вектор=>
собственный вектор=> 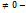 против.
против. 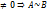
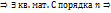 выполняется (*)\
выполняется (*)\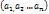 имеет матрицу A, т.к C
имеет матрицу A, т.к C 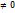 , то она служит матрицей перехода преобразования f в базисе
, то она служит матрицей перехода преобразования f в базисе 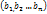
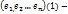 базис пр-ва V. А f лин. оператор,
базис пр-ва V. А f лин. оператор, 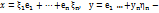 собственный вектор f=> f(x)=
собственный вектор f=> f(x)= 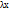 (2)
(2)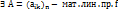 в (1)=>перепишем (2) как
в (1)=>перепишем (2) как 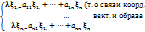 )
) 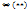
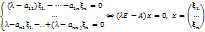
 допускает
допускает 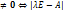 =0 (*). Т.е. нужно решить многочлен n-степени, относительно
=0 (*). Т.е. нужно решить многочлен n-степени, относительно 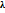 (характеристич. многочл. преобр. f) => собств. значения обязательно должны быть корнями характерист. уравнения, =>для отыскания необходимо решить(*)
(характеристич. многочл. преобр. f) => собств. значения обязательно должны быть корнями характерист. уравнения, =>для отыскания необходимо решить(*)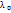 -корень этого ур. Подставим его в (**) и решим систему относительно
-корень этого ур. Подставим его в (**) и решим систему относительно  , тем самым найдем координаты собственного вектора
, тем самым найдем координаты собственного вектора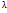 совпадает с множеством всех
совпадает с множеством всех 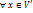 образ
образ 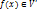 . Иначе
. Иначе 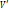 инвариантно относительно f если
инвариантно относительно f если 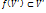 .
.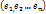 - какой-нибудь базис в пр-ве V и пусть
- какой-нибудь базис в пр-ве V и пусть 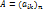 - матр. оператора f в этом базисе, тогда
- матр. оператора f в этом базисе, тогда 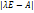 многочлен n степени с вещ. коэф. Существует 2 возможных случая: хар. многочлен имеет корень
многочлен n степени с вещ. коэф. Существует 2 возможных случая: хар. многочлен имеет корень 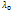
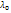 -вещественный. Тогда система для нахождения собст.вектора (*) имеет ненулевое решение, кот.опред. собстве вектор отвеч.
-вещественный. Тогда система для нахождения собст.вектора (*) имеет ненулевое решение, кот.опред. собстве вектор отвеч. 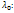
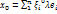 . Очевидно, одномерное подпр. L(
. Очевидно, одномерное подпр. L(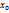 )-инварант. подпр. относительно f
)-инварант. подпр. относительно f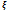 +
+ 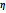 i-компл. Подставим корень в сист. (*) получим, что она имеет
i-компл. Подставим корень в сист. (*) получим, что она имеет 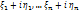 (‘) Подставляя (‘) в (*), перенесем члены с
(‘) Подставляя (‘) в (*), перенесем члены с 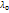 в правую часть получим
в правую часть получим 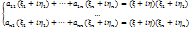
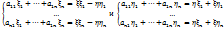
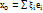 и
и 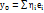
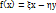 , f(y)=
, f(y)= 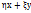 (***),=> подпространство порожденное векторами x и y (L(x,y)) инвариантное подпр. oператора f(x)
(***),=> подпространство порожденное векторами x и y (L(x,y)) инвариантное подпр. oператора f(x)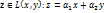 , f(z)=
, f(z)= 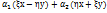 =
= 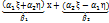 y=
y= 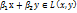
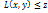 . Подпр.
. Подпр. 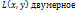 , т.к. если бы
, т.к. если бы 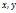 были лин.завис. y=kx, то f(x)s w:ascii="Cambria Math" w:fareast="Times New Roman" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:sz w:val="14"/><w:sz-cs w:val="12"/><w:lang w:val="EN-US"/></w:rPr><m:t>О·y</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>">
были лин.завис. y=kx, то f(x)s w:ascii="Cambria Math" w:fareast="Times New Roman" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:sz w:val="14"/><w:sz-cs w:val="12"/><w:lang w:val="EN-US"/></w:rPr><m:t>О·y</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>"> 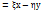 =
= 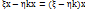 и x был бы собственным вектором преобр с вещ.собств. значением
и x был бы собственным вектором преобр с вещ.собств. значением 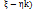 , что невозможно
, что невозможно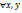 имеет место равенство
имеет место равенство 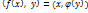 . Очевидно
. Очевидно 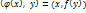 . (1)
. (1) сопряженные операторы в V,
сопряженные операторы в V, 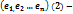 ортонорм. базис в V. А—мат. f, а В — мат
ортонорм. базис в V. А—мат. f, а В — мат 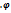 в (2). Тогда
в (2). Тогда 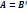
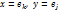 :
: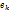 ),
), 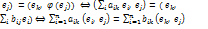
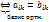 (
(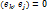 )
) 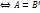
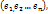 f-лин. преобр. пр-ва, матр f
f-лин. преобр. пр-ва, матр f 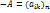 в этом базисе.
в этом базисе.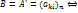
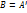 (1). Известно, что матрице
(1). Известно, что матрице  при заданном базисе отвечает (!) оператор
при заданном базисе отвечает (!) оператор 
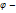 сопряженные операторы.
сопряженные операторы.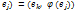 (2), т.е. для базисных векторов выполняется соотношение
(2), т.е. для базисных векторов выполняется соотношение 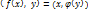 (@)
(@)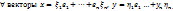 И рассмотрим скаляр. произвед.
И рассмотрим скаляр. произвед. 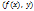 и
и 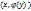
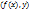 =
= 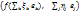 =
= 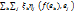
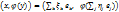 =
= 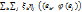
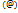 выполняется для
выполняется для 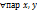 , т.е. у
, т.е. у 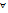 лин.оператора f
лин.оператора f 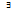 сопряженный—f*. Тогда (@) –
сопряженный—f*. Тогда (@) – 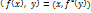
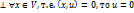 »
»


