
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
ЛЕММА 2.2. (откладывание вектора от точки)
Для любого вектора Доказательство. Сначала докажем конструктивно, что такая точка существует. Пусть Определение 2.2. Говорят, что вектор Определение 2.3. Векторы Очевидно, что если Определение 2.4. Пусть
и обозначается Очевидно, что
Сложение векторов Определение 3.1. Суммой двух векторов
Покажем, что сумма векторов не зависит от выбора точки Действительно, пусть Так как Замечание 3.1. Для нахождения суммы неколлинеарных векторов приходится строить треугольник
Свойства сложения векторов. ТЕОРЕМА 3.1. Для произвольных векторов 1. 2. 3. 4. Доказательство. 1. Пусть
По правилу треугольника 2. Пусть 3. Применим правило Значит, 4. Применим правило Замечание 3.2. 1. Суммой векторов
2. Аналогично можно определить сумму 3. Для неколлинеарных векторов при их сложении можно пользоваться правилом параллелограмма: Разность векторов. Определение 4.1. Разностью векторов Докажем существование и единственность разности. Таким образом, доказано существование и единственность разности любых двух векторов, при этом эта разность обозначается
Разностью двух данных векторов, отложенных из одной точки является вектор, идущий из конца второго в конец первого.
Отметим еще равенство Умножение вектора на число. Определение 5.1. Произведением вектора 1. 2. Из условия 1. следует, что В дальнейшем вместо записи Напомним определение гомотетии, известное из школьного курса геометрии. 1. точки 2. 3. Предварительно докажем одну лемму. ЛЕММА 5.1. Если при гомотетии с центром в точке Доказательство. По определению гомотетии имеем
|
||||||
|
Последнее изменение этой страницы: 2020-10-24; просмотров: 348; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.196.182 (0.022 с.) |
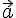 и любой точки
и любой точки 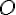 существует единственная точка
существует единственная точка 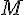 такая, что
такая, что  .
.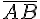 — представитель вектора
— представитель вектора 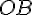 точку
точку 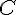 . Далее строим точку
. Далее строим точку 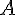 относительно точки
относительно точки  совпадают, то по лемме 1.1.
совпадают, то по лемме 1.1. 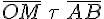 , значит,
, значит, 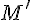 такая, что
такая, что  . Тогда получаем
. Тогда получаем 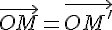 , следовательно, по лемме 2.1.
, следовательно, по лемме 2.1.  . Поэтому точки
. Поэтому точки 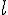 , если любой его представитель либо параллелен этой прямой, либо лежит на ней.
, если любой его представитель либо параллелен этой прямой, либо лежит на ней.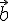 называются коллинеарными, если они параллельны одной и той же прямой (мы пишем
называются коллинеарными, если они параллельны одной и той же прямой (мы пишем 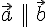 ).
).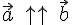 (если сонаправлены любые их представители), либо противоположно направлены
(если сонаправлены любые их представители), либо противоположно направлены 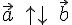 (если противонаправлены любые их представители). Снова условимся считать, что нулевой вектор сонаправлен любому вектору
(если противонаправлены любые их представители). Снова условимся считать, что нулевой вектор сонаправлен любому вектору 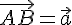 . Вектор
. Вектор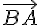 называется противоположным к вектору
называется противоположным к вектору 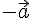 .
.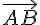 противоположен вектору
противоположен вектору 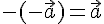 .
.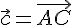 , где
, где 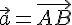 ,
, 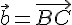 ,
, 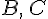 — точки, полученные после откладывания векторов
— точки, полученные после откладывания векторов 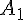 --- любая точка, отличная от точки
--- любая точка, отличная от точки 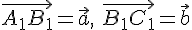 . Докажем, что
. Докажем, что 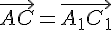 .
.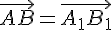 и
и 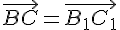 , то по лемме2.1.
, то по лемме2.1. 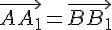 и
и  , то есть
, то есть 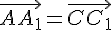 . Следовательно, по той же лемме
. Следовательно, по той же лемме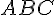 . Поэтому правило сложения векторов называется правилом треугольника. Из этого правила следует, что для любых трех точек
. Поэтому правило сложения векторов называется правилом треугольника. Из этого правила следует, что для любых трех точек 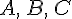 справедливо равенство
справедливо равенство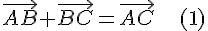
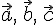 справедливы следующие равенства:
справедливы следующие равенства: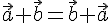 --- коммутативность сложения векторов.
--- коммутативность сложения векторов.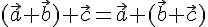 --- ассоциативность сложения векторов.
--- ассоциативность сложения векторов.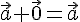 .
.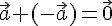 .
.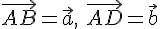 , а затем от точки
, а затем от точки 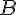 отложим вектор
отложим вектор 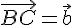 . Согласно построению
. Согласно построению 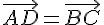 , поэтому по лемме 2.1. получаем
, поэтому по лемме 2.1. получаем 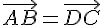 , т.е.
, т.е. 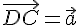 .
.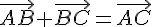 и
и 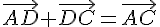 , следовательно,
, следовательно, 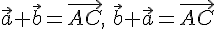 . Отсюда получаем, что
. Отсюда получаем, что 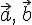 и
и  --- произвольные векторы. Возьмем какую-нибудь точку
--- произвольные векторы. Возьмем какую-нибудь точку 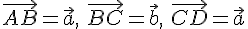 .
. 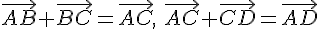 , поэтому
, поэтому 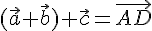 . С другой стороны
. С другой стороны  , поэтому
, поэтому 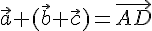 . Отсюда получаем требуемое.
. Отсюда получаем требуемое.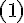 к точкам
к точкам 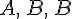 получим
получим .
.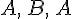 получим
получим 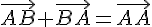 .
.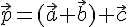 . На основании доказанной теоремы
. На основании доказанной теоремы 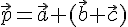 , поэтому при записи суммы трех векторов можно опустить скобки и писать просто
, поэтому при записи суммы трех векторов можно опустить скобки и писать просто  . Более того, можно доказать, что сумма трех векторов не зависит от порядка слагаемых. В самом деле, докажем, например, что
. Более того, можно доказать, что сумма трех векторов не зависит от порядка слагаемых. В самом деле, докажем, например, что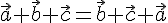 :
: .
.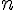 векторов, где
векторов, где 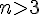 . Пусть
. Пусть 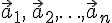 --- произвольные векторы. Их суммой называется вектор
--- произвольные векторы. Их суммой называется вектор 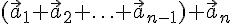 , и обозначается так:
, и обозначается так: 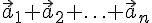 .
. 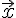 , который в сумме со вторым вектором дает первый вектор.
, который в сумме со вторым вектором дает первый вектор.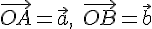
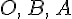 получаем
получаем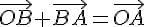
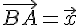 , будем иметь
, будем иметь 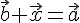 . Этим доказано существование разности.
. Этим доказано существование разности. такой, что
такой, что 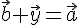 . Тогда
. Тогда 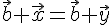 . Прибавим к обеим частям этого равенства вектор
. Прибавим к обеим частям этого равенства вектор 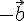 . Получим
. Получим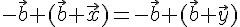
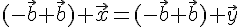
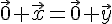
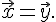
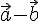 .
.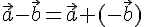

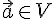 на действительное число
на действительное число 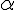 называется вектор
называется вектор 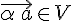 , который удовлетворяет двум условиям:
, который удовлетворяет двум условиям: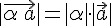 ;
;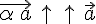 , если
, если 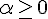 и
и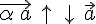 , если
, если  .
.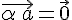 тогда и только тогда, когда
тогда и только тогда, когда 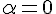 или
или  .
.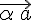 будем употреблять запись
будем употреблять запись 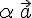
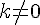 называется такое преобразование плоскости, при котором каждой точке
называется такое преобразование плоскости, при котором каждой точке  лежат на одной прямой;
лежат на одной прямой;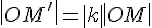 ;
;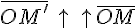 , если
, если 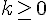 и
и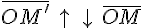 , если
, если 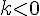 .
.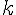 треугольник
треугольник 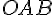 переходит
переходит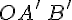 , то
, то  .
.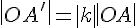 и
и 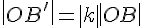 , поэтому
, поэтому 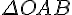 подобен
подобен 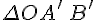 с коэффициентом
с коэффициентом 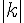 . Отсюда следует, что
. Отсюда следует, что 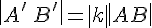 и
и 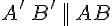 . Если
. Если 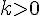 , то точки
, то точки 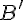 лежат по одну сторону от прямой
лежат по одну сторону от прямой 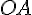 , поэтому
, поэтому 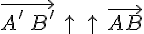 , следовательно,
, следовательно, 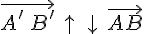 , т.е. и в этом случае
, т.е. и в этом случае 


