
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Пункт В - сравнение с учетом приоритетов локальных критериев
Способы задания и учета приоритета локальных критериев Обычно используются три способа; с помощью ряда приоритета, вектора приоритета и весового вектора. Ряд приоритетов, в данной задаче он следующий Это чисто качественный способ задания приоритетов. При таком способе обычно используется принцип «жесткого приоритета», т.е. не допускается ни малейшего снижения критерия, стоящего левее в ряду приоритета. Вектор приоритета Вектор приоритета
У нас вектор приоритета имеет вид: Задание приоритета с помощью весового вектора. Весовой вектор
Компонента
(3)
переходят к вектору. И тогда выбор наилучшего варианта производится с помощью всего вышеописанного во второй части аппарата, только вместо компонент вектора Для случая 5-ти локальных критериев соотношение (3) переписывается в виде:
где Преобразуем нашу таблицу, учитывая весовые коэффициенты. Умножаем первый и второй столбцы на 0,28, третий - на 0,24, четвертый - на 0,12, а пятый - на 0,08. Получаем:
Таблица 4
Рассмотрим все те принципы, которые мы рассматривали во второй части (пункт А). Теперь будем использовать минимум теории, в основном только расчеты.
Принцип равномерности Он провозглашает целесообразный выбор такого варианта решения, принадлежащего области компромиссов, при котором достигалась бы некоторая равномерность показателей по всем локальным критериям. Используя следующие реализации принципа равномерности: А) Принцип равенства. Б) Принцип квазиравенства. В) Принцип максимина. Принцип равенства
Он провозглашает целесообразность выбора такого варианта, при котором все значения локальных критериев равны между собой. В данном случае принцип равенства не работает. Принцип квазиравенства
Практически достичь равенства локальных критериев не удаётся, тогда лучшим признаётся вариант, в котором локальные критерии более близки к этому равенству. В нашем случае принцип квазиравенства не работает. Принцип максимина
Для каждого варианта выбирается минимальное значение локального критерия, и окончательный выбор останавливается на варианте, в котором этот минимум достигает своего максимума. В этом случае равномерность обеспечивается за счёт подтягивания локального критерия с наименьшим значением показателя. Max (0,102; 0,102; 0,08; 0,116; 0,082) = 0,116 => оптимальным признаётся вариант №4 Вывод После рассмотрения принципа равномерности мы получили: ) принцип равенства не работает; ) принцип квазиравентсва не работает; ) принцип максимина признаёт оптимальными вариант №4.
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-03-27; просмотров: 336; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.134.90.44 (0.011 с.) |
||||||||||||||||||||||||||||||||||||||||||||||||
 =((1,2),3,4,5), указывает на то, что локальные критерии, записанные в скобках левее, более важны, чем локальные критерии, записанные правее, а критерии, расположенные в скобках, обладают одинаковой важностью, т.е. самыми важными являются критерии
=((1,2),3,4,5), указывает на то, что локальные критерии, записанные в скобках левее, более важны, чем локальные критерии, записанные правее, а критерии, расположенные в скобках, обладают одинаковой важностью, т.е. самыми важными являются критерии  и
и  , вторым по важности являются критерии
, вторым по важности являются критерии  , затем
, затем 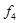 и, наконец,
и, наконец,  .
. - это способ количественного задания приоритетов. Компоненты этого вектора
- это способ количественного задания приоритетов. Компоненты этого вектора  определяют степень относительного превосходства двух соседних критериев ряда приоритета, т.е.
определяют степень относительного превосходства двух соседних критериев ряда приоритета, т.е.  важнее критерия
важнее критерия 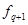 , в том случае, если
, в том случае, если  и
и  . Для удобства
. Для удобства  , всегда равно единице (
, всегда равно единице ( =1).
=1). определяется в результате попарного сравнения локальных критериев, предварительно упорядоченных в соответствии с рядом приоритета
определяется в результате попарного сравнения локальных критериев, предварительно упорядоченных в соответствии с рядом приоритета  . Очевидно, что любой компонент вектора приоритета
. Очевидно, что любой компонент вектора приоритета  удовлетворяет соотношению:
удовлетворяет соотношению: ,
, 
 представляет собой k-мерный вектор, компоненты которого связаны соотношениями:
представляет собой k-мерный вектор, компоненты которого связаны соотношениями: ,
,  ,
, 
 показывает степень относительного превосходства критерия
показывает степень относительного превосходства критерия 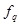 над всеми оставшимися критериями. Обычно, если необходимо количественно задавать приоритет критериев, то его задают в виде вектора приоритета, поскольку там сравнение идет только между двумя соседними критериями; затем с помощью соотношения:
над всеми оставшимися критериями. Обычно, если необходимо количественно задавать приоритет критериев, то его задают в виде вектора приоритета, поскольку там сравнение идет только между двумя соседними критериями; затем с помощью соотношения: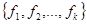 используются компоненты
используются компоненты  Такой подход называют принципом гибкого приоритета.
Такой подход называют принципом гибкого приоритета. ,
, ,
, ,
, ,
,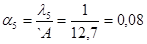 ,
, +
+  +
+  +
+  +
+  = 3,6+3,6+3+1,5+1=12,7
= 3,6+3,6+3+1,5+1=12,7







