
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Способы реализации случайного механизма выбора стратегий
Для реализации применения игроком его активных стратегий с оптимальными вероятностями (относительными частотами), необходимо иметь случайный механизм выбора стратегий. Например, если оптимальная смешанная стратегия Игральную кость можно использовать при относительных частотах 1:5; 2:4; 1:1; 4:2; и так далее до 5:1. Секундная стрелка часов может служить для выбора случайных чисел от 0 до 59, если только игрок не смотрел на часы недавно и не знает наперед, даже приблизительно, ответ. Но на практике могут потребоваться любые сочетания чисел в качестве относительных частот. Механизмом, удовлетворяющим вышеуказанному требованию, является датчик случайных чисел R от 0 до 1 с равномерной плотностью вероятности. Так как стратегии А1, А2,..., Аm несовместны (в каждый момент, применяется лишь одна из этих стратегий) и образуют полную группу событий
Рис. 2.12
Возникает вопрос: а как же реализуется сам датчик случайных чисел R? Самый простой из датчиков случайных чисел (ДСЧ) - это вращающийся барабан, в котором перемешивается перенумерованные шары. Пусть, например, нам надо разыграть случайное число R от 0 до 1 с точностью 0.001. Заложим в барабан 1000 перенумерованных шаров и после, случайным образом выбранного одного из шаров, разделим его номер на 1000. Можно поступить и иначе: вместо1000 шаров заложить только 10, с цифрами 0, 1, 2,...., 9. Вынув случайным образом первый шар, получаем первый десятичный знак дроби. Вернув шар в барабан и прокрутив его, выберем случайным образом второй шар - его номер даст второй десятичный знак и т.д. Можно доказать, что получаемые таким образом десятичные дроби будет иметь равномерное распределение от 0 до 1. Достоинством этого способа в том, что он может обеспечить любую точность задания числа R. На практике широко применяются таблицы случайных чисел. Ниже приведен пример такой таблицы (рис.2.13). Числа сгруппированы лишь для удобства пользования таблицей. Можно начинать с любой точки таблицы, отсчитывать числа вверх или вниз, группировать числа.
Как использовать таблицу случайных чисел, чтобы получить желаемые относительные частоты? Возьмем в качестве примера оптимальную стратегию
Рис.2.13 Часто желательно модифицировать этот способ. Например, в случае относительных частот 8:3 сумма чисел равна 8+3=11. Приходится применять двухзначные числа от 00 до 99. Но чтобы не отбрасывать числа от 11 до 99, разделим 99 на 11, получаем 9 (в общем случае это будет смешанная дробь). Далее умножаем 8×9=72 и 3×9=27. Теперь, если выбранное двухзначное число лежит в пределах от 00 до 71, используем первую стратегию, а если от 72 до 99, - то вторую. Число 99 будем отбрасывать.
Для получения R на ЭВМ применяются специальные датчики случайных чисел. Это могут быть как “физические датчики”, принцип действия которых основан на преобразовании случайных шумов, так и вычислительные алгоритмы, по которым сама машина вычисляет так называемые “псевдослучайные” числа. Один из самых простых алгоритмов вычисления псевдослучайных чисел состоит в следующем. Берут два произвольных n-значных числа a1 и a2 и перемножают их, и в полученном результате берут n средних знаков. Так получают число а3. Затем перемножают а2 и а3 и в полученном результате берут n средних чисел, получая число а4,и т.д. Полученные таким образом числа рассматриваются как последовательность двоичных дробей с n знаками после запятой. Такая последовательность дробей практически ведет себя как ряд случайных чисел R от 0 до 1. В заключение изложения матричных игр отметим, что хотя само понятие смешанной стратегии требует многократного повторения партий игры, полученные результаты справедливы и к играм, которые играются только один раз, поскольку все изложения теории были выведены применительно к одной партии игры. Качественно аргументировать этот тезис можно следующим образом: очевидно, что если противник узнает, какую мы выбрали стратегию, то предпримет ход, который будет иметь для нас наихудшие последствия. Поэтому единственным выходом является использование для выбора стратегии случайного механизма (жребия), результат которого противник не может предвидеть (хотя, конечно, ему может и повезти). Теория игр указывает характеристики (частоты применения стратегий), которыми должен обладать используемый случайный механизм.
ТЕСТЫ (В – Верно, Н – Неверно) 1. Каждая матричная игра может быть представлена парой прямой и двойственной задач линейного программирования. 2. Преимуществом приближенного метода Брауна-Робинсона является то, что объем вычислений с увеличением размерности игры m*n растет существенно медленнее, чем в методах линейного программирования. 3. Теория игр не может дать результатов в тех случаях, когда элементы платежной матрицы заданы неточно (например, когда они только упорядочены). 4. Случайные числа выдаваемые датчиком случайных чисел, используемые для реализации оптимальных стратегий, должны быть распределены по равномерному закону. 5. Теория игр применима и для игр, которые играются только один раз. Ответы: (1 - В; 2 - В; 3 - Н; 4 – В, 5- В). ЗАДАЧИ Решить матричные игры, имеющие платежные матрицы вида:
ПОЗИЦИОННЫЕ ИГРЫ Общие сведения В общих играх число игроков может быть больше двух, некоторые ходы возможно являются случайными, игроки могут иметь по несколько ходов, причем информация о прошедшем может меняться от хода к ходу. Такие игры называются позиционными или играми в развернутой форме. Пример. Выборы с правом вето. Пусть три игрока (N=3) выбирают одного из четырех (G=4) кандидатов в президенты. Правило выбора таково: начиная с первого игрока, каждый игрок налагает вето на выбор одного из неотведенных кандидатов. Единственный оставшийся кандидат считается избранным. Функции выигрышей Ui для каждого из игроков в зависимости от выбранного в президенты кандидата имеют вид:
В развернутой форме данная игра может быть представлена в виде следующего дерева игры (рис. 3.1.), где около ветвей поставлены номера отводимых кандидатов, а у конечных вершин – номера победивших кандидатов. Если победил, например, кандидат под номером 4, то выигрыш первого игрока будет равен 7, а для второго и третьего игроков – 4.
Позиционные игры должны включать следующие элементы описания: * последовательность личных и случайных ходов игроков; * выборы, которые могут делать игроки при каждом личном ходе;
Рис.3.1
* исходы случайных ходов и распределение вероятностей этих исходов; * информацию, доступную игрокам при выполнении личного или случайного хода; * правила окончания игры и подсчеты выигрыша игроков. Число ходов в данной игре не фиксируется. В общем случае, оно зависит от последовательности выборов, исходов. Однако, правила должны гарантировать, что игра в конце концов закончится. Относительно ходов правила игры имеют следующую структуру. Для первого хода правила указывают его вид. Если это личный ход, то правила перечисляют возможные варианты и указывают игрока, который делает выбор. Если это случайный ход, то перечисляются возможные варианты и обуславливаются вероятности их выбора. Для последующих ходов Задание позиционной игры в виде дерева Позиционные игры удобно задавать графически в виде дерева игры (рис.3.2.). Дерево состоит из вершин, соединенных между собой ветвями. Вершины дерева называют еще позициями игры, а его ветви - ходами игрока.
Рис.3.2
Основными свойствами дерева игры являются: * дерево содержит одну единственную начальную вершину (“корень” дерева), в которую не входит ни одна ветвь; * дерево имеет не менее одной вершины, из которой не выходит ни одна ветвь. Эти вершины называются конечными вершинами; * из корня дерева имеется единственный путь к каждой из остальных вершин дерева. Вершина соответствует определенному состоянию игры перед очередным ходом. Каждую вершину занимает только один игрок, и ей присваивается номер, равный номеру игрока, который делает выбор. Вершины, соответствующие случайным ходам, обозначают номером 0. Ветви, выходящие из вершины, изображают выборы, которые могут быть сделаны игроком при данном ходе. Вероятности выполнения случайного хода записывают у соответствующих ветвей. Возле конечных вершин дерева указываются исходы игры - значения выигрыша игроков (а в антагонистических играх – выигрыш первого игрока). Партия начинается с корня (нижней вершины). Каждый ход есть изменение позиции, соответствующее перемещению из одной вершины на какую-нибудь из примыкающих верхних вершин. Число ветвей у вершины равно числу вариантов хода. Партия заканчивается при достижении одной из конечных вершин. Величина
В зависимости от выбора игроков возможно столько различных партий игры, сколько конечных вершин у дерева. Очевидно, если в игре нет случайных ходов, и каждый из игроков выбрал свою стратегию, то исход игры однозначно определен. Для игры со случайными ходами, результат партии становится случайной величиной, поэтому необходимо случайные выигрыши заменить их математическими ожиданиями. Как совокупность всех решений, которые должен принять игрок, можно описать как одно решение - выбор стратегии, так и совокупность случайных ходов, может быть заменена одним случайным испытанием Н. В рассматриваемом примере (рис.3.2) случайное испытание Н может иметь следующие исходы: Н=|(Г,3),(Г,2),(Р,3),(Р,2)|, с вероятностями Игра, полученная путем усреднения случайных исходов, не полностью эквивалентна исходной игре, так как она характеризует не частный результат отдельной партии, а средние исходы большого числа партий. Информация, доступная игрокам задается информационным разбиением вершин на множества V i, называемые классами информации или информационными множествами. Если достигнута вершина v Î V i, то игроку, который должен ходить, указывается только класс информации, а не точное положение вершины v. Таким образом, в классы информации могут входить несколько вершин, неразличимых игроком, делающим выбор на данном ходе, т.е. игрок не в состоянии различить, какой из нескольких вершин соответствует состояние игры в данный момент времени. В рассматриваемом примере класс информации V 1 состоит из двух вершин. В том случае, когда всякий класс информации содержит только одну вершину, имеем игру с полной информацией (например, игра в шахматы). В играх с неполной информацией содержится хотя бы один класс информации с числом вершин не менее двух. При вычерчивании дерева игры классы информации обводят замкнутой линией. Игрок всегда знает, какому классу информации соответствует состояние игры в данный момент, но не знает конкретной вершины этого класса. Классы информации (информационные множества) должны удовлетворять следующим условиям: 1. содержать вершины только одного игрока; 2. каждая вершина может принадлежать только одному классу информации; 3. вершины класса информации соответствуют только одному временному ходу; 4. из всех вершин, составляющих класс информации, может выходить только одинаковое количество ветвей. Дерево, изображенное на рис.3.2., соответствует следующей игре: Первый игрок выбирает одно из двух направлений (“налево” или “направо”). Ход “налево” оценивается тремя баллами, а “направо” - четырьмя. Затем бросается жребий (монета) и, если выпадает герб, второму игроку сообщается предыдущий выбор первого игрока. Если выпадает решка, то второй игрок знает лишь, что он находится в классе информации V 1, но не знает, в какой из двух вершин этого класса он находится. Второй игрок выбирает одно из двух направлений (“налево” или “направо”). Ход “налево” оценивается пятью баллами, а “направо” - двумя. Четвертый ход является опять случайным и состоит в выборе с равными вероятностями одного из направлений: “налево”, “направо”, которые оцениваются тремя и двумя баллами соответственно. Поскольку вероятности выбора направления при случайном ходе одинаковы (равны Числа, выбранные в первом, третьем и четвертом ходах, складываются, и полученная сумма уплачивается вторым игроком первому, если она четная, в противном случае первый игрок платит второму. Пространства Ф1 и Ф2 всех возможных стратегий игроков 1 и 2 в рассматриваемом примере следующие: Ф1=|(3), (4)|; Ф2=|(3,Г,5),(3,Г,2),(3,Р,5),(3,Р,2),(4,Г,5),(4,Г,2),(4,Р,5),(4,Р,2)|, где первое число каждой стратегии в пространстве Ф2 соответствует выбору первого игрока, второе число - выпаданию герба или решки (“Г” - выпал “герб”; “Р” - выпала “решка”). Третья - выбору второго игрока пятерки или двойки. Очевидно, что если в игре нет случайных ходов и каждый из игроков выбрал свою стратегию, то исход игры однозначно определен. Описание позиционной игры в виде дерева позволяет глубже проанализировать ход игры. Вместе с тем, оптимальное поведение игроков легче определить для игры, заданной в нормальной форме (для двух игроков - в матричной форме), особенно в том случае, если игра содержит информационные множества и случайные ходы.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-03-26; просмотров: 219; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.33.107 (0.15 с.) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 (относительные частоты 1:1), то для ее реализации можно использовать подбрасывание монеты: если выдает “герб”, то применяется первая стратегия, а если “решка”, - то вторая.
(относительные частоты 1:1), то для ее реализации можно использовать подбрасывание монеты: если выдает “герб”, то применяется первая стратегия, а если “решка”, - то вторая. , то для реализации случайного механизма выбора стратегий поступают следующим образом. Делят интервал (0, 1) на m участков длиной p1, p2,..., pm (рис. 2.12). На какой из участков попало число R - ту стратегию и следует в данной партии использовать.
, то для реализации случайного механизма выбора стратегий поступают следующим образом. Делят интервал (0, 1) на m участков длиной p1, p2,..., pm (рис. 2.12). На какой из участков попало число R - ту стратегию и следует в данной партии использовать.
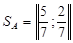 . Далее выбираем из таблицы любое однозначное случайное число. Если это число равно 0, 1, 2, 3 или 4, то используем в данной партии первую стратегию. Если число равно 5 и 6, то применяем вторую стратегию. Если это число равно 7, 8 и 9, то отбрасываем его и берем число под ним. Для следующей партии используется число ниже предыдущего.
. Далее выбираем из таблицы любое однозначное случайное число. Если это число равно 0, 1, 2, 3 или 4, то используем в данной партии первую стратегию. Если число равно 5 и 6, то применяем вторую стратегию. Если это число равно 7, 8 и 9, то отбрасываем его и берем число под ним. Для следующей партии используется число ниже предыдущего.


 правила определяют в зависимости от выбора и исходов предыдущих (
правила определяют в зависимости от выбора и исходов предыдущих ( -1) ходов, будет ли
-1) ходов, будет ли 
 называется длиной дерева.
называется длиной дерева. , где Г - означает выпадение “герба”, Р - “решки”, а цифры 2, 3 соответствуют случайному выбору на четвертом ходу.
, где Г - означает выпадение “герба”, Р - “решки”, а цифры 2, 3 соответствуют случайному выбору на четвертом ходу.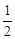 ), то их можно на графическом изображении дерева игры и не указывать.
), то их можно на графическом изображении дерева игры и не указывать.


