
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Решение матричной игры (2х2)
Пусть матричная игра G (2x2) имеет платежную матрицу
Предположим, что игра не имеет седловой точки, т.е. a¹b. При наличии седловой точки решение очевидно. В соответствии с основной теоремой игра имеет оптимальное решение в смешанных стратегиях: SA=||p1, p2|| и SB=||q1, q2||, где вероятности применения (относительные частоты применения) чистых стратегий удовлетворяют соотношениям
В соответствии с теоремой об активных стратегиях, оптимальная смешанная стратегия обладает тем свойством, что обеспечивает игроку максимальный средний выигрыш, равный цене игры n, независимо от того, какие действия предпринимает другой игрок, если тот не выходит за пределы своих активных стратегий. В частности, если игрок А использует свою оптимальную смешанную стратегию, а игрок В - свою чистую активную стратегию В1, то цена игры n равна
а при использовании игроком В чистой активной стратегии В 2, выигрыш будет равен
Уравнения (2.11), (2.13) и (2.14) образуют систему трех линейных алгебраических уравнений с тремя неизвестным: р1, р2 и n. Решая ее, легко находим, что
Если игрок В использует свою оптимальную смешанную стартегию, а игрок А - свою чистую активную стратегию А1, то цена игры n равна
а при использовании игроком А чистой активной стратегии А2, выигрыш будет равен
Уравнения (2.12), (2.18) и (2.19) образует систему трех линейных алгебраических уравнений с тремя неизвестными: q1; q2 и n. Решая ее, легко находим, что
Естественно, что в обоих случаях цена игры (выражения (2.17) и (2.22)) получилась одна и та же. Чтобы соотношения (2.15), (2.16), (2.17), (2.20), (2.21), (2.22) имели смысл, необходимо потребовать, чтобы
или
Тогда 0<p1<1; 0<p2<1; 0<q1<1; 0<q2<1. Нетрудно заметить, что в этих неравенствах отражено предположение об отсутствии в рассматриваемой игре седловой точки. Действительно, ни один из четырех выигрышей а11, а12, а21, а22 не может удовлетворить этим неравенствам, будучи минимальным в своей строке и максимальным в своем столбце.
Решения системы уравнений (2.15), (2.16), (2.17) и (2.20), (2.21), (2.22), полученные алгебраическим методом, удобно получать и графическим методом (рис. 2.4). Для нахождения вероятностей р 1, р 2 и цены игры v в прямоугольной системе координат по оси абсцисс откладывается вероятность р 1Î[0,1], а по оси ординат - соответствующие этой вероятности - выигрыши игрока А. При р1=0, игрок А применяет чистую стратегию А 2. Если при этом игрок В применяет чистую стратегию В 1, то выигрыш игрока А равен а21 (уравнение (2.13)), а если игрок В применяет чистую стратегию В 2, то выигрыш игрока А равен а22 (уравнение (2.14)). При р1=1, игрок А применяет чистую стратегию А 1.
Рис. 2.4 Если при этом игрок В применяет чистую стратегию В 1, то выигрыш игрока А равен а11, а при применении чистой стратегии В2 - а12. Так как значения р1 лежат в пределах [0,1], то соединяя крайние точки для стратегий В1 и В2 (строя графики функций vА =(a11-a21)p1+a22 и vА =(a12-a22)p1+a22), получаем значения выигрышей игрока А для всех промежуточных значений р 1. В соответствии с принципом максимина, игрок А должен выбрать такую смешанную стратегию, при которой его минимальный выигрыш максимален. Точка N пересечения отрезков прямых (рис. 2.4) и определяет как оптимальную цену игры v opt, так и оптимальные вероятности p 1opt и p 2opt=1- p 1opt, соответствующие оптимальной смешанной стратегии игрока А, т.е. дает решения системы уравнений (2.11), (2.13), (2.14). Для графического решения системы уравнений (2.12), (2.18), (2.19) отложим по оси абсцисс вероятность q1Î[0,1], а по оси ординат соответствующие этой вероятности выигрыши игрока В: vВ =(a11-a12)q1+a12; (2.23) vВ =(a21-a22)q1+a22. (2.24)
Рис. 2.5 Решением являются координат точки М пересечения прямых, описываемых уравнений (2.23) и (2.24): q1opt;q2opt=1-q1opt и v opt. Это же следует и из принципа максимина, в соответствии с которым игрок В должен выбрать такую смешанную стратегию, при которой его максимальный проигрыш будет минимальным. Для игры G(2х2) с седловой точкой геометрическая интерпретация решения быть представлена, например, следующим образом (рис.2.6).
Рис. 2.6 Стратегия В 2 игрока В является для него явно невыгодной, так как, применяя ее, он в любой случае проигрывает больше, чем при применении стратегии В 1. В данной игре р 1opt =1;р 2opt = 0; v opt =а11, т.е. игра имеет седловую точку N и решается в чистых стратегиях. Игрок А должен применять стратегию А 1, а игрок В - стратегию В1. На рис. 2.7 показан случай, в котором решением игры для игрока А является чистая стратегия А 2, а для игрока В - стратегия В 1. Игра имеет седловую точку N. Пример: Найти алгебраическим и геометрическим методами решение игры, платежная матрица которой имеет вид
Рис. 2.7 В данной игре нижняя цена игры a=1 не равна верхней цены игры b=3, поэтому игра не имеет седловой точки и, в соответствии с основной теоремой матричных игр, имеет оптимальное решение в смешанных стратегиях. Для игрока А, в соответствии с формулами (2.15) и (2.16), оптимальные вероятности применения стратегий А1 и А2 равны:
Для игрока В, в соответствии с формулами (2.20) и (2.21), оптимальные вероятности применения стратегий В1 и В2 равны:
Таким образом, оптимальные смешанные стратегии игроков
Так как n >0, то игра выгодна для игрока А. Графическое изображение игры для игрока А показана на рис. 2.8.
Рис. 2.8 Нижняя граница выигрыша игрока А определяется ломаной CND. Оптимальное решение, определяется точкой N, естественно, дает тоже решение, что и алгебраический метод: Геометрическое изображение игры для игрока В показано на рис.2.9.
Рис. 2.9 Оптимальное решение, определяемое точкой М, дает решение
ЗАДАЧИ
Определите алгебраическим и геометрическим методами оптимальные решения следующих игр 2х2:
Упрощение матричных игр Решение матричных игр тем сложнее, чем больше размерность платежной матрицы. Поэтому для игр с платежными матрицами большой размерности отыскание оптимального решения можно упростить, если уменьшить их размерность путем исключения дублирующих и заведомо невыгодных (доминируемых) стратегий. Определение 1. Если в платежной матрице игры все элементы строки (столбца) равны соответствующим элементам другой строки (столбца), то соответствующее этим строкам (столбцам) стратегии называются дублирующими. Определение 2. Если в платежной матрице игры все элементы некоторой строки, определяющей стратегию А i игрока А, не больше (меньше или некоторые равны) соответствующих элементов другой строки, то стратегия А i называется доминируемой (заведомо невыгодной). Определение 3. Если в платежной матрице игры все элементы некоторого столбца, определяющего стратегию В i игрока В не меньше (больше или некоторые равны) соответствующих элементов другого столбца, то стратегия В i называется доминируемой (заведомо невыгодной). Правило. Решение матричной игры не изменится, если из платежной матрицы исключить строки и столбцы, соответствующие дублирующим и доминируемым стратегиям. Пример. Упростить матричную игру, платежная матрица которой имеет вид:
Из платежной матрицы видно, что стратегия А2 дублирует стратегию А5, потому любую из них можно отбросить (отбросим стратегию А5). Сравнивая почленно стратегии А1 и А4, видим, что каждый элемент строки А4 не больше соответствующего элемента строки А1. Поэтому применение игроком А доминирующей над А4 стратегии А1 всегда обеспечивает выигрыш, не меньший того, который был бы получен при применении стратегии А4. Следовательно, стратегию А4 можно отбросить. Таким образом, имеем упрощенную матричную игру с платежной матрицей вида:
Из этой матрицы видно, что в ней некоторые стратегии игрока В доминируют над другими: В3 над В2, В4 и В5. Отбрасывая доминируемые стратегии В2, В4 и В5, получаем игру 3x2, имеющей платежную матрицу вида:
В этой матрице стратегия А3 доминируется как стратегией А1, так и стратегией А2. Отбрасывая стратегию А3, окончательно получаем игру 2x2 с платежной матрицей
Эту игру уже упростить нельзя, ее надо решать рассмотренным выше алгебраическим или геометрическим методом. Необходимо отметить, что отбрасывая дублируемые и доминируемые стратегии в игре с седловой точкой, мы все равно придем к игре с седловой точкой, т.е. к решению в чистых стратегиях. Но лучше сразу проверить, не обладает ли игра седловой точкой - это проще, чем сравнивать почленно все строки и все столбцы платежной матрицы. Алгебраические методы решения матричных игр иногда производить проще, если использовать также следующие свойства матричных игр. Свойство 1. Если ко всем элементам платежной матрицы прибавить (вычесть) одно и тоже число С, то оптимальные смешанные стратегии игроков не изменятся, а только цена игры увеличится (уменьшится) на это число С. Свойство 2. Если каждый элемент платежной матрицы умножить на положительное число k, то оптимальные смешанные стратегии игроков не изменятся, а цена игры умножится на k. Отметим, что эти свойства верны и для игр, имеющих седловую точку. Эти два свойства матричных игр применяются в следующих случаях: 1) если матрица игры наряду с положительными имеет и отрицательные элементы, то ко всем ее элементам прибавляют такое число, чтобы исключить отрицательные числа в матрице; 2) если матрица игры имеет дробные числа, то для удобства вычислений элементы этой матрицы следует умножить на такое число, чтобы все выигрыши были целыми числами. Пример. Решить матричную игру 2х2 с платежной матрицей вида:
Умножая все элементы платежной матрицы на 10, а затем прибавляя к ним число 2, получаем игру с платежной матрицей
Решая эту игру алгебраическим методом, получаем
В соответствии со свойствами 1 и 2, исходная матричная игра имеет те же оптимальные смешанные стратегии: Решение игр 2xn и mx2 Как уже отмечалось в теореме об активных стратегиях, любая конечная игра mxn имеет решение, в котором число активных стратегий каждого игрока не превосходит
Практически решение игры 2xn осуществляется следующим образом: 1) строится графическое изображение игры для игрока А; 2) выделяется нижняя граница выигрыша и находится наибольшая ордината нижней границы (максимин), которая равна цене игры v; 3) определяется пара стратегий игрока В, пересекающихся в точке оптимума. Эти стратегии и являются активными стратегиями игрока В. Таким образом, игра 2xn сведена к игре 2x2, которую более точно можно решить алгебраическим методом. Если в точке оптимума пересекается более двух стратегий, то в качестве активных стратегий может быть выбрана любая пара из них. Решение игры mx2 осуществляется аналогично. Но в этом случае строится графическое изображение игры для игрока В и выделяется не нижняя, а верхняя граница выигрыша (так как находится оптимальная смешанная стратегия игрока В), и на ней находится точка оптимума с наименьшей ординатой (минимакс). Пример. Найти решение игры, платежная матрица которой имеет вид:
Платежная матрица не имеет седловой точки, поэтому оптимальное решение должно быть в смешанных стратегиях. Строим графическое изображение игры для игрока А (рис.2.10)
Рис. 2.10 Точка N (максимин) является точкой оптимума. В этой точке пересекаются линии, соответствующие активным стратегиям В1 и В2 игрока В. Таким образом, исключая стратегию В3, получаем матричную игру 2x2 с платежной матрицей вида
Используя алгебраический метод решения этой игры, получаем точное решение
Ответ:
Пример. Найти решение игры, платежная матрица которой имеет вид
Платежная матрица не имеет седловой точки. Для сведения данной игры к игре 2x2 строим ее графическое изображение для игрока В (рис. 2.11). Точка М (минимакс) является точкой оптимума. В этой точке пересекаются отрезки, соответствующие активным стратегиям А2, А6 и А3 игрока А. Таким образом, исключая стратегии А1, А4 и А5 и выбирая из трех активных стратегий две (например, А2 и А3 или А2 и А6), приходим к матричной игре 2x2. Выбор стратегий А3 и А6 исключен, так как в этом случае точка М перестанет быть точкой минимакса.
Рис.2.11 Пусть выбираются стратегии А2 и А3. Тогда игра 2x2 приобретает вид
Оптимальные смешанные стратегии данной игры, а, следовательно, и исходной игры определяются следующими вероятностями:
Ответ: Другой вариант игры 2x2 получается, если использовать стратегии А2 и А6. В этом случае платежная матрица имеет вид
Тогда
Ответ: Естественно, что цена игры для обоих вариантов одинакова. В заключение наметим общую схему решения матричных игр 2xn и mx2: 1. Определяется наличие седловой точки, т.е. возможность решения игры в чистых стратегиях. Если нижняя цена игры a не равна верхней цене игры b, то осуществляется поиск решения в смешанных стратегиях. 2. Производится упрощение матричной игры путем исключения дублирующих и доминируемых стратегий. Если упрощенная игра имеет размерность не 2x2, то переходим к этапу 3. 3. Строится графическое изображение игры и определяется две активные стратегии игрока, имевшего в исходной задаче число стратегий больше двух. 4. Решается матричная игра 2x2.
ТЕСТЫ (В – Верно, Н – Неверно) 1. Если в игре 2xn нет оптимального решения в чистых стратегиях, то оптимальное решение в смешанных стратегиях содержит две активные стратегии у каждого из игроков. 2. В игре mx2 число активных стратегий в оптимальной стратегии каждого из игроков может быть равно или единице, или двум. 3. Оптимальное решение в игре двух лиц с нулевой суммой всегда является устойчивым независимо от того, смешанные или чистые стратегии используют игроки. 4. Если оптимальная цена матричной игры отрицательна, то конечный результат игры будет убыточным для игрока А. 5. Прибавление одного и того же числа ко всем элементам платежной матрицы не влияет на цену игры. 6. Умножение всех элементов платежной матрицы на одно и тоже положительное число не изменяет оптимальных стратегий игроков. 7. Цена матричной игры изменится, если из платежной матрицы исключить строки и столбцы, соответствующие дублирующим и доминируемым стратегиям. 8. Любая матричная игра 2xn или mx2 может быть сведена к игре 2х2.
Ответы: (1 - В; 2 - В; 3 - В; 4 - В; 5 - Н; 6 - В; 7 - Н; 8 - В).
ЗАДАЧИ Решить следующие матричные игры:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-03-26; просмотров: 510; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.224.197 (0.135 с.) |
 Bj
Ai
Bj
Ai
 ; (2.11)
; (2.11) . (2.12)
. (2.12)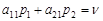 , (2.13)
, (2.13) . (2.14)
. (2.14) . (2.15)
. (2.15) . (2.16)
. (2.16) . (2.17)
. (2.17) , (2.18)
, (2.18)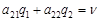 . (2.19)
. (2.19) . (2.20)
. (2.20)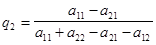 . (2.21)
. (2.21)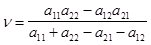 . (2.22)
. (2.22)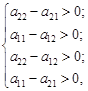




 Bj
Ai
Bj
Ai

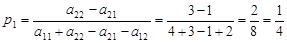 ;
; .
. ;
; .
.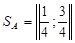 ;
;  , а цена игры в соответствии с формулой (2.22) равна:
, а цена игры в соответствии с формулой (2.22) равна: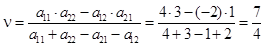 .
.
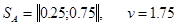 .
.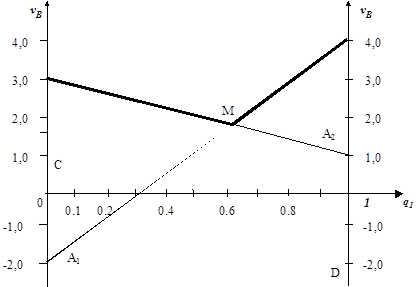
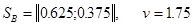 .
. Bj
Ai
Bj
Ai
 A4
A4
 A5
A5



 Bj
Ai
Bj
Ai
 Bj
Ai
Bj
Ai
 Bj
Ai
Bj
Ai
 Bj
Ai
Bj
Ai
 Bj
Ai
Bj
Ai
 ;
;  ;
; ;
;  ;
; .
. и
и  . А для получения исходной цены игры необходимо из полученной цены игры вычесть 2, а затем разделить на 10. Таким образом, получаем цену исходной игры:
. А для получения исходной цены игры необходимо из полученной цены игры вычесть 2, а затем разделить на 10. Таким образом, получаем цену исходной игры:  .
. , где
, где  . Следовательно, у игры 2xn или mx2 всегда имеется решение содержащее не более двух активных стратегий у каждого из игроков
. Следовательно, у игры 2xn или mx2 всегда имеется решение содержащее не более двух активных стратегий у каждого из игроков 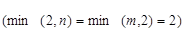 . Если эти активные стратегии игроков будут найдены, то игры 2xn и mx2 превращаются в игры 2x2, методы решения которых рассмотрены выше.
. Если эти активные стратегии игроков будут найдены, то игры 2xn и mx2 превращаются в игры 2x2, методы решения которых рассмотрены выше.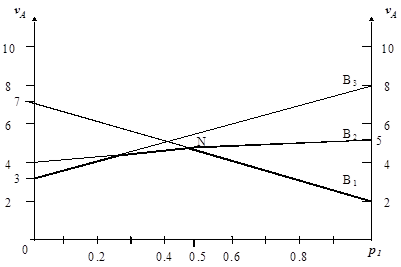
 Bj
Ai
Bj
Ai
 ;
;  ;
; ;
; 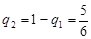 ;
; .
. ;
; 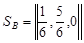 ;
;  .
. Bj
Ai
Bj
Ai

 Bj
Ai
Bj
Ai
 ;
;  ;
;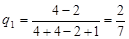 ;
;  ;
; .
. ;
;  ;
;  .
. Bj
Ai
Bj
Ai
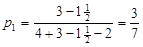 ;
;  ;
; ;
;  ;
; .
. ;
; 


