
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Решение выпуклых игр на единичном квадрате
Определение 3. Класс антагонистических игр, в которых х,у Î [0,1] называются играми на единичном квадрате. В играх на единичном квадрате любая ситуация (х,у) понимается как точка единичного квадрата. Определение 4. Бесконечная антагонистическая игра на единичном квадрате называется строго выпуклой, если ее функция выигрыша Н (х,у) строго выпукла по у при любом х. Решение выпуклых игр на единичном квадрате базируется на следующих основных теоремах [2]. Теорема 2. В строго выпуклой игре игрок 2 имеет единственную оптимальную стратегию у*, которая является чистой и является решением уравнения
Теорема 3. Пусть в выпуклой бесконечной антагонистической игре на единичном квадрате с функцией Н (х,у) дифференцируемой по у при любом х, у* - оптимальная чистая стратегия игрока 2, а 1) если у* = 1, то среди оптимальных стратегий игрока 1 имеется чистая стратегия 2) если у* = 0, то среди оптимальных стратегий игрока 1 имеется чистая стратегия 3) если 0< у*< 1, то среди оптимальных стратегий игрока 1 найдется такая, которая является смесью стратегий При этом стратегии р
Примеры решения бесконечных антагонистических игр Игра «Борьба за рынки» Пусть одна из фирм (игрок 1) пытается вытеснить другую фирму (игрок 2), имеющую два рынка сбыта, с одного из этих рынков. Общая сумма средств, выделяемых игроком 1 на эту цель, равна единице (Х Î [ 0, 1 ]). Стратегии игрока 1 состоят в распределении этих средств между двумя рынками. Если на первый рынок направляется сумма х, то на второй - (1-х). Пусть игрок 2 для удержания рынков также располагает единичной суммой средств, и его стратегия будет состоять в выделении суммы у на первый рынок и (1-у) - на второй. Считается, что игрок 1, добившись превосходства средств на одном из рынков, вытесняет своего противника с этого рынка и получает выигрыш, равный избытку своих средств, который берется с коэффициентом, характеризующим важность рынка (пусть этот коэффициент равен k1 для первого рынка и k2 для второго). Рассматриваемая игра является игрой на единичном квадрате. В этой игре пара чисел (х, у), где х,у Î [ 0,1 ] являются точками единичного квадрата.
Функция выигрыша в рассматриваемом примере
где h1>0; h2>0.
Решение. График зависимости H (х 0, y) от у для некоторого х = х 0 представлен на рис.4.1.
Рис.4.1
Очевидно, что при любых х0 функция Н (х0, у) является выпуклой функцией от у. Имеем
Поэтому цена игры
График функции
Рис.4.2
Первый член под знаком максимума с ростом у убывает, а второй - возрастает. Поэтому при малых значениях у максимум достигается на отрезке k1(1-у), а при больших - на отрезке прямой k2у. Следовательно, минимальное значение этот максимум принимает при таком у*, для которого
Таким образом, найденное у* является единственной оптимальной чистой стратегией игрока 2. Она состоит в распределении имеющихся средств между рынками пропорционально важности рынков. Значение цены игры
Далее надо найти оптимальную стратегию игрока 1. Случаи х ³ у* и х £ у* будем рассматривать порознь. Теорема 3 утверждает, что если Н(х,у) - выпукла и 0 £ у* £ 1, то среди оптимальных стратегий игрока 1 найдется такая, которая является смесью двух активных стратегий
При этом стратегии
Для случая х ³ у* уравнение (4.2) принимает вид
откуда Для случая х £ у* уравнение (4.2) имеет уже другой вид:
откуда Таким образом, активными стратегиями игрока 1 оказываются: Частные производные
Тогда уравнение (4.4) для данной игры приобретает вид
Таким образом оптимальная стратегия игрока 1 состоит в концентрации всех его средств на одном из рынков, причем вероятность выбора рынка обратно пропорциональна его важности. Этот результат объясняется просто: чем важнее рынок, тем больше средств вложит противник в его сохранение и тем меньше свободных средств останется на нем после вытеснения противника, и тем менее значимой будет победа над ним.
Игра с выбором момента времени (игра типа дуэли) Формулировка. Пусть каждый из двух игроков намерен выполнить некоторое действие (выбросить на рынок партию товара, внести на совещание предложение, произвести выстрел и т.д.). При этом обстоятельства часто складываются так, что, во-первых, целесообразно выполнить это действие как можно позже, а во-вторых, желательно своим действием упредить сходное действие противника. Такой конфликт в условиях противоположных интересов его участников естественно моделировать бесконечной антагонистической игрой на единичном квадрате, в которой функция выигрыша Н в общем случае имеет вид
где каждая из функций y и j а) непрерывна по обеим переменным; б) монотонно возрастает по х при любых значениях y; в) монотонно убывает по y при любом значении х; г) удовлетворяет условию
Игра с функцией выигрыша Н(х,у), удовлетворяющая перечисленным условиям называется игрой с выбором момента времени, или игрой типа дуэли. Мы ограничимся рассмотрением одного примера данной игры, теория которой, хотя и разработана, но достаточно сложна [2]. Пусть игроки 1 и 2 выбирают соответственно числа х и у из интервала [0,1]. Эти числа будем понимать как моменты времени выполнения ими требуемых действий. Пусть t - время появления некоторого объекта, который достается игроку, который первый после t совершил требуемое действие. Игрок, обладающий объектом, получает выигрыш, равный 1, а его противник эту единицу теряет. Если ни один из игроков не получит объект, то выигрыш каждого из игроков принимается равным нулю. Предполагается, что время появления объекта является случайной величиной, распределенной на интервале [0,1] по равномерному закону. Эту игру называют также борьбой за встречу случайно появляющегося объекта. Запишем математическое выражение функции выигрыша. Рассмотрим ситуацию (х,у), в которой х<у. В этом случае игрок 1 выигрывает единицу, если t£х; (4.7) проигрывает единицу, если х<t£y; (4.8) и не получает ничего, если y£t. (4.9) Вероятность событий (4.7), (4.8) и (4.9) равны соответственно х, (у-х) и (1-у). Таким образом, при х < у имеем
Аналогичным способом находим, что при х>у
Естественно, что при х=у, Н(х,у)=0. Схематическое описание Н(х,у) приведено на рис.4.3. Решение. Заметим, что игра является симметричной. Действительно, при х<у
Аналогично, при х > у
Наконец, при х=у
Рис.4.3
Для антагонистических симметричных игр существует теорема, утверждающая для этих игр цена игры Поэтому для решения данной задачи достаточно найти оптимальную стратегию игрока 1. Пусть оптимальная стратегия игроков имеет плотность распределения f:
Если игрок 2 применяет эту стратегию, то
С учетом формул (4.10) и (4.11.). перепишем последний интеграл
Так как
Дифференцируя тождество (4.12) по х, имеем
Вторая частная производная имеет вид
Интегрируя это дифференциальное уравнение, получаем
откуда
Полученная плотность распределения f(x) положительна и дифференцируема. Однако интеграл Можно доказать, что плотность распределения может обращаться в нуль лишь между нулем и некоторым a>0. Таким образом, имеем:
Для определения неизвестных параметров a и с воспользуемся следующими соображениями. Во-первых, f(x) должна удовлетворять условию нормировки:
Во-вторых, Из уравнений (4.15) и (4.16) можно определить значения a и с. С этой целью перепишем эти уравнения в явном виде.
Далее на основании симметричности игры
Поскольку с¹0, это нам дает
Откуда получаем Таким образом, искомая оптимальная стратегия игрока 1 определяется плотностью распределения
График f(x) изображен на рис.4.4.
Рис.4.4. Остается проверить, что найденные стратегии игроков действительно являются оптимальными. Для этого достаточно убедиться в том, что для любого х При поскольку в рассматриваемом случае
Тем самым оптимальность стратегии с плотностью f установлена.
ТЕСТЫ (В – Верно, Н – Неверно) 1. Игры называются бесконечными, если у всех игроков множество чистых стратегий бесконечно. 2. Бесконечные антагонистические игры решать труднее, чем конечные. 3. В бесконечной антагонистической игре принципом оптимальности является принцип максимина. 4. Бесконечные антагонистические игры решаются только в чистых стратегиях. 5. Играми на единичном квадрате называются такие бесконечные антагонистические игры, для которых возможные стратегии двух игроков Х и У Î [0,1]. 6. Для антагонистических симметричных игр оптимальные стратегии игроков 1 и 2 совпадают. 7. Для антагонистических симметричных игр цена игры v> 0. 8. В строго выпуклой игре игрок 2 имеет единственно оптимальную стратегию, которая является чистой.
(Ответы: 1-Н; 2-В; 3-В; 4-Н; 5-В; 6-В; 7-Н; 8-В).
ЗАДАЧИ Найти хотя бы одно решение бесконечной антагонистической игры на единичном квадрате со следующей функцией выигрыша: 1. 2. 3. 4. 5. 6.
БЕСКОАЛИЦИОННЫЕ ИГРЫ Общие сведения Антагонистические игры, которые рассматривались в предыдущих главах книги, описывают конфликты частного вида, которые не всегда адекватны разным ситуациям или вообще не могут считаться приемлемыми. В частности, антагонистические игры не затрагивают конфликты с числом игроков больше двух. Более того, даже в конфликтах с двумя игроками интересы сторон не всегда противоположны. Во многих конфликтах одна из ситуаций может оказаться предпочтительнее другой для обоих игроков. Бескоалиционные игры являются играми более общей природы. Бескоалиционность понимается в том смысле, что группам игроков (“коалициям”) не приписывается ни каких-либо интересов, за исключением тех, которые вытекают из интересов отдельных игроков. Целью каждого игрока в такой игре является только получение по возможности наибольшего индивидуального выигрыша. Определение 1. Бескоалиционной игрой называется игра N игроков (N³2), каждый из которых имеет множество стратегий Определение 2. Бескоалиционная игра называется игрой с постоянной суммой, если существует такое постоянное С, что Класс антагонистических игр является классом игр двух лиц с нулевой суммой. Определение 3. Конечная бескоалиционная игра двух игроков с ненулевой суммой называется биматричной игрой. Как и в случае антагонистических игр необходимо выработать принципы оптимального поведения игроков в бескоалиционных играх и найти решения (оптимальные стратегии каждого из игроков). Для класса антагонистических игр принципом оптимальности является принцип максимина. В общих бескоалиционных играх возможны ситуации одновременного увеличения выигрышей всех игроков или хотя бы их одновременного выигрыша, поэтому в этих играх необходимо ввести формализованное описание таких понятий, как выгодность, устойчивость и справедливость того или иного решения игры. Определение 4. Ситуация х в игре называется приемлемой для игрока і, если для любой его стратегии
т.е. при применении і-м игроком в данной ситуации всех других стратегий, его выигрыш не может увеличиться. Определение 5. Ситуация в игре, приемлемая для всех игроков, называется ситуацией равновесия по Нэшу (равновесной ситуацией). Иными словами, ситуация х называется равновесной, если для любого игрока іÎN выполняется условие (5.1). Из определения видно, что ни один из игроков не заинтересован в отклонении от своей стратегии, образующих в совокупности ситуацию равновесия. В случае антагонистической игры приемлемые стратегии игроков совпадают с их оптимальными стратегиями. Для неантагонистических игр понятие оптимальной стратегии может вообще не иметь смысла: в таких играх оптимальными оказываются не стратегии отдельных игроков, а их сочетания для всех игроков сразу. В бескоалиционных играх как оптимальные следует квалифицировать не действия того или иного игрока, а совокупность действий всех игроков.
Поэтому в бескоалиционной игре решение игры – это чаще, нахождение ситуаций равновесия. Пример 1. Игра “Семейный спор” Одна из наиболее распространенных интерпретаций игры следующая. Муж (первый игрок) и жена (второй игрок) могут выбрать одно из двух вечерних развлечений: футбольный матч или балет. Естественно предположить, что муж предпочтет футбол, а жена – балет. Однако для обоих гораздо важнее идти вместе, чем смотреть предпочитаемое зрелище в одиночестве. В данной 2х2 биматричной игре функции выигрышей Н1 и Н2 соответственного первого и второго игроков можно представить в виде
где стратегии игрока 1: А1 – выбираю футбол; А2 – иду на балет; игрока 2: В1 – иду на футбол, В2 – на балет. Очевидно, что для первого игрока предпочтительнее ситуация (А1, В1), а для второго (А2, В2), и эти ситуации являются равновесными. Однако в данном примере как будет показано ниже, есть еще и третья ситуация равновесия, состоящая в выборе игроками смешанных стратегий: Однако выигрыши каждого из игроков в этой ситуации равновесия меньше, чем в двух первых ситуациях равновесия, где они равны 2 или 1, в зависимости от ситуации и игрока. Хотя стратегии (А1,В1) и (А2,В2) являются оптимальными, поскольку дают максимальные выигрыши, однако приносят игрокам не одинаковые выигрыши, поэтому не являются справедливыми. Отметим также, что если в матричной игре ни одному из игроков не выгодно информировать противника о своей стратегии, то в данной биматричной игре это свойство не выполняется. Действительно, если игроки не общаются до игры и оба обладают твердыми характерами, т.е. первый игрок выбирает стратегию А1, а второй – В2, то в результате они оба проигрывают. Аналогичная ситуация получиться и в том случае, когда каждый из игроков имеет мягкий характер и решает уступить.Так сочетание устойчивости со справедливостью вступает в противоречие с сочетанием устойчивости и выгодности. Лучшим для игроков в рассматриваемой игре является договорный вариант (А1,В1) или (А2,В2), причем справедливым решением будет их выбор одного из этих вариантов путем бросания монеты. Выпадение герба будет означать, например, что семейство идет на матч по футболу, а решки – на балет. Заметим, что в антагонистической игре в отличие от биматричной нет смысла вести переговоры до игры и уславливаться о совместном плане действий. В рассматриваемой игре, ясно, что если игроки договорились бы играть оба, скажем первую чистую стратегию, причем игрок 1 за получение большего выигрыша, чем игрок 2, заплатил бы ему 1/2, то решение было бы выгодным и справедливым для обоих игроков. Однако в рамках бескоалиционных игр такого рода дележи не предусматриваются.
|
|||||||||
|
Последнее изменение этой страницы: 2020-03-26; просмотров: 347; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.55.14 (0.101 с.) |
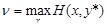 , где
, где  - цена игры.
- цена игры.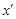 , для которой
, для которой 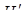 y(
y(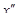 , для которой
, для которой 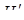 y(
y(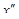 ,у) ³ 0;
,у) ³ 0;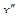 ,у*) ³ 0.
,у*) ³ 0.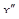 употребляются с вероятностями р и 1-р, где р находится из уравнения
употребляются с вероятностями р и 1-р, где р находится из уравнения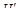 y(
y(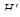 y(
y(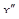 ,у*) =0.
,у*) =0.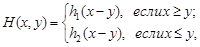
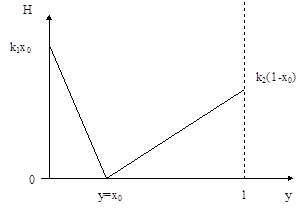
 .
. .
. выделен на рис.4.2. жирной ломаной.
выделен на рис.4.2. жирной ломаной.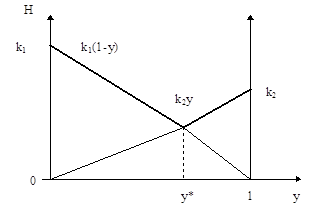
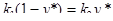 , т.е. при
, т.е. при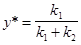 . (4.1)
. (4.1)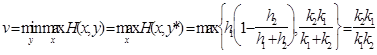 . (4.2)
. (4.2) и
и 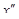 . Для этих стратегий
. Для этих стратегий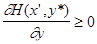 и
и 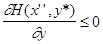 . (4.3)
. (4.3) употребляются с вероятностями р и (1-р), где р находится из уравнения
употребляются с вероятностями р и (1-р), где р находится из уравнения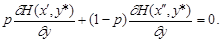 (4.4)
(4.4)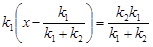 .
.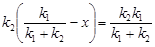 .
.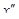 =1.Поэтому игрок 1 должен применять смешанную стратегию, являющуюся смесью этих двух активных стратегий. Для нахождения вероятности р, используем уравнение (4.4).
=1.Поэтому игрок 1 должен применять смешанную стратегию, являющуюся смесью этих двух активных стратегий. Для нахождения вероятности р, используем уравнение (4.4).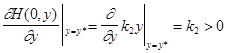 .
.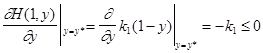 .
.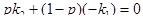 , откуда
, откуда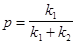 . (4.5)
. (4.5)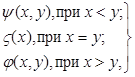 (4.6)
(4.6)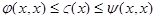 .
.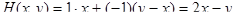 . (4.10)
. (4.10)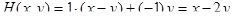 . (4.11)
. (4.11)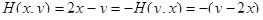 .
.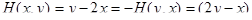 .
.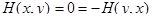 .
.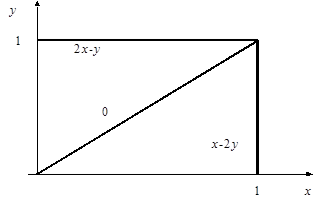
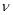 = 0, а оптимальные стратегии игроков 1 и 2 совпадают.
= 0, а оптимальные стратегии игроков 1 и 2 совпадают.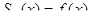 ;
;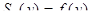 .
.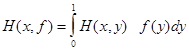 .
.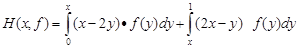 . (4.12)
. (4.12)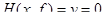 и постоянна, то все производные по х функции Н(x,f) также должны обращаться в нуль.
и постоянна, то все производные по х функции Н(x,f) также должны обращаться в нуль. (4.13)
(4.13)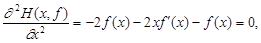 т.е.
т.е. 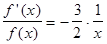 .
.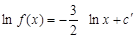 ,
,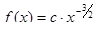 . (4.14)
. (4.14)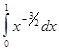 расходится. Следовательно, плотность f не может быть дифференцируемой и больше нуля на всем сегменте [0,1].
расходится. Следовательно, плотность f не может быть дифференцируемой и больше нуля на всем сегменте [0,1].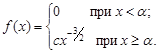
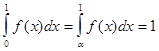 . (4.15)
. (4.15)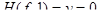 . (4.16)
. (4.16)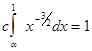 , т.е.
, т.е.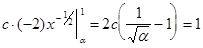 . (4.17)
. (4.17)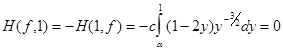 .
.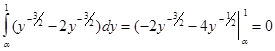 .
.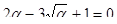 . Это квадратное уравнение имеет два корня: 1 и
. Это квадратное уравнение имеет два корня: 1 и 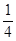 . Корень a=1 противоречит равенству (4.17), а подстановка
. Корень a=1 противоречит равенству (4.17), а подстановка 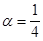 в это равенство дает
в это равенство дает 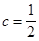 .
.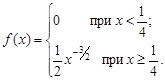
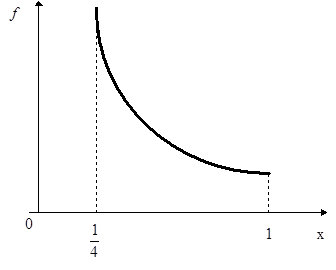
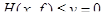 .
.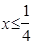 ,
, 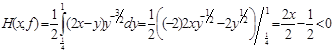 ,
,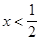 . При
. При 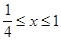 , формула (4.13) дает
, формула (4.13) дает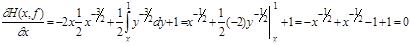 .
.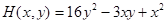 ;
;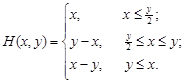
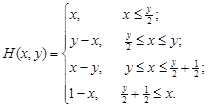
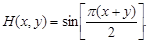
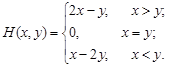
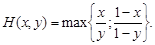
 , с функцией выигрыша Нi(x),
, с функцией выигрыша Нi(x), 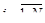 , где x ÎC – ситуация, задаваемая на множество C декартового произведения стратегий Cі.
, где x ÎC – ситуация, задаваемая на множество C декартового произведения стратегий Cі.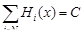 , для всех ситуаций x ÎC.
, для всех ситуаций x ÎC.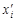
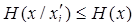 , (5.1)
, (5.1) и
и 
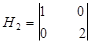 ,
,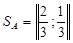 ;
; 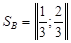 с ценой игры для обоих игроков
с ценой игры для обоих игроков 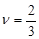 .
.


