Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Абрамченко Н.В. Мещеряков Е.А. Мещерякова Н.А. Ультан А.Е.Стр 1 из 15Следующая ⇒
Абрамченко Н.В. Мещеряков Е.А. Мещерякова Н.А. Ультан А.Е. Реализация математических методов и моделей в MS Excel. Часть II. Учебное пособие
Омск 2019 УДК 004.652 ББК 32.973.26 – 018.2
Рецензенты: д. пед н., профессор, зав. кафедрой «Информационная безопасность» Сибирской автомобильно-дорожной академии Семенова З.В. к. пед. н., доцент, доцент кафедры «Информационная безопасность» Сибирской автомобильно-дорожной академии Анацкая А.Г.
Абрамченко Н.В., Мещеряков Е.А., Мещерякова Н.А., Ультан А.Е. Прикладные экономические задачи в MS Excel. Компьютерный практикум: Учебное пособие – Омск: Издательский центр КАН, 2019. – 80 c.
ISBN
Учебное пособие предназначено для студентов направлений подготовки "Менеджмент" и "Экономика", обучающихся по программам бакалавриата в рамках изучения дисциплин "Математика", "Компьютерный практикум". В пособии рассматриваются вопросы использования MS Excel для решения математических задач, нацеленные на формирование у студентов с помощью компьютерных вычислений практических навыков по реализации математических методов и моделей, применяемых в профессиональных задачах. Пособие может быть полезно всем желающим использовать компьютерные модели для решения расчетных и финансовых задач в практической деятельности. Рекомендовано Учебно-методическим советом Омского филиала Финуниверситета в качестве учебного пособия по дисциплинам "Математика", "Компьютерный практикум", для студентов, обучающихся по направлениям 38.03.02 "Менеджмент", 38.03.01 "Экономика", (программы подготовки бакалавров). Протокол от 24 января 2019 г. № 1.
УДК 004.652 ББК 32.973.26 – 018.2 ISBN
© Абрамченко Н.В., 2019 © Мещеряков Е.А., 2019 © Мещерякова Н.А., 2019 © Ультан А.Е., 2019 СОДЕРЖАНИЕ Введение.. 4 Тема 1....... Нахождение глобальных экстремумов функции (4 ЧАСа)… 5 Тема 2.... исследование числовых характеристик функции (4 часа)… 14 Тема 3. Решение прикладных экономических задач: предельные величины в микроэкономике (4 час.) 22 Тема 4......... Закон убывающей эффективности производства (применение производной) 27 Тема 5. Встроенные функции (продолжение) Решение систем линейных уравнений (4 часа). 30 Тема 6.................... Прикладные задачи оптимизации. Линейное программирование (10 час.) 45
Тема 7... Нелинейное программирование и его применение в экономике.. 66 Тема 8.......................... Встроенные финансовые функции (8 час.) 75 СПИСОК ЛИТЕРАТУРЫ И ССЫЛКИ НА РЕСУРСЫ ИНТЕРНЕТ.. 87 Введение Учебное пособие является продолжением учебного пособия «Финансово-экономические вычисления в MS Excel. Компьютерный практикум» и предназначено для создания прикладной основы использования математического аппарата средствами вычислительных компьютерных технологий, формирования у студентов знаний о вычислительных методах реализации математических объектов и моделей, используемых в экономике и финансах, а также о средствах визуализации математических результатов исследований. Рассматриваются вопросы формирования у студентов практических навыков по использованию компьютерных технологий в вычислительных задачах экономики и финансов. Особенностью Excel является возможность применения формул для описания связи между значениями различных ячеек. Расчет по заданным формулам выполняется автоматически. Изменение содержимого ячейки приводит пересчету значений всех ячеек, которые с ней связаны формульными отношениями, к обновлению всей таблицы в соответствии с изменившимися данными. Применение Excel упрощает работу с данными и позволяет получать результаты без проведения расчетов вручную или специального программирования. Excel можно эффективно использовать для: - проведения расчетов над большими наборами данных; - автоматизации итоговых вычислений; - табулирования функций; - решения задач путём подбора значений параметров; - проведения поиска оптимальных значений параметров; - обработки результатов экспериментов; - построения диаграмм и графиков по имеющимся данным. Пособие содержит расчетные задачи, которые часто приходится решать студентам в процессе обучения при выполнении лабораторных работ, домашних заданий, курсовых и выпускных квалификационных работ. Каждый раздел учебного пособия начинается с изложения теоретического материала в очень ограниченных объемах и решения конкретных задач соответствующей тематики. В конце раздела предлагаются задачи для самостоятельного решения. Некоторые задачи заимствованы из литературных источников, приведенных в списке литературы.
Тема 1. Тема 1. Нахождение глобальных экстремумов функции (4 ЧАСа) Матричные функции Матричные функции используют для решения систем уравнений размерности n x n, т.е. когда число уравнений в системе равно числу неизвестных: функция МОПРЕД(массив) возвращает определитель матрицы; функция МОБР(массив) служит для нахождения обратной матрицы; функция МУМНОЖ(массив1; массив2) возвращает произведение матриц. Для нахождения определителя матрицы выделите свободную ячейку, вызовите встроенную функцию МОПРЕД, где в качестве массива укажите диапазон ячеек с исходной матрицей, нажмите ОК. Результат вычисления появится в выделенной ячейке. Для нахождения обратной матрицы выделите пустой диапазон такого же размера, как и исходная матрица, вызовите функцию МОБР, где в качестве массива укажите диапазон ячеек с исходной матрицей, нажмите сочетание клавиш Shift+Ctrl+Enter. В выделенном диапазоне отобразится обратная матрица. Нахождение произведения матрицы А на матрицу В возможно, если число столбцов матрицы А равно числу строк матрицы В. Для нахождения произведения матриц выделите пустой диапазон такого же размера, как и исходная матрица В, вызовите функцию МУМНОЖ, где в качестве массива1 укажите диапазон ячеек с исходной матрицей А, в качестве массива2 – диапазон ячеек с матрицей В и нажмите сочетание клавиш Shift+Ctrl+Enter. В выделенном диапазоне отобразится результат умножения матриц. Над диапазонами, также как и над числами, можно производить арифметические операции, только в этом случае завершаться операция должна не нажатием клавиши Enter, а нажатием сочетания клавиш Shift+Ctrl+Enter!
Пример 5.3. Используя матричные функции, решите систему уравнений: 2х1 – 2х2 + х3 = 2 х1 + 2х2 + 3х3 = 4 2х1 – 4х2 + 6х3 = 8 Решение. Для решения задачи на листе Excel введем матрицу А и вектор В (рис. 24). В некоторой пустой ячейке (С6) найдем определитель матрицы А, используя встроенную функцию МОПРЕД.
Рис. 24. Исходные данные задачи и определитель матрицы Если определитель матрицы отличен от 0, то система имеет решение. В нашем случае определитель равен 40, т.е. система решение имеет. Найдем это решение. Выделим на листе диапазон пустых ячеек размерности 3х3, например, В8: D 10, вызовем встроенную функцию МОБР, где в качестве массива укажем диапазон ячеек В2: D 4, нажмем сочетание клавиш Shift+Ctrl+Enter. В выделенном диапазоне отобразится обратная матрица. Если Вы не увидели в диапазоне желаемого результата (значение появилось только в одной ячейке, вообще нигде не появилось и др.), нажмите клавишу F2 (в первой ячейке диапазона отобразится =МОБР(B2:D4)), затем Shift+Ctrl+Enter. Если результат опять Вас не устраивает, значит, Вы не выделили диапазон, равный по размерности обратной матрице! Для нахождения вектора Х выделим пустой диапазон ячеек размерности 1х3, например, F 8: F 10, вызовем встроенную функцию МУМНОЖ, где в качестве массива1 укажем диапазон ячеек с обратной матрицей В8: D 10, в качестве массива2 – диапазон ячеек F 2: F 4 с вектором В и нажмем сочетание клавиш Shift+Ctrl+Enter. Результат выполнения задания приведен на рисунке 25. В ячейке F9 отображается число 0 в экспоненциальном формате, указывающем на некоторую погрешность вычислений.
Рис. 25. Решение системы линейных уравнений Пример 5.4. Решите систему уравнений методом Крамера 2х1 – 2х2 + х3 = 2 х1 + 2х2 + 3х3 = 4 2х1 – 4х2 + 6х3 = 8 Решение. Решим ту же систему, что и в предыдущем примере, методом Крамера, и сравним полученные решения. Для этого на листе Excel скопируем и вставим в свободные диапазоны три раза матрицу А (рис. 26). Последовательно заменим столбцы этих матриц на вектор свободных членов: в первой матрице – первый столбец, во второй матрице – второй столбец, в третьей – третий. В ячейках К12:К14 найдем определители полученных матриц, используя встроенную функцию МОПРЕД. Далее в ячейках G 8: G 10 найдем отношения частных определителей к общему (рис. 26). Полученные разными способами решения совпадают.
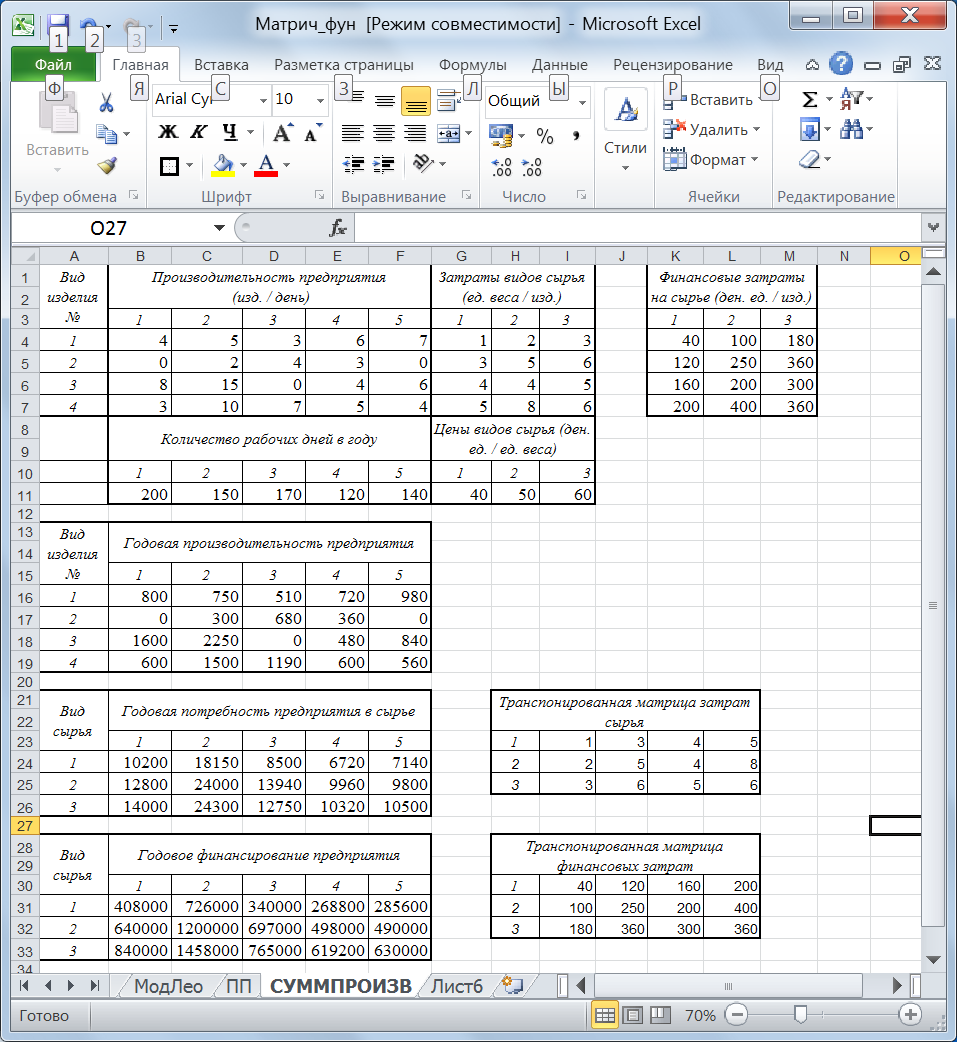
Рис. 26. Исходные данные задачи и определитель матрицы Пример 5.7. В таблице приведены данные о дневной производительности пяти предприятий холдинга, выпускающих четыре вида продукции с использованием трех видов сырья, а также продолжительность работы каждого предприятия в году и цена каждого вида сырья. Таблица 9.
Требуется определить: годовую производительность каждого предприятия по каждому виду изделий; годовую потребность каждого предприятия в каждом виде сырья; годовую сумму финансирования каждого предприятия холдинга для закупки сырья, необходимого для выпуска продукции. Решение. Перенесем исходные данные на лист Excel. Компьютерная модель задачи имеет вид (рис. 31). Для расчета годовой производительности каждого предприятия необходимо найти произведение количества произведенных изделий в день каждым предприятием на количество рабочих дней в году каждого предприятия. Для этого выделим весь диапазон В16: F 19 и введем формулу: =B4:F7*B11:F11, закончив ее ввод сочетанием клавиш Shift+Ctrl+Enter.
Рис. 31. Компьютерная модель примера 5.5. Аналогично рассчитаем матрицу финансовых затрат на каждый вид сырья для каждого изделия (диапазон (K 4:М7): {=G4:I7*G11:I11}).
Для расчета годовой потребности каждого предприятия в каждом виде сырья необходимо найти сумму произведений годового выпуска каждого изделия на затраты каждого вида сырья на единицу изделия. Для этого транспонируем матрицу затрат видов сырья. Для первого изделия в диапазоне В24:В26 найдем произведение полученной транспонированной матрицы (диапазон I 23: L 25) на вектор годовой производительности первого предприятия (диапазон В16:В19). Формулу скопируем вправо для расчета годовой потребности в сырье других предприятий (в диалоговом окне функции МУМНОЖ не забудьте закрепить общий для всех диапазон I 23: L 25!). Аналогично рассчитаем годовое финансирование для каждого предприятия на закупку сырья предварительно транспонировав в диапазоне I 30: L 32 матрицу финансовых затрат на сырье (диапазон К4:М7). Результаты всех расчетов приведены на рисунке 31. Пример 5.8. Известно, что рациональное функционирование многоотраслевого хозяйства предполагает соблюдение баланса между отраслями. Каждая отрасль многоотраслевого хозяйства является, с одной стороны, производителем определенной продукции, а с другой – потребителем продукции, выпускаемой другими отраслями. Макроэкономика функционирования многоотраслевого хозяйства требует, чтобы соблюдался баланс по производству и потреблению между отдельными отраслями. Балансовый принцип связи различных отраслей состоит в том, что валовой выпуск i-й отрасли должен быть равен сумме объемов потребления. В простейшей форме балансовые соотношения имеют вид: xi = xi 1 + xi 2 + … + xi n + yi, i = 1, 2, …, n, где xi — общий объем выпускаемой продукции i -й отрасли; xij — объем продукции i -й отрасли, потребляемый j -й отраслью при производстве объема продукции xj; yi — объем продукции i-й отрасли конечного потребления (для реализации в непроизводственной сфере). Сюда относятся личное потребление граждан, удовлетворение общественных потребностей, содержание государственных институтов и т.д. Для производства продукции j -й отрасли объемом xi нужно использовать продукцию i -й отрасли объемом aijxi, где аij — постоянное число, характеризующее прямые затраты. Это допущение позволяет представить модель многоотраслевой экономики (модель Леонтьева) в виде системы линейных уравнений, которая в матричной форме имеет вид Х = AХ + Y, (А= П / XT, П{Хij} –матрица потребления, т.е. aij = Хij / Х i), где X — вектор валового выпуска; Y — вектор объема продукции конечного потребления; A — матрица прямых затрат. Приведенная система уравнений может быть представлена в виде (E – A) X = Y, где E — единичная матрица. Если существует обратная матрица (E – A)–1 (матрица полных затрат), то существует единственное решение системы X = (E – A)–1 Y. В таблице приведены данные об исполнении баланса за отчетный период (у.е.): Таблица 10.
Вычислить необходимый объем валового выпуска каждой отрасли, если конечное потребление I-ой отрасли увеличится вдвое, а II-ой сохранится на прежнем уровне.
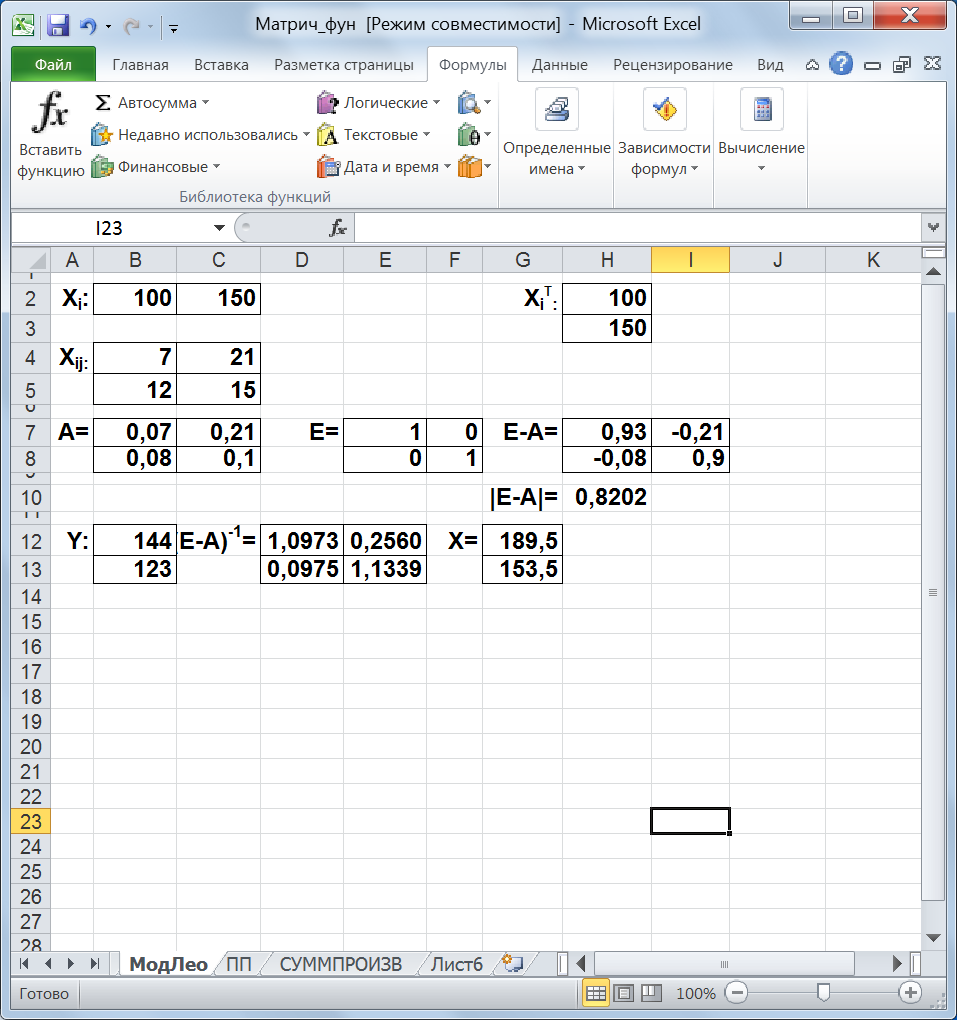
Решение. На лист Excel введем данные для вектор X i, матриц X i j, Е, новый вектор Y, а также свободные диапазоны для матриц X i T, А, (E-A), (E-A) -1 и результирующего вектора Х (рис. 33). Рассчитаем матрицы X i T, А и Е-А по формулам, представленным на рисунке 32. Определитель матрицы | Е-А | = 0,8202 ≠ 0, так что обратная матрица и решение указанной системы уравнений существуют. Найдем его с использованием встроенных функций МОБР и МУМНОЖ (рис. 33). Таким образом, согласно рис. 33, в I-ой отрасли валовой выпуск надо увеличить до 189,5 у.е., а во II-ой — до 153,5 у.е.
Рис. 32. Формулы расчетов матриц А и Е-А
Рис. 33. Решение балансовых экономических моделей Задания для самостоятельного выполнения Задание 5.1 Предприятие ежесуточно выпускает четыре вида изделий, производственно-экономические показатели которых приведены в таблице: Таблица 11.
Требуется определить следующие ежесуточные показатели: расход сырья S, затраты рабочего времени Т и стоимость Р выпускаемой продукции предприятия.
Задание 5.2. Найти произведение матриц: 1)
3)
Задание 5.3 Используя операции с матрицами, решите систему уравнений: х1 + 2х2 + 8х3 + 22 = 0 х1 – х2 + х3 + 2,5 = 0 10х1 – 3х2 – 19 = 0 Задание 5.4 Решите систему уравнений методом Крамера: 5х1 + 3х2 – х3 = 8 2х1 – 4х2 + 3х3 = 3 7х1 + 4х2 – 2х3 = 9
Задание 5.5 Решите систему уравнений методом наименьших квадратов: 8х1 + 5х2 = 10 5х1 + 2х2 = 4 7х1 + 4х2 = 8
Задание 5.6. Ресторан специализируется на выпуске трех видов фирменных блюд: В1, В2, ВЗ, при этом используются ингредиенты трех типов S1, S2, S3. Нормы расхода каждого из них на одно блюдо и объем расхода ингредиентов на 1 день заданы таблице 12. Найти расход каждого ингредиента, если выпускается по 250 единиц каждого блюда. Хватит ли имеющихся запасов? Таблица 12.
Задание 5.7. В таблице приведены данные по балансу за некоторый период времени между пятью отраслями. Таблица 13.
Требуется найти векторы конечного потребления и валового выпуска, а также матрицу коэффициентов прямых затрат и определить ее продуктивность. В приведенной таблице в первых пяти столбцах (группа “Потребление”) содержатся значения xij, в последнем столбце содержатся элементы вектора валового выпуска x, в предпоследнем столбце – элементы вектора объема конечного потребления y. Задание 5.8. В таблице приведены данные по балансу за некоторый период времени между тремя отраслями. Таблица 14.
Требуется найти объем валового выпуска каждого вида продукции, если конечное потребление по отраслям увеличить, соответственно, до 60, 70 и 30 условных денежных единиц. III | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Виды работ | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Производительность механизмов м3/ч | 20 | 15 | 16 | 30 | 14 | 18 | 35 | 32 | 15 | 29 | 40 | 15 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Себестоимость 1 ч работы д.е. | 2 | 5 | 3 | 6 | 2 | 4 | 5 | 7 | 8 | 3 | 6 | 3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Задание 6.10. В регионе располагаются хранилища ГСМ и центры их распределения. Доставка ГСМ от хранилищ к центрам распределения осуществляется периодически или по заявкам автомобильным транспортом.
Исходные данные о емкости хранилищ и центров распределения, а также о среднем времени доставки ГСМ от хранилищ к центрам распределения представлены в нижеследующей таблице.
Таблица 23.
| Центры распред. ГСМ | Хранилища ГСМ | Емкость центров распред. | |||
| Хранил. 1 | Хранил. 2 | Хранил. 3 | Хранил. 4 | ||
| Центр1 | 0,5 | 1,2 | 1,0 | 0,8 | 300 |
| Центр2 | 1,0 | 1,1 | 0,6 | 1,4 | 270 |
| Центр3 | 0,6 | 1,2 | 2,0 | 1,0 | 350 |
| Центр4 | 0,8 | 1,5 | 0,9 | 1,4 | 550 |
| Центр5 | 1,2 | 1,8 | 1,6 | 1,4 | 600 |
| Центр6 | 0,7 | 1,2 | 0,3 | 0,5 | 420 |
| Центр7 | 0,2 | 1,4 | 0,4 | 1,0 | 750 |
| Центр8 | 1,2 | 1,0 | 0,6 | 0,6 | 560 |
| Центр9 | 0,4 | 0,5 | 1,7 | 1,2 | 860 |
| Центр10 | 0,9 | 1,0 | 0,8 | 1,3 | 580 |
| Емкость хранилищ ГСМ | 1400 | 1200 | 1600 | 1400 | |
Требуется разработать такой план прикрепления центров распределения к хранилищам ГСМ, чтобы общее время доставки ГСМ было минимальным.
Задание 6.11. В городе есть два склада телевизоров и два магазина. Необходимо ежедневно с первого склада вывозить 50 телевизоров, а со второго – 70. Первый магазин при этом получает 40 телевизоров, а второй – 80. Магазины и склады расположены в разных районах города, в связи с чем перевозки со складов в магазины зависят от расстояния и равны соответственно: со Склада№1 в Магазин№1 – 650 руб., со Склада№2 в Магазин№1 – 730 руб., со Склада№1 в Магазин№2 – 740 руб., со Склада№2 в Магазин№2 – 880 руб. Спрашивается, как нужно организовать работу транспорта, чтобы затраты на перевозку были минимальными.
Задание 6.12.
| 5 4 1 2 4 2 5 3 7 3 5 4 |
Задание 6.13. Предприятие планирует выпускать пять видов изделий различной прибыльности, для изготовления каждого из которых необходима обработка на четырех станках. Общее время эксплуатации каждого станка в сутки ограничено условиями эксплуатации. Число рабочих дней в месяце равно 25.
С учетом исходных данных, приведенных в таблице ниже и обеспечения максимальной месячной прибыли определить, какие изделия, в каком количестве должно выпускать предприятие?
Таблица 24.
| Изделие | Прибыль, руб | Время обработки изделия, час | |||
| Станок1 | Станок2 | Станок3 | Станок4 | ||
| Изделие1 | 150 | 3 | 5 | 4 | 4 |
| Изделие2 | 200 | 2 | 1 | 4 | 2 |
| Изделие3 | 300 | 4 | 3 | 3 | 2 |
| Изделие4 | 100 | 5 | 4 | 3 | 5 |
| Изделие5 | 400 | 2 | 2 | 5 | 3 |
| Максимальное время работы станка в сутки, час | 16 | 15 | 19 | 15 | |
Задание 6.14. Из двух сортов бензина образуются две смеси – А и В. Смесь А содержит 60 % 1 -го сорта и 40 % 2 -го сорта бензина; смесь В – 80 % 1 -го сорта и 20 % 2 -го сорта. Цена 1 кг смеси А – 10 ден. ед., а смеси В – 12 ден. ед.
Составьте план образования смесей, при котором будет получен максимальный доход, если в наличии имеется бензин 50 тонн 1 -го сорта и 30 тонн второго сорта.
Задание 6.15. Пункт B находится на расстоянии 60 км от железной дороги. Расстояние по железной дороге от пункта A до ближайшей к пункту B точки C составляет 285 км. На каком расстоянии от точки C надо построить станцию, чтобы затрачивать наименьшее время на передвижение между пунктами A и B, если скорость движения по железной дороге равна 52 км/ч, а скорость движения по шоссе равна 20 км/ч?
Задание 6.16. Необходимо составить оптимальный план производства красок с учетом ограничений на ресурсы и потребностей в готовой продукции.
Цех выпускает два вида красок: для внутренних (обозначим ее через I) и наружных работ (E). Продукция обоих видов поступает в оптовую продажу. Для производства красок используются два исходных продукта (сырье) – А («суспензия в пентафталевом лаке») и В («органический растворитель и специальные добавки»). Максимально возможные суточные запасы этих продуктов, расходы на 1 т. соответствующих красок и оптовые цены одной тонны красок приведены в таблице 20.
Таблица 25.
Ограничения для задачи о производстве красок
| Исходный продукт | Расход исходных продуктов (в тоннах) на тонну краски | Максимально возможный запас, т | |
| краска Е | краска I | ||
| А | 1 | 2 | 6 |
| В | 2 | 1 | 8 |
| Спрос | 2 | ||
| Цена (тыс.р.) | 66 | 60 | |
Изучение рынка сбыта показало, что суточный спрос на краску I никогда не превышает 2 т. в сутки. Кроме того, установлено, что спрос на краску I никогда не превышает спроса на краску E более чем на 1 т.
Пример 6.17. Рассматриваемая нами компания производит пять видов игрушек, для которых используются 6 видов материала в различных количествах.
Входные данные представлены в таблице.
Таблица 26.
| A | B | C | D | E | F | G | |
| 2 | Необходимые материалы | ||||||
| 3 | Материал | Игрушка A | Игрушка B | Игрушка C | Игрушка D | Игрушка E | Запас |
| 4 | Красная краска | 0 | 1 | 0 | 1 | 3 | 625 |
| 5 | Голубая краска | 3 | 1 | 0 | 1 | 0 | 640 |
| 6 | Белая краска | 2 | 1 | 2 | 0 | 2 | 1100 |
| 7 | Пластик | 1 | 5 | 2 | 2 | 1 | 875 |
| 8 | Дерево | 3 | 0 | 3 | 5 | 5 | 2200 |
| 9 | Клей | 1 | 2 | 3 | 2 | 3 | 1500 |
| 10 | Доход на единицу | 150 | 300 | 200 | 250 | 250 | |
| 11 | План выпуска | 186 | 18 | 165 | 40 | 189 | |
Решение.
Спрос на болты по условию задачи известный и постоянный, следовательно, мы можем без ограничений использовать модель экономичного размера заказа EOQ. При этом все издержки будут определяться полными издержками хранения и заказа за год. Однако имеется система скидок на базовые цены, а это значит, что отклонение от экономичного размера заказа может оказаться выгодным, если полученные скидки превышают рост издержек хранения. Значит к сумме издержек хранения и заказа нужно добавить общие затраты на покупку болтов, чтобы иметь возможность корректно сравнивать разные предложения.
Так как в данной задаче нам необходимо рассчитать оптимальный заказ для шести цен и количественных диапазонов (2 поставщика и 3 диапазона действия цен у каждого) организуем данные, как показано в таблице (Рис. 49).
| A | B | C | D | E | F | G | |
| 1 | h | S | D | ||||
| 2 | 38% | 1000 | 50000 | ||||
| 3 | Поставщик A | Поставщик B | |||||
| 4 | Порог скидки, макс. | 4 999 | 19 999 | 1 000 000 | 9 999 | 29 999 | 1 000 000 |
| 5 | Мин. | 1 | 5 000 | 20 000 | 1 | 10 000 | 30 000 |
| 6 | Цена | 5 | 4.6 | 4.4 | 4.8 | 4.5 | 4.3 |
| 7 | EOQ | =КОРЕНЬ(2*$C$2*$B$2/(B6*$A$2)) | |||||
| 8 | Реальный Q | =ЕСЛИ(И(B7>=B5;B7<=B4);B7;ЕСЛИ(B7<B5;B5;B4)) | |||||
| 9 | TH | =B8/2*$A$2*B6 | |||||
| 10 | TS | =$C$2/B8*$B$2 | |||||
| 11 | T | =B10+B9 | |||||
| 12 | Т+ТС | =B11+$C$2*B6 | |||||
Рис. 49. Компьютерная модель задачи об оптимальном размере заказа
В верхних ячейках A 2: C 2 запишем общие данные: издержки хранения, издержки заказа и годовую потребность. В строках B 4: G 4 и B 5: G 5 запишем верхние и нижние границы диапазонов скидок. Число 1 млн. в ячейках D 4 и G 4 заменяет бесконечную границу диапазона и выбрано произвольно, для упрощения формул.
Для расчета экономичного размера заказа используем стандартную формулу  . В нашей задаче величина H непостоянна, так как она зависит от цены товара, а цена может быть разной. Поэтому в расчетах вместо самой величины H будем использовать ее выражение через цену и издержки хранения в процентах h: H = h * C. С этой поправкой формула для EOQ и записана в ячейке B 7. Ссылки на издержки хранения h, годовую потребность D и издержки заказа S фиксированы, для удобства протягивания формулы вправо, для расчета EOQ для других цен закупки. После протягивания формулы получаем следующий результат (таблица 30).
. В нашей задаче величина H непостоянна, так как она зависит от цены товара, а цена может быть разной. Поэтому в расчетах вместо самой величины H будем использовать ее выражение через цену и издержки хранения в процентах h: H = h * C. С этой поправкой формула для EOQ и записана в ячейке B 7. Ссылки на издержки хранения h, годовую потребность D и издержки заказа S фиксированы, для удобства протягивания формулы вправо, для расчета EOQ для других цен закупки. После протягивания формулы получаем следующий результат (таблица 30).
Если мы теперь сравним полученные значения EOQ с диапазонами количеств закупаемых болтов, для которых действуют те цены, по которым мы считали EOQ, то обнаружим несколько несоответствий.
Таблица 30
| Порог скидки, макс. | 4 999 | 19 999 | 1 000 000 | 9 999 | 29 999 | 1 000 000 |
| мин. | 1 | 5 000 | 20 000 | 1 | 10 000 | 30 000 |
| Цена | 5 | 4.6 | 4.4 | 4.8 | 4.5 | 4.3 |
| EOQ | 7 254.8 | 7 563.6 | 7 733.6 | 7 404.4 | 7 647.2 | 7 823.0 |
Например, при покупке болтов у поставщика A по цене 5 руб. за штуку оптимальная величина заказа равна примерно 7255 штук. Но такая цена действует только при покупке менее 5000 штук. Если мы будем закупать болты партиями по 7255 штук, то их цена будет только 4,6 руб. Это конечно неплохо, но мы ведь хотели выяснить, какую партию болтов лучше всего выбрать, если покупать их по цене 5 руб.!
Ясно, что выбирать размер партии мы должны только внутри диапазона от 1 до 5000 штук. Какой же размер выбрать? Здесь нужно вспомнить, как выглядит график зависимости суммы издержек хранения и заказа от размера заказа. А именно, график этот показывает гладкую функцию без перегибов с одним минимумом. Это значит, что чем ближе размер заказа к EOQ, тем меньше издержки и наоборот. Следовательно, в тех случаях, когда мы не можем выбрать размер заказа равным EOQ, мы должны взять реально возможную величину заказа, наиболее близкую к экономичному размеру заказа.
В случае с покупкой болтов по цене 5 руб. – это верхняя граница диапазона, т.е. 4999 штук.
Поэтому в таблицу 30 кроме строки для расчета EOQ добавлена строка “Реальный Q ” – реальный размер заказа (таблица 31). В этой строке мы будем записывать тот размер заказа, который выбираем на самом деле. Конечно, в жизни мы можем выбирать реальный размер заказа, отличный от теоретически оптимального не только из-за диапазонов действия цен. Скажем, во втором столбце EOQ равен 7563,6 и попадает в диапазон действия цены 4,6 руб. – от 5000 до 19999. Но не можем же мы заказать дробное число болтов! Значит, как минимум надо выбрать реальный размер заказа, как округленное до целых значение EOQ. Кроме того, часто бывает, что штучный товар фасуется в стандартную тару. В этом случае нужно заказывать партию так, чтобы получалось целое число коробок или ящиков и т.п. Могут быть и другие причины, заставляющие отклоняться от теоретической величины оптимального заказа. Поэтому не существует никакой стандартной формулы для реального Q.
В сложных случаях реальный Q можно проставить вручную с учетом известных вам условий. А в нашей задаче можно написать и формулу, так как выбор достаточно прост. Такая формула и записана в ячейке B 8.