
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Непрерывные системы двух случайных величин
Задача 2. Система случайных величин
в треугольной области АВС с координатами А(-1; 0), В(0; 1), С(-1; 2). Требуется: а) вычислить константу а в выражении для плотности вероятности б) вычислить вероятность попадания случайной точки в) найти безусловные плотности вероятности г) найти условные плотности вероятности д) установить, являются ли случайные величины x и h независимыми; е) вычислить основные числовые характеристики системы
ж) найти условные математические ожидания з) построить линии регрессии (x по h и h по x). Решение. Изобразим треугольную область АВС (рис. 2.1). а) Для нахождения константы а в выражении для плотности вероятности
Имеем
и, следовательно,
Напоминание. Площадь треугольника, построенного на векторах
Рис. 2.1 б) Вероятность попадания равномерно распределенной в области D случайной точки
Точка D(0; 4)
в) Зная совместную плотность вероятности
Для расстановки пределов интегрирования в последних формулах составим уравнения прямых АВ, ВС и АС. Напоминания: 1. Уравнение прямой, проходящей через две точки
2. Уравнение прямой в отрезках имеет вид
где а - абсцисса точки пересечения прямой с осью Ох, b - ордината точки пересечения прямой с осью Оу. Уравнение прямой АВ имеет вид:
Уравнение прямой ВС имеет вид:
Уравнение прямой АС: Треугольник АВС не является областью, стандартной относительно оси Таким образом,
Итак,
Плотность вероятности
Для его проверки построим график
Рис. 2.2
Площадь треугольника, ограниченного графиком Треугольник АВС является областью, стандартной относительно оси Ох (см. рис. 2.1). Линия входа - отрезок оси Оу ( Таким образом,
Итак, Для проверки условия нормировки
Рис. 2.3
Согласно рис. 2.3 площадь треугольника, ограниченного графиком г) Условные плотности вероятности выражаются через безусловные по формулам:
Следовательно,
Заметим, что условие нормировки д) Установить зависимость или независимость случайных величин x и h, входящих в систему е) Вычислим основные числовые характеристики системы
Заметим, что если система случайных величин
(
Проверим:
Для вычисления дисперсии
Вычислим второй начальный момент
Тогда
Аналогично вычислим дисперсию случайной величины h:
Корреляционный момент
Для этого вычислим сначала второй смешанный начальный момент
Тогда
Безразмерной характеристикой связи между случайными величинами x и h служит коэффициент корреляции
В рассматриваемом случае
Коэффициент корреляции
ж) Условные математические ожидания случайных величин x и h, входящих в систему
Имеем:
Заметим, что в случае равномерного распределения системы з) Построим линии регрессии, определяемые уравнениями
Графики линий регрессии приведены на рис. 2.4.
Рис. 2.4 Заметим, что линия регрессии
|
||||||
|
Последнее изменение этой страницы: 2020-03-14; просмотров: 149; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.36.141 (0.041 с.) |
 задана совместной плотностью вероятности
задана совместной плотностью вероятности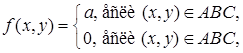
 ;
; и
и  случайных величин x и h;
случайных величин x и h; ,
, 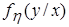 ;
; .
. и
и 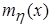 (случайной величины x относительно h и случайной величины h относительно x);
(случайной величины x относительно h и случайной величины h относительно x); , воспользуемся условием нормировки
, воспользуемся условием нормировки
 ,
, .
. и
и  , равна
, равна


 , найдем по формуле:
, найдем по формуле: .
. (см. рис. 2.1), следовательно,
(см. рис. 2.1), следовательно, .
.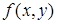 , можно найти безусловную плотность вероятности любой из случайных величин, входящих в систему
, можно найти безусловную плотность вероятности любой из случайных величин, входящих в систему  по формулам:
по формулам: ,
, =
=  .
. и
и  , имеет вид
, имеет вид
 ,
,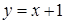 ,
,  .
. ,
,  .
. .
. (см. рис. 2.1). Линия входа - отрезок прямой АВ (
(см. рис. 2.1). Линия входа - отрезок прямой АВ ( .
. =
= 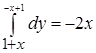 , если
, если  =
= 
 .
.
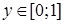 , и отрезок прямой ВС (
, и отрезок прямой ВС ( =
=  , если
, если  , если
, если  .
.
 построим график
построим график  (рис. 2.3).
(рис. 2.3).
 =
= 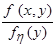 при
при  ,
, =
=  при
при 
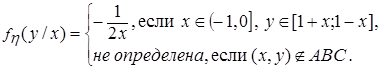
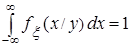 должно выполняться для любого фиксированного у, а условие нормировки
должно выполняться для любого фиксированного у, а условие нормировки  должно выполняться для любого фиксированного х.
должно выполняться для любого фиксированного х. , можно, сравнив условные
, можно, сравнив условные  и безусловные
и безусловные  =
= 
 и
и 

 =
=  ;
; =
= 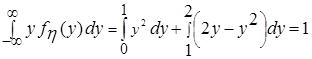 .
.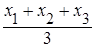 ,
,  ;
; ,
,  =
=  .
. воспользуемся формулой
воспользуемся формулой .
. :
: .
. .
. =
=  .
. , характеризующий связь между случайными величинами x и h, найдем по формуле
, характеризующий связь между случайными величинами x и h, найдем по формуле .
. =
= 


 :
: .
. .
.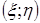 , найдем по формулам:
, найдем по формулам: =
=  и
и  =
= 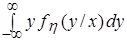 .
. =
= 
 =
= 
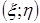 функции
функции  и
и  . В рассматриваемой задаче
. В рассматриваемой задаче ,
,

 графически изображает зависимость «в среднем» случайной величины x от возможных значений случайной величины h. Аналогично для
графически изображает зависимость «в среднем» случайной величины x от возможных значений случайной величины h. Аналогично для 


