Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дискретные системы двух случайных величинСтр 1 из 4Следующая ⇒
Дискретные системы двух случайных величин
Задача 1. По цели производиться два независимых выстрела. Вероятность попадания в цель при первом выстреле равна р1=0.7, при втором р2=0.8. Рассматривается дискретная система двух случайных величин Для рассматриваемой дискретной системы случайных величин а) описать закон распределения системы б) описать законы распределения отдельных случайных величин, входящих в систему; в) описать условный закон распределения случайной величины x при условии h = 1 и при этом условии вычислить условное математическое ожидание г) выяснить, зависимы или нет случайные величины x и h; д) вычислить вероятности е) вычислить основные числовые характеристики для системы
Решение. а) Для описания закона распределения дискретной системы двух случайных величин необходимо определить множество всех возможных пар значений
и соответствующие вероятности
Таблица 2.1
В первой строке указываются возможные значения случайной величины x, а в первом столбце - возможные значения случайной величины h; в последней строке и в последнем столбце указываются безусловные вероятности возможных значений соответственно случайных величин x и h. В каждой клетке таблицы, стоящей на пересечении i-го столбца и j-й строки, указываются вероятности совместного осуществления события
т. е.,
Заполним таблицу.
Занесем полученные данные в табл. 2.2
Таблица 2.2
По условию нормировки
Условие нормировки выполняется. б) Законы распределения отдельных дискретных случайных величин, входящих в систему, получим из закона распределения дискретной системы случайных величин (см. табл. 2.2). Возможные значения случайных величин x и h известны, найдем соответствующие им вероятности. Для случайной величины x вероятности возможных значений определяются по формуле
т.е. суммируем вероятности «по столбцам»:
Аналогично для случайной величины h используем формулу
т.е. суммируем вероятности «по строкам»:
Законы распределения случайных величин x и h представим в виде ряда распределения для каждой величины (табл. 2.3, 2.4).
Таблица 2.3
Таблица 2.4
в) Условным законом распределения случайной величины x при условии, что величина h приняла определенное значение
Условный закон распределения случайной величины x при условии, что величина h приняла значение, равное 1, находим по формуле (1), полагая h =0:
Тогда
Запишем условный закон распределения случайной величины x в виде ряда распределения (табл. 2.5).
Таблица 2.5
Используя данные табл. 2.5 и формулу условного математического ожидания случайной величины x при условии, что величина h приняла определенное значение
вычислим условное математическое ожидание
г) Установить зависимость или независимость случайных величин x и h, входящих в систему
Так как
взять, например,
следовательно, случайные величины x и h независимы. д) Вычислим вероятности
е) Найдем основные числовые характеристики дискретной системы случайных величин x и h. Используя табл. 2.3 и 2.4, найдем
Корреляционный момент вычислим с помощью данных табл. 2.2 и следующей формулы:
Коэффициент корреляции определяется как отношение корреляционного момента к произведению среднеквадратичных отклонений случайных величин x и h:
Так как коэффициент корреляции
Решение. Изобразим треугольную область АВС (рис. 2.1). а) Для нахождения константы а в выражении для плотности вероятности
Имеем
и, следовательно,
Напоминание. Площадь треугольника, построенного на векторах
Рис. 2.1 б) Вероятность попадания равномерно распределенной в области D случайной точки
Точка D(0; 4)
в) Зная совместную плотность вероятности
Для расстановки пределов интегрирования в последних формулах составим уравнения прямых АВ, ВС и АС. Напоминания: 1. Уравнение прямой, проходящей через две точки
2. Уравнение прямой в отрезках имеет вид
где а - абсцисса точки пересечения прямой с осью Ох, b - ордината точки пересечения прямой с осью Оу. Уравнение прямой АВ имеет вид:
Уравнение прямой ВС имеет вид:
Уравнение прямой АС: Треугольник АВС не является областью, стандартной относительно оси Таким образом,
Итак,
Плотность вероятности
Для его проверки построим график
Рис. 2.2
Площадь треугольника, ограниченного графиком Треугольник АВС является областью, стандартной относительно оси Ох (см. рис. 2.1). Линия входа - отрезок оси Оу ( Таким образом,
Итак, Для проверки условия нормировки
Рис. 2.3
Согласно рис. 2.3 площадь треугольника, ограниченного графиком г) Условные плотности вероятности выражаются через безусловные по формулам:
Следовательно,
Заметим, что условие нормировки д) Установить зависимость или независимость случайных величин x и h, входящих в систему е) Вычислим основные числовые характеристики системы
Заметим, что если система случайных величин
(
Проверим:
Для вычисления дисперсии
Вычислим второй начальный момент
Тогда
Аналогично вычислим дисперсию случайной величины h:
Корреляционный момент
Для этого вычислим сначала второй смешанный начальный момент
Тогда
Безразмерной характеристикой связи между случайными величинами x и h служит коэффициент корреляции
В рассматриваемом случае
Коэффициент корреляции ж) Условные математические ожидания случайных величин x и h, входящих в систему
Имеем:
Заметим, что в случае равномерного распределения системы з) Построим линии регрессии, определяемые уравнениями
Графики линий регрессии приведены на рис. 2.4.
Рис. 2.4 Заметим, что линия регрессии Решение. а) Нормальный закон распределения для системы двух случайных величин
где
б) Область
где
Рис 2.5
Область
Рис. 2.6
Следовательно, для вычисления искомой вероятности целесообразно применение формулы
Область
Рис. 2.7
Найдем вероятность попадания в область
Область
Рис. 2.8
Искомую вероятность можно найти, исходя из симметричности поверхности распределения относительно плоскостей
Вероятность попадания случайной точки
где
Рис. 2.9 случайный величина распределение дисперсия в) Для определения вероятности
Затем находим вероятность того, что случайная точка при трех опытах ни разу не попадет в
и, наконец, искомую вероятность:
г) Вероятность
и вероятности попадания случайной точки в область
Итак, искомая вероятность
д) Если событие в каждом опыте может наступить с вероятностью
По условию,
т.е. необходимо провести как минимум 1 опыта.
Решение. а) Функция
Подставив сюда
получим
Таким образом, случайная величина h =
б) Графики функций
Рис. 2.10 Рис. 2.11
Проверим условия нормировки для функций
Имеем:
в) Используя формулу
Однако этот же результат можно получить, применяя формулу
Таким образом,
Итак,
Решение. а) Если функция
Проверим его выполнение:
Строим график функции
Рис. 2.12
Замечание. Опущенные выкладки полного исследования функции б) Способ 1. Для нахождения математического ожидания и дисперсии случайной величины
Учитывая, что
Замечание. Полученный результат Находим дисперсию:
Способ 2. Пользуясь определением математического ожидания функции случайного аргумента, его свойствами и указанными формулами (способ 1), получим:
Аналогично для дисперсии:
Итак,
Решение а) Так как случайная величина x имеет равномерное распределение, а h - нормальное распределение, то их плотности вероятности определяются соответственно выражениями:
Следовательно,
б) Запишем числовые характеристики исходных случайных величин:
Используя свойства математического ожидания и дисперсии функции случайных величин, получим:
Итак, искомые числовые характеристики
в) Зная числовые характеристики исходных случайных величин, пользуясь свойствами и определением математического ожидания функции непрерывной случайной величины, имеем:
=
Таким образом,
Решение Согласно заданной корреляционной матрице имеем:
Искомые числовые характеристики найдем, пользуясь свойствами математического ожидания, дисперсии и корреляционного момента:
а)
Искомые характеристики
б)
=
Таким образом,
Характеристическая функция Задача 8. Для данной плотности вероятности Решение. I способ. Воспользуемся методами операционного исчисления. Так как данная плотность вероятности
II способ. Характеристическую функцию
Вычислим
Решение
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-03-14; просмотров: 125; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.66.196 (0.382 с.) |
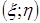 , где x - число попаданий при первом выстреле, h - число попаданий при втором выстреле.
, где x - число попаданий при первом выстреле, h - число попаданий при втором выстреле.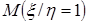 ;
;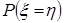 и
и  >h);
>h); .
.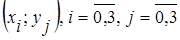
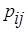 . Результат удобно представить в виде таблицы 2.1
. Результат удобно представить в виде таблицы 2.1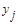
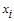 01
01
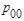
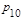
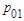
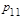
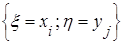 ,
,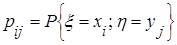
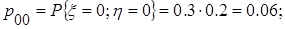
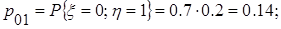
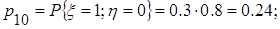
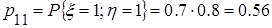

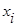 01pj
01pj
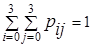 . Сделаем проверку:
. Сделаем проверку: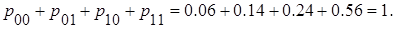
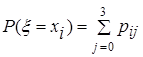 ,
,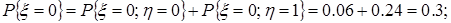
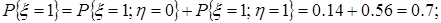
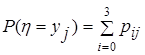 ,
,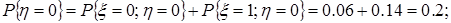
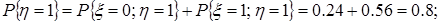
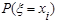 0.30.7
0.30.7
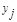 01
01
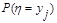 0.20.8
0.20.8
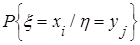 , определяемых по формуле
, определяемых по формуле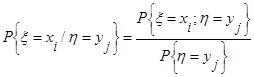 . (1)
. (1)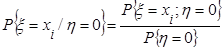 .
.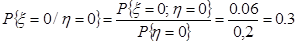
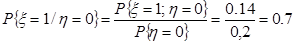
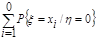
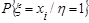 0.30.71
0.30.71
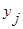 :
:
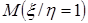 :
: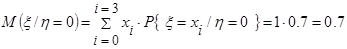
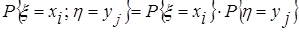 .
.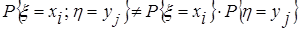 ,
,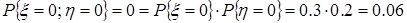
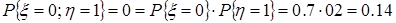
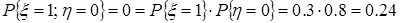
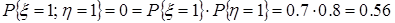
 и
и 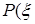 >h):
>h):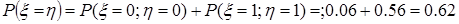
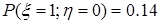
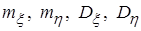 по формулам:
по формулам: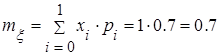
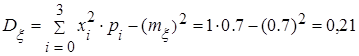
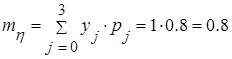
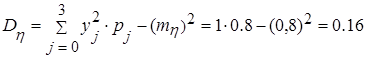
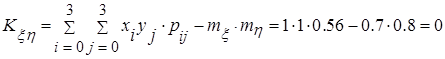
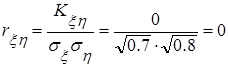
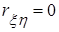 , то можно утверждать, что случайные величины x и h линейно независимы.
, то можно утверждать, что случайные величины x и h линейно независимы. , воспользуемся условием нормировки
, воспользуемся условием нормировки
 ,
, .
. и
и  , равна
, равна


 в некоторую область
в некоторую область  , найдем по формуле:
, найдем по формуле: .
. (см. рис. 2.1), следовательно,
(см. рис. 2.1), следовательно, .
.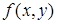 , можно найти безусловную плотность вероятности любой из случайных величин, входящих в систему
, можно найти безусловную плотность вероятности любой из случайных величин, входящих в систему  по формулам:
по формулам: =
=  ,
, =
=  .
. и
и  , имеет вид
, имеет вид
 ,
,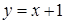 ,
,  .
. ,
,  .
. .
. (см. рис. 2.1). Линия входа - отрезок прямой АВ (
(см. рис. 2.1). Линия входа - отрезок прямой АВ ( .
. =
= 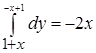 , если
, если  =
= 
 .
.
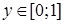 , и отрезок прямой ВС (
, и отрезок прямой ВС ( =
=  , если
, если  , если
, если  .
.
 построим график
построим график  (рис. 2.3).
(рис. 2.3).
 =
= 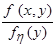 при
при  ,
, =
=  при
при 
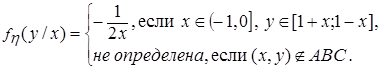
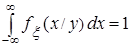 должно выполняться для любого фиксированного у, а условие нормировки
должно выполняться для любого фиксированного у, а условие нормировки  должно выполняться для любого фиксированного х.
должно выполняться для любого фиксированного х. , можно, сравнив условные
, можно, сравнив условные  и безусловные
и безусловные  =
= 
 и
и 

 =
=  ;
; =
= 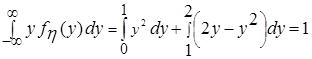 .
.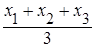 ,
,  ;
; ,
,  =
=  .
. воспользуемся формулой
воспользуемся формулой .
. :
: .
. .
. =
=  .
. , характеризующий связь между случайными величинами x и h, найдем по формуле
, характеризующий связь между случайными величинами x и h, найдем по формуле .
. =
= 


 :
: .
. .
.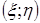 , найдем по формулам:
, найдем по формулам: =
=  и
и  =
= 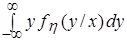 .
. =
= 
 =
= 
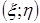 функции
функции  и
и  . В рассматриваемой задаче
. В рассматриваемой задаче ,
,

 графически изображает зависимость «в среднем» случайной величины x от возможных значений случайной величины h. Аналогично для
графически изображает зависимость «в среднем» случайной величины x от возможных значений случайной величины h. Аналогично для 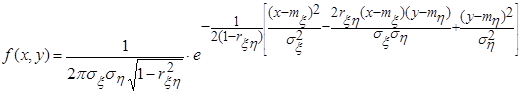 ,
,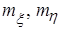 - математические ожидания случайных величин,
- математические ожидания случайных величин, 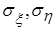 - средние квадратические отклонения,
- средние квадратические отклонения, 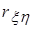 - коэффициент корреляции. Поэтому плотность вероятности данной системы имеет вид
- коэффициент корреляции. Поэтому плотность вероятности данной системы имеет вид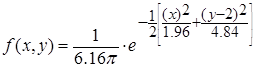 .
.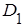 является прямоугольником с осями, параллельными главным осям рассеивания (рис. 2.5). По формуле
является прямоугольником с осями, параллельными главным осям рассеивания (рис. 2.5). По формуле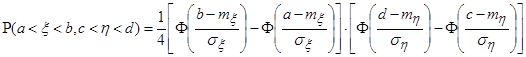 ,
,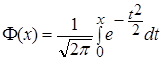 - функция Лапласа, значения которой находятся по таблице, вычисляем вероятность попадания случайной точки
- функция Лапласа, значения которой находятся по таблице, вычисляем вероятность попадания случайной точки 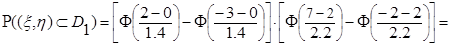
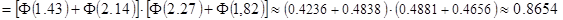
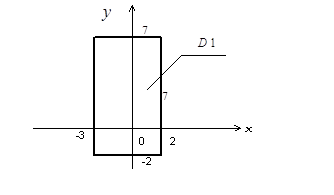
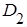 является прямоугольником с осями, параллельными главным осям рассеивания и центром в центре рассеивания (рис. 2.6).
является прямоугольником с осями, параллельными главным осям рассеивания и центром в центре рассеивания (рис. 2.6).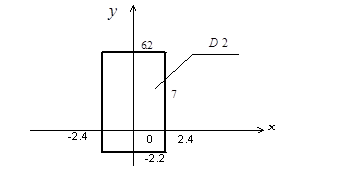
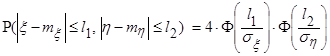
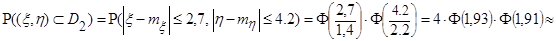
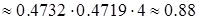
 является квадрантом с вершиной в точке (-3-2) (рис.2.7).
является квадрантом с вершиной в точке (-3-2) (рис.2.7).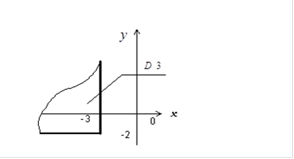
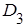 :
: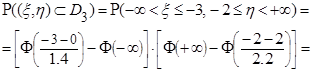
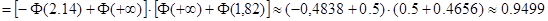 .
.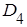 является квадрантом с вершиной в центре рассеивания
является квадрантом с вершиной в центре рассеивания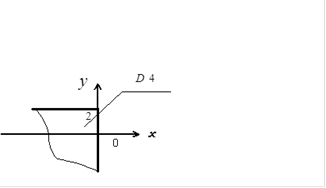
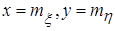 :
: .
.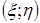 в эллипс рассеивания
в эллипс рассеивания 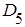 (рис.2.9) вычисляем по соответствующей формуле:
(рис.2.9) вычисляем по соответствующей формуле: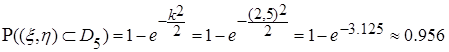 ,
,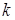 - размеры полуосей эллипса рассеивания в единицах среднего квадратического отклонения по направлению главных осей рассеивания.
- размеры полуосей эллипса рассеивания в единицах среднего квадратического отклонения по направлению главных осей рассеивания.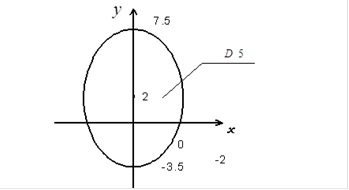
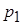 хотя бы одного попадания в область
хотя бы одного попадания в область 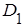 при трех независимых опытах перейдем к противоположному событию, т.е. к тому, что в результате трех опытов случайная точка ни разу не окажется в области
при трех независимых опытах перейдем к противоположному событию, т.е. к тому, что в результате трех опытов случайная точка ни разу не окажется в области 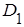 . Вероятность того, что случайная точка в результате опыта не попадет в область
. Вероятность того, что случайная точка в результате опыта не попадет в область 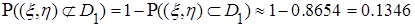
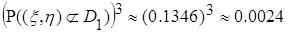
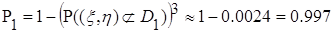
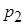 того, что при первых двух опытах случайная точка окажется хотя бы один раз в области
того, что при первых двух опытах случайная точка окажется хотя бы один раз в области 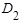 , равна по теореме умножения вероятностей произведению вероятности того, что при двух опытах случайная точка попадет хотя бы раз в область
, равна по теореме умножения вероятностей произведению вероятности того, что при двух опытах случайная точка попадет хотя бы раз в область 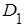 :
: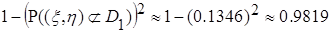
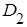 :
: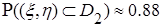 .
.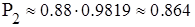 .
.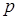 , то количество
, то количество 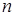 опытов, которые необходимо произвести для того, чтобы с вероятностью
опытов, которые необходимо произвести для того, чтобы с вероятностью 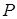 можно было утверждать, что данное событие произойдет хотя бы один раз, находится по формуле
можно было утверждать, что данное событие произойдет хотя бы один раз, находится по формуле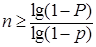 .
.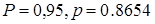 , тогда
, тогда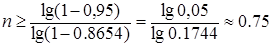 ,
,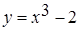 на отрезке [-2; 0] возможных значений случайной величины x монотонно возрастает и, следовательно, имеет обратную функцию
на отрезке [-2; 0] возможных значений случайной величины x монотонно возрастает и, следовательно, имеет обратную функцию  , которая монотонно возрастает на отрезке
, которая монотонно возрастает на отрезке 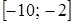 и является дифференцируемой. Поэтому искомую плотность вероятности найдем по формуле
и является дифференцируемой. Поэтому искомую плотность вероятности найдем по формуле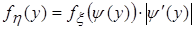 .
.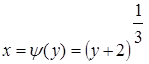 и учитывая, что
и учитывая, что ,
, 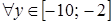 ,
,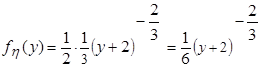 , если
, если 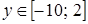 .
.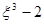 имеет следующую плотность вероятности:
имеет следующую плотность вероятности: =
= 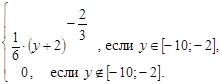
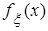 ,
, 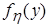 приведены на рис. 2.10, 2.11.
приведены на рис. 2.10, 2.11.

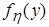 :
: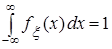 ,
, 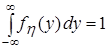
 ,
,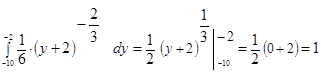
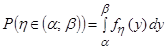 , находим искомую вероятность:
, находим искомую вероятность: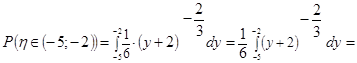
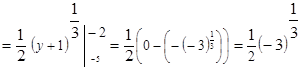
 , где
, где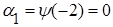 ,
, 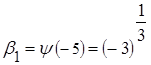 (здесь учтено, что функция
(здесь учтено, что функция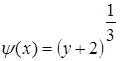 убывает на отрезке
убывает на отрезке 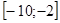 .
.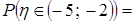
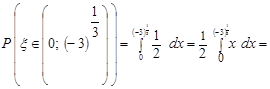
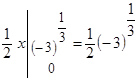 .
.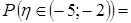
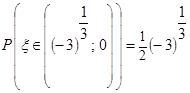 .
.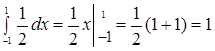 .
.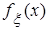 (рис. 2.12).
(рис. 2.12).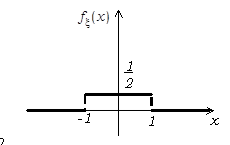
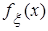 предлагается выполнить самостоятельно.
предлагается выполнить самостоятельно.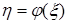 необязательно находить закон ее распределения; можно воспользоваться формулами
необязательно находить закон ее распределения; можно воспользоваться формулами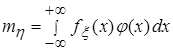 ,
,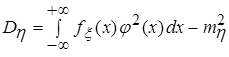 .
.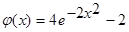 , получим:
, получим: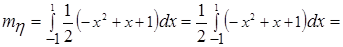
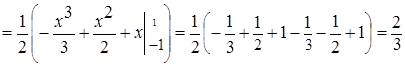 .
.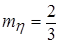 должен принадлежать интервалу возможных значений случайной величины h, т.е.
должен принадлежать интервалу возможных значений случайной величины h, т.е. 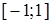 .
.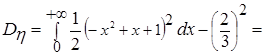

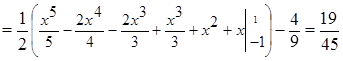 .
.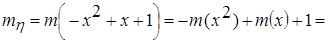

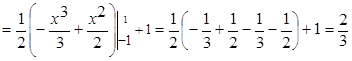 .
.
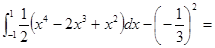
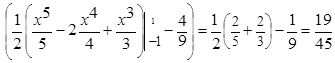 .
. .
.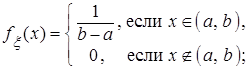
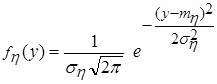
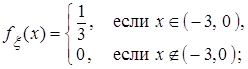
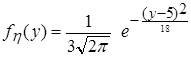
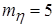 ,
, 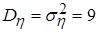 ,
, 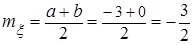 ,
,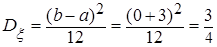
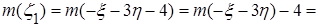
 ;
;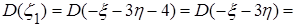
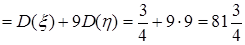
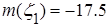 ,
, 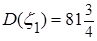 .
.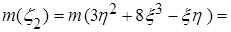
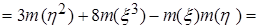
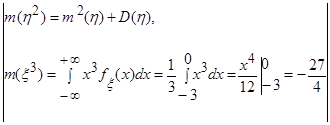 =
= 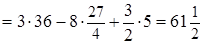 .
.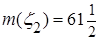 .
.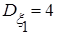 ,
, 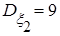 ,
, 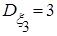 ;
;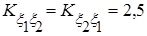 ,
, 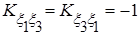 ,
, 
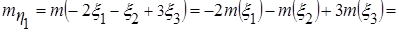
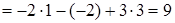 ;
;
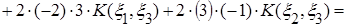
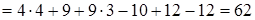 .
.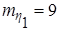 ,
, 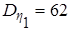 .
.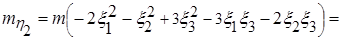
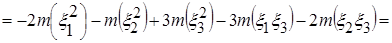
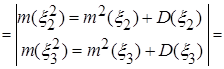
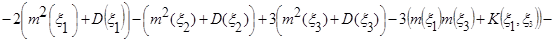
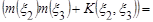
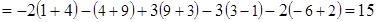 .
.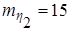
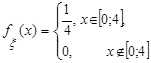 найти характеристическую функцию
найти характеристическую функцию  и с её помощью вычислить математическое ожидание
и с её помощью вычислить математическое ожидание  .
.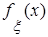 является оригиналом, то характеристическая функция
является оригиналом, то характеристическая функция 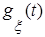 для неё является изображением. Найдём его, учитывая свойство линейности преобразования Лапласа и соотношение
для неё является изображением. Найдём его, учитывая свойство линейности преобразования Лапласа и соотношение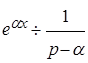 , где
, где 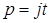

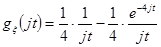
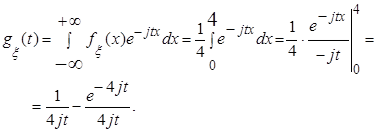
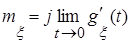 . Имеем:
. Имеем: