
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определенин усилий в стойках рамы.
Схема нагрузок на раму представлена на рис.18. Так как жесткость фермы значительно больше жесткости колонны (стойки), ригель рамы представляем как абсолютно жесткое тело. Упрощённая расчётная схема представлена на рис.17. Ригель крепится к стойкам шарнирно, а сами стойки жестко защемлены в основании. В этом случае рама один раз статически неопределима.
Разрежем ригель и рассмотрим условие совместности деформаций. Так как ригель жесткий, перемешение верхних концов стоек будет одинаковым (см. Рис.18). Обозначим горизонтальное усилие, приложенное к шарниру левой стойки как Х. Тогда усилие на правой стойке будет определяться как FWO-X. (см. Рис.19). Такая схема реализуется при отсутствии или разрушении торцовых стен.
Рис.18. Рис.19.
Суммарное горизонтальное перемещение конца левой стойки равно суммарному горизонтальному перемещению конца правой стойки, или
X×H3/3EI + qW ×H4/8EI = (FWO –X)×H3/3EI + q После сокращения на EI и Н3 и преобразований, получим:
X/3 – (FWO-X)/3 = 2X = 3 X=[FWO -3(qW - q Опорные моменты в стойках Mлев = X×H + 0,5×qw×H2 = 3,32×10 + 0,5×1,545×102 = 110,5 кН×м Mправ = (Fwo –X)H + 0,5
Рис.20. Рис.21.
Эпюры изгибающих моментов представлены на Рис.20. Наибольший изгибающий момент - момент в опоре левой стойки.
Однако, в реальных конструкциях всегда присутствуют торцовые стены, и, поэтому, шарниры на верхних концах стоек не могут перемещаться. Расчётная схема стойки в этом случае представлена на Рис.21. Здесь же дана эпюра изгибающих моментов (по справочникам) для левой стойки, как наиболее нагруженной.
Момент на опоре: Моп =qW ∙Н2 /8 = 1,545∙102/8 = 19,3 кН∙м Максимальный изгибающий момент в пролёте: Мпр =qW ∙Н2 /12,8 = 1,545∙102/12,8 = 12,1 кН∙м
Расчёт и конструирование колонны
Расчёт стержня колонны.
Колонны промышленных зданий работают на внецентренное сжатие. Значения расчётных усилий (продольной силы N, изгибающего момента в плоскости рамы Mx и поперечной силы Q), определены по результатам статического расчёта рамы (см. п.6 выше). Расчётная длина в плоскости рамы определяется с учётом ряда упрощающих предпосылок:
- колонна рассматривается как отдельно стоящий стержень с идеализированными условиями закрепления; - система загружается силами, приложенными только в узлах; - пространственная работа каркаса учитывается не в полной мере. Такой подход идёт в запас устойчивости.
Для колонны с постоянным по высоте сечением коэффициент расчётной длины m принимают в зависимости от способа закрепления колонны в фундаменте и соотношения погонных жесткостей ригеля и колонны. (см. СНиП II-23-85, п.6, табл.17а)
При жестком закреплении колонн в фундаменте (как в настоящем примере) m = При шарнирном закреплении ригеля к колонне n=0, тогда m= Сплошные колонны обычно проектируют двутаврового сечения. Для колонн с постоянным по высоте сечением применяются симметричные двутавры. Для снижения трудоёмкости изготовления колонн рационально применение прокатных профилей с параллельными гранями, типа Ш.
Последовательность подбора сечения сплошных колонн. Расчёт производим для левой стойки рамы (колонны), у которой изгибающий момент от горизонтальной нагрузки имеет наибольшую величину. 1. Находим коэффициент приведения m (он определён выше, m=2,0 2. Определяем расчётные длины lx и ly: lx = ly = m× l =2×10 =20 м =2000 см, где l =H=10 м – высота колонны; 3. Задаёмся высотой сечения колонны. При высоте Н до 12 м, h=Н/15 =1000/15=66,7 см. По сортаменту ГОСТ 26020-83, предварительно выбираем широкополочный двутавр 70Ш1, геометрические характеристики которого: h=683 мм – высота сечения; А=216,4 см2 – площадь сечения; Ix= 172000 см4 - момент инерции площади поперечного сечения относительно оси x; Wx= 5036 см3 – момент сопротивления площади сечения относительно оси x; ix =28,19 см – радиус инерции относительно оси x; Iy = 10400 см4 - момент инерции площади поперечного сечения относительно оси y; iy =6,93 см – радиус инерции относительно оси y; b=320 мм – ширина полки; s=13,5 мм – толщина стенки; t=19,0 мм –толщина полки.
4. Определяем условную гибкость
mx = eA/Wx где e – эксцентриситет, определяемый выражением e=Mmax/N e=110,5/266=0,415 м=41,5 см; mx= 41,5×216,4/5036 =1,78 здесь: Mmax=110,5 кН×м – максимальный изгибающий момент в колонне;
N = 266 кН – центрально приложенная сжимающая продольная сила, равная опорной реакции фермы. 5. По полученным значениям mx и Предварительно опредеяем соотношение Af /Aw =608/926 = 0,66 где: Af = b∙t = 32∙19,0 = 608 см2 - площадь полок двутавра; Aw = h∙s =68,3∙13,5 = 926 см2;
При mx = 1,78 и при Af /Aw =0,66 и
h = (1,75-0,1mx) – 0,02(5-mx) Приведенный относительный эксцентриситет mef=h×mx = ×094•1,78=1,67 при
при при при
Требуемая площадь сечения
Атр = N / (φe·Ry γc) = 266/(0,435×34,5×0,95) =18,7 см2 ˂ 216,4 см2, поэтому можно назначить двутавр меньшего размера. Назначаем двутавр 40Ш1, для которого:
h=388 мм – высота сечения; А=122,4 см2 – площадь сечения; Ix= 34360 см4 - момент инерции площади поперечного сечения относительно оси x; Wx= 1771 см3 – момент сопротивления площади сечения относительно оси x; ix =16,76 см – радиус инерции относительно оси x; Iy = 6306 см4 - момент инерции площади поперечного сечения относительно оси y; iy =7,18 см – радиус инерции относительно оси y;
Далее проводим повторный расчёт
Определяем условную гибкость
mx = eA/Wx где e – эксцентриситет, определяемый выражением e=Mmax/N e=110,5/266=0,415 м=41,5 см; mx= 41,5×122,4/1771 =2,9 По полученным значениям mx и При mx = 2,9 и при Af /Aw =0,5 и h = (1,75-0,1mx) – 0,02(5-mx) Приведенный относительный эксцентриситет mef=h×mx = 1,25×2,9=3,6 при
при при при
Требуемая площадь сечения Атр = N / (φe·Ry γc) = 266/(0,160×34,5×0,95) =50,7 см2 ˂ 122,4 см2. Так как требуемая площадь практически в 2 раза меньше чем у принятого двутавра, берём двутавр 35Ш1, для которого:
h=338 мм – высота сечения; А=95,67 см2 – площадь сечения; Ix= 19790 см4 - момент инерции площади поперечного сечения относительно оси x; Wx= 1171 см3 – момент сопротивления площади сечения относительно оси x; ix =14,38 см – радиус инерции относительно оси x; Iy = 3260 см4 - момент инерции площади поперечного сечения относительно оси y; iy =5,84 см – радиус инерции относительно оси y; bf=250 мм – ширина полки; s=9,5 мм – толщина стенки; tf=12,5 мм –толщина полки.
Далее проводим повторный расчёт
Определяем условную гибкость
mx = eA/Wx где e – эксцентриситет, определяемый выражением e=Mmax/N e=110,5/266=0,415 м=41,5 см; mx= 41,5×95,6/1171 =3,4 По полученным значениям mx и При mx = 3,4 и при Af /Aw =0,5 и h = 1,25 Приведенный относительный эксцентриситет mef=h×mx = 1,25×3,4=4,25 при
при при при
Требуемая площадь сечения Атр = N / (φe·Ry γc) = 266/(0,124×34,5×0,95) =65,5 см2 ˂ 95,67 см2.
6. Проверяем устойчивость колонны из плоскости изгиба
Требуемая площадь сечения Атр = N / (φ·Ry γc) = 266/(0,158×34,5×0,95) =51,4 см2 ˂95,67 см2 у принятого двутавра. где j = 0,158 (получено интерполяцией значений по табл.72, СНиП II-23-85), при l = ly / iy = 1000/5,84 =170 Устойчивость колонны из плоскости изгиба обеспечена.
|
|||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 1084; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.20.205.228 (0.033 с.) |


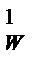 ×H4/8EI
×H4/8EI или (2X-FWO)/3 =
или (2X-FWO)/3 =  )H/8]/2 = [8,09 – 3(1,545 – 1,16)10/8]/2 = 3,32 кН
)H/8]/2 = [8,09 – 3(1,545 – 1,16)10/8]/2 = 3,32 кН ×H2 = (8,09- 3,32)×10 + 0,5×1,16×102 = 105,7 кН
×H2 = (8,09- 3,32)×10 + 0,5×1,16×102 = 105,7 кН
 ;
; =2,0
=2,0 x и относительный эксцентриситет mx
x и относительный эксцентриситет mx = (2000/28,19)
= (2000/28,19) 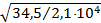 =2,9
=2,9 x =4,05 и mef = 1,67 je определяем интерполяцией:
x =4,05 и mef = 1,67 je определяем интерполяцией:


