
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Принципы построения общих индексов
Общие индексы используются для сопоставления непосредственно несоизмеримых, разнородных явлений. Однако нельзя просто сложить объемы продукции различных видов за два периода и отнести эти суммы одну к другой, потому что различные виды продукции неравноценны по количеству затраченного на них общественного труда и имеют разные потребительские стоимости. Чтобы преодолеть несуммарность отдельных элементов изучаемого явления в индекс вводится дополнительный неизменный показатель (соизмеритель). При построении индексов объемных показателей (выпуска объема продукции, физического объема реализации товаров, среднесписочной численности работников и т.д.) в качестве соизмерителей применяются те или иные качественные показатели. Качественные интенсивные показатели характеризуют размер признака в расчете на единицу совокупности: цена единицы продукции (товара), себестоимость единицы продукции, выработка продукции на одного работающего и т.д. При построении индексов качественных показателей (цен, себестоимости, производительности труда, средней заработной платы и т.д.) в качестве соизмерителя применяются те или иные объемные показатели (экстенсивные). Соответствующие количественные (объемные) и качественные показатели должны быть тесно связаны друг с другом и путем перемножения образовать новый показатель, другую экономическую категорию(стоимость выпущенной продукции, стоимость реализованных товаров, фонд зарплаты и т.д.). В числителе и знаменателе индексного отношения будут суммы произведений индексируемых величин на их веса. Это и есть агрегатные индексы. Индексируемой величиной называется показатель (признак), изменение которого выявляют. Весом называется показатель, который выступает в качестве соизмерителя. Существует правило построения агрегатных факторных индексов, в соответствии с которым в индексах качественных показателей весами выступают показатели отчетного периода, а в индексах количественных показателей - базисного периода. Так, агрегатный индекс цен (
где
Этот индекс характеризует, как изменились в среднем цены на различные виды продукции (товаров), включенные в расчет общего индекса цен. Агрегатный индекс физического объема (
где Индекс физического объема характеризует, как изменился в среднем общий объем продукции по анализируемому перечню. Индекс стоимости продукции товарооборота (
Длимый индекс характеризует изменение фактической стоимости произведенной или реализованной продукции или же размера товарооборота по анализируемому перечню. Произведение агрегатного индекса на агрегатный индекс физического объема равно агрегатному индексу стоимости продукции (товарооборота):
Используя эту взаимосвязь, можно по двум известным индексам определить третий. Общие индексы дают возможность определить не только относительные изменения явления, но и найти абсолютные значения изменений как разницу между числителем и знаменателем соответствующих индексов. Абсолютное изменение общей стоимости продукции (товаров) исчисляется по формуле:
в том числе за счет следующих факторов: · изменения уровней цен: · изменения физического объема продукции (товаров):
где
При этом должно соблюдаться равенство:
Аналогично агрегатным индексам цен физического объема и стоимости продукции (товарооборота) строятся и рассчитываются агрегатные индексы других взаимосвязанных экономических показателей.
Средние индексы Агрегатный индекс является основной формой общего индекса. Средние из индивидуальных индексов выступают как преобразованная форма агрегатного индекса и дают результаты тождественные этим индексам. При исчислении средних индексов могут быть использованы две формы средних: средняя арифметическая и средняя гармоническая.
Выбор формы индекса зависит от характера исходных данных, если известны абсолютные значения индексируемого показателя и веса в отчетном и базисном периодах, то пользуются агрегатной формой индексов. Если известны относительные изменения индексируемых показателей по отдельным единицам изучаемой совокупности, то пользуются формой средних индексов (арифметической или гармонической). Так, для получения среднего арифметического индекса физического объема продукции (или товарооборота) необходимо в числителе агрегатного индекса
Этот индекс представляет собой среднюю арифметическую индивидуальных индексов физического объема ( Результат совпадает с полученным раньше при использовании агрегатной формы индекса физического объема. Рассмотрим преобразование агрегатного индекса в средний гармоний на примере индекса цен. В знаменателе агрегатного индекса цен Числитель индекса оставим без изменения. Тогда формула индекса примет следующий вид:
Этот индекс представляет среднюю гармоническую индивидуальных индексов (
Цепные и базисные индексы Для изучения динамики показателя за ряд последовательных периодов рассчитывается система цепных и базисных индексов. Базисные индексы характеризуют относительное изменение уровня изучаемого явления в какой-то определенный период по сравнению с периодом, принятым за базу сравнения. Цепные индексы характеризуют относительное изменение уровня изучаемого явления по сравнению с предшествующим периодом. Система цепных и базисных индексов может быть исчислена как для отдельного элемента сложного явления (индивидуальные индексы), так и для всего сложного явления (общие индексы). Для индивидуальных индексов объемных и качественных показателей справедливы следующие правила: 1. Произведение цепных индексов за определенный период дает базисный индекс за этот же период. 2. Отношение базисного индекса отчетного периода к базисному индексу предшествующего периода дает цепной индекс отчетного периода. При построении системы общих агрегатных цепных и базисных индексов одного и того же явления возникает вопрос о выборе весов (соизмерителей). В каждом отдельном общем индексе веса остаются отменными, изменяется только индексируемая величина. Но если строить систему цепных или базисных индексов, то веса в них могут быть либо одинаковые (постоянные) для всех индексов, либо меняться от одного индекса к другому. Когда веса какого-либо одного периода (первоначального или базисного) постоянные для всех индексов, последние называются индексами с постоянными весами. Эти индексы, как правило, строятся для количественных (объемных) показателей, что соответствует принципам построения агрегатных индексов. Если веса изменяются при переходе от одного индекса к другому, то это индексы с переменными весами. Переменные веса – это, как правило, веса отчетного (текущего) периода. С такими весами обычно строятся ряды агрегатных индексов качественных показателей: цены, себестоимости, трудоемкости и т.д.
Возьмем ряд анализируемых величин за период: · себестоимость единицы продукции: · количество единиц продукции: Построим системы агрегатных цепных и базисных индексов с переменными и постоянными весами. Общие индексы себестоимости с переменными весами рассчитываются следующим образом: · цепные по следующим формулам:
· базисные по следующим формулам:
Общие индексы физического объема продукции с постоянными весами исчисляются следующим образом: · цепные по следующим формулам:
· базисные по следующим формулам:
Индексы с постоянными весами в отличие от индексов с переменными позволяют исключить влияние изменения структуры на динамику индексируемой величины. Индексы с постоянными весами можно сравнивать между собой. Для них справедлива взаимосвязь, отмеченная выше для индивидуальных индексов. У индексов с переменными весами такая взаимосвязь отсутствует. Аналогично приведенным выше индексам себестоимости и физического объема строятся ряды цепных и базисных индексов с переменными и постоянными весами для других взаимосвязанных экономических показателей.
|
|||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 1230; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.115.195 (0.025 с.) |
 )определяется по формуле:
)определяется по формуле:
 - цена каждого вида продукции (товара) соответственно в базисном и отчетном периодах (индексируемый показатель);
- цена каждого вида продукции (товара) соответственно в базисном и отчетном периодах (индексируемый показатель); - объем каждого вида продукции (товара) в отчетном периоде (все индекса).
- объем каждого вида продукции (товара) в отчетном периоде (все индекса). ) рассчитывается по следующей формуле:
) рассчитывается по следующей формуле:
 объем каждого вида продукции (товара) в базисном периоде.
объем каждого вида продукции (товара) в базисном периоде. ) определяется следующим образом:
) определяется следующим образом:




 и
и  - стоимость произведенной или реализованной продукции (товарооборота) соответственно в базисном и отчетном периодах;
- стоимость произведенной или реализованной продукции (товарооборота) соответственно в базисном и отчетном периодах;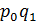 - стоимость продукции (товарооборот) в сопоставимых ценах.
- стоимость продукции (товарооборот) в сопоставимых ценах.
 заменить
заменить  (так как iq =
(так как iq =  , откуда
, откуда  Знаменатель индекса оставим без изменения. В результате получим следующую формулу:
Знаменатель индекса оставим без изменения. В результате получим следующую формулу:
 ), взвешенных по стоимости продукции (товарооборота) базисного периода (
), взвешенных по стоимости продукции (товарооборота) базисного периода ( ).
). заменим
заменим  на отношение
на отношение  (так как
(так как 
 ).
). /
/ ), взвешенных по стоимости продукции (товарообороту) отчетного периода (
), взвешенных по стоимости продукции (товарообороту) отчетного периода (
 .
. =
=  ,
,  =
= 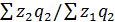 , …
, …  =
=  ,
, , …
, …  .
. =
=  ,
,  =
= 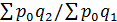 , …
, …  =
=  ,
, , …
, …  .
.


