
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ошибки выборочного наблюдения
При проведении выборочного наблюдения допускаются ошибки двух видов: ошибки регистрации и ошибки репрезентативности. Ошибки регистрации могут быть при проведении всех видов наблюдения. Они зависят от добросовестности и квалификации регистраторов, правильности ответов опрашиваемых и т.д. Ошибки репрезентативности свойственны только выборочным наблюдениям. И те и другие ошибки могут быть случайными и систематическими. Случайные ошибки – несущественные, так как отклонения в сторону уменьшения или увеличения встречаются одинаково часто, и взаимно погашаются. Систематические ошибки существенно искажают результаты, так как допускаются отклонения в одну сторону, эти ошибки являются следствием нарушения принципа случайного отбора. При соблюдении принципа случайного отбора ошибка выборки определяется прежде всего численностью выборки. Чем больше численность выборки при прочих равных условиях, тем меньше величина ошибки выборки. Ошибка выборки также определяется степенью варьирования изучаемого признака, а степень варьирования характеризуется в статистике средним квадратом отклонений – дисперсией. Средняя ошибка выборки (μ) при собственно-случайном повторном отборе определяется следующим образом: · Для среднего значения признака по формуле · Для доли альтернативного признака по формуле Применительно к бесповторной выборке в формулы средней ошибки выборки необходимо добавить дополнительный множитель в подкоренное выражение (1 – (n / N)), тогда формулы средней ошибки выборки примут следующий вид: · Для среднего значения признака: · Для доли альтернативного признака: численность генеральной совокупности. Предельную ошибку выборки (
где t – коэффициент доверия, величина которого зависит от заданной вероятности (p) и определяется по специальным таблицам, исчисленным по интегралу Лапласа. Эти таблицы обычно приводятся в учебниках и учебных пособиях по статистике. Например, при p=0,683, t=1; при p=0,954, t=2; при p=0,997, t=3. Если в вышеприведенную формулу предельной ошибки выборки подставить значение средней ошибки выборки, то формула предельной ошибки выборки для среднего значения признака примет следующий вид:
· при повторном отборе: · при бесповторном отборе:
Предельная ошибка выборки для доли альтернативного признака определяется следующим образом: · при повторном отборе по формуле · при бесповторном отборе по формуле Границы (пределы) доли признака по всей (генеральной) совокупности определяются следующим неравенством:
где p – доля альтернативного признака по генеральной совокупности.
Определение численности выбора Приведенные формулы для определения величины ошибки выборки дают возможность не только определять эти ошибки, но и рассчитывать предварительно, какую необходимо взять численность выборки, чтобы ошибка выборки не превышала определенные заданные размеры. Путем несложного преобразования формул предельной ошибки выборки можно получить формулы для определения необходимой численности выборки при повторном отборе: · для среднего значения признака: тогда · для доли альтернативного признака:
Необходимая численность выборки при бесповторном отборе рассчитывается по следующим формулам: · для среднего значения признака: · для доли альтернативного признака:
При использовании этих формул для расчета достаточной для исследования численности выборки возникают трудности с определением дисперсии. Поэтому часто вместо фактического значения дисперсии в формулы подставляют ее приближенные значения, полученные в предыдущих аналогичных выборочных наблюдениях. Для альтернативных признаков обычно используют ее максимальное значение (0,25).
Тема 7. СТАТИСТИЧЕСКОЕ ИЗУЧЕНИЕ СОЦИАЛЬНО-ЭКОНОМИЧЕСКИХ ЯВЛЕНИЙ Ряды динамики и их виды
|
|||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 458; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.19.30.232 (0.008 с.) |
 ;
; , где n – численность выборочной совокупности;
, где n – численность выборочной совокупности;  - дисперсия признака;
- дисперсия признака;  - доля единиц совокупности с заданным значением признака в общей их численности по выборке.
- доля единиц совокупности с заданным значением признака в общей их численности по выборке. ;
; , где N –
, где N – ) находят по формуле
) находят по формуле ,
, ;
; .
. ;
; .
.
 то:
то: 
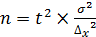 ,
, то:
то: тогда
тогда  .
.




