
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Условные законы распределения составляющих системы непрерывных случайных величин.
Пусть (ξ, η) - непрерывная двумерная случайная величина. Определение. Условной плотностью φ (х | y) распределения составляющих ξ при данном значении η=y называют отношение плотности совместного распределения f (х, у) системы (ξ, η) к плотности распределения f2 (y) составляющей η: φ (х | y)= f (х, у)/ f2 (y). Отличие условной плотности φ (х | y) от безусловной плотности f1 (x) состоит в том, что функция φ (х | y) дает распределение ξ при условии, что составляющая η приняла значение η=y; функция же f1 (x) дает распределение ξ независимо от того, какие из возможных значений приняла составляющая η. Аналогично определяется условная плотность составляющей η при данном значении ξ = х: ψ (y | x) =f (x, y)/ f1 (x). Если известна плотность совместного распределения f (x, у), то условные плотности составляющих могут быть найдены по формулам: φ (х | y)= f (х, у)/ ψ (y | x) =f (x, y)/ Запишем представленные соотношения в виде: f (х, у)= f2 (y) φ (х | y), f (х, у)= f1 (x) ψ (х | y). Отсюда заключаем: умножая закон распределения одной из составляющих на условный закон распределения другой составляющей, найдем закон распределения системы случайных величин. Как и любая плотность распределения, условные плотности обладают следующими свойствами: φ (х | y)≥ 0, ψ(y|x)≥0, Пример. Двумерная случайная величина (ξ, η) задана плотностью совместного распределения f (x, у)= Найти условные законы распределения вероятностей составляющих. Решение. Найдем условную плотность составляющей ξ при | x |< φ (х | y)= Так как f (x, у)= 0 при х2 + y2 > r2, то φ (х | y) =0 при | x |> Аналогично найдем условную плотность составляющей ψ (y | x)=
§21. Зависимые и независимые случайные величины
Определение. Две случайные величины называются независимыми, если закон распределения одной из них не зависит от того, какие возможные значения приняла другая величина. Из этого определения следует, что условные распределения независимых величин равны их безусловным распределениям. Выведем необходимые и достаточные условия независимости случайных величин. Теорема. Для того чтобы случайные величины ξ и η были независимыми, необходимо и достаточно, чтобы функция распределения системы (ξ, η) была равна произведению функций распределения составляющих:
F (x, y)= F1 (x) F2 (y). Доказательство. а) Необходимость. Пусть ξ и η независимы. Тогда события ξ < х и η < у независимы, следовательно, вероятность совмещения этих событий равна произведению их вероятностей: Р (ξ < х, η < у)= Р (ξ < х) P (η < у), или F (x, y)= F1 (x) F2 (y). б) Достаточность. Пусть F (x, y)= F1 (x) F2 (y). Отсюда Р (ξ < х, η < у)= Р (ξ < х) P (η < у), т.е. вероятность совмещения событий ξ < х и η < у равна произведению вероятностей этих событий. Следовательно, случайные величины ξ и η независимы. Следствие. Для того чтобы непрерывные случайные величины ξ и η были независимыми, необходимо и достаточно, чтобы плотность совместного распределения системы (ξ, η) была равна произведению плотностей распределения составляющих: f (x, y)= f1 (x) f2 (y). Доказательство. а) Необходимость. Пусть ξ и η - независимые непрерывные случайные величины. Тогда (на основании предыдущей теоремы) F (x, y)= F1 (x) F2 (y). Дифференцируя это равенство по х, затем по у, имеем
или (по определению плотностей распределения двумерной и одномерной величин) f (x, y)= f1 (x) f2 (y). б) Достаточность. Пусть f (x, y)= f1 (x) f2 (y). Интегрируя это равенство по х и по у, получим
или F (x, y)= F1 (x) F2 (y). Отсюда (на основании предыдущей теоремы) заключаем, что ξ и η независимы.
§22. Математическое ожидание дискретной случайной величины
Закон распределения полностью характеризует случайную величину. Однако часто закон распределения неизвестен и приходится ограничиваться меньшими сведениями. Иногда даже выгоднее пользоваться числами, которые описывают случайную величину суммарно; такие числа называют числовыми характеристиками случайной величины. К числу важных числовых характеристик относится математическое ожидание. Определение. Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности. Пусть случайная величина ξ может принимать только значения x1, x2,..., xп, вероятности которых соответственно равны р 1, р 2,..., рп. Тогда математическое ожидание М (ξ) случайной величины ξ определяется равенством
М (ξ)= x1р1 + x2р2 +...+ x прп. Если дискретная случайная величина ξ принимает счетное множество возможных значений, то М (ξ)= причем математическое ожидание существует, если ряд в правой части равенства сходится абсолютно. Из определения следует, что математическое ожидание случайной величины есть неслучайная (постоянная) величина. Пример. Найти математическое ожидание случайной величины ξ, зная закон ее распределения:
Решение. Искомое математическое ожидание равно сумме произведений всех возможных значений случайной величины на их вероятности: М(ξ)=3·0,1+5·0,6+2·0,3=3,9. Пример. Найти математическое ожидание числа появлений события А в одном испытании, если вероятность события А равна р. Решение. Случайная величина ξ - число появлений события А в одном испытании -может принимать только два значения: x1=1 (событие А наступило) с вероятностью р и x2=0 (событие А не наступило) с вероятностью q=1-р. Искомое математическое ожидание М(ξ)=1·р+0·q=p. Итак, математическое ожидание числа появлений события в одном испытании равно вероятности этого события.
|
||||||||||||||
|
Последнее изменение этой страницы: 2017-02-21; просмотров: 309; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.171.20 (0.012 с.) |
 dx,
dx, dx=1;
dx=1;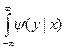 dy=1.
dy=1.
 :
: =
=  .
.
 =
= 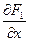
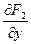 ,
, dx dy =
dx dy =  dx
dx  dy,
dy, ,
,


