
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойства двумерной плотности вероятности.
Свойство 1. Двумерная плотность вероятности неотрицательна: f (x, y)≥ 0. Доказательство. Вероятность попадания случайной точки в прямоугольник со сторонами ∆ х и ∆ у есть неотрицательное число; площадь этого прямоугольника - положительное число. Следовательно, отношение этих двух чисел, а значит, и их предел (при ∆ x → 0 и ∆ y → 0), который равен f (x, y), есть неотрицательное число, т.е. f (x, y)≥ 0. Свойство непосредственно следует из того, что F (x, у) - неубывающая функция своих аргументов. Свойство 2. Двойной несобственный интеграл с бесконечными пределами от двумерной плотности равен единице:
Доказательство. Бесконечные пределы интегрирования указывают, что областью интегрирования служит вся плоскость х0у; поскольку событие, состоящее в том, что случайная точка попадет при испытании на плоскость х0у, достоверно, то вероятность этого события (она и определяется двойным несобственным интегралом от двумерной плотности) равна единице, т. е.
Пример. Задана плотность совместного распределения непрерывной двумерной случайной величины (ξ, η): f (х, у)= С cos x cos у в квадрате (0≤х≤π/2, 0≤у≤π/2; вне этого квадрата f (х, у) =0). Найти постоянный параметр С. Решение. Воспользуемся свойством 2, учитывая, что х и у изменяются от 0 до π/2: C Отсюда С = Выполнив интегрирование, получим искомое значение параметра С = 1.
Отыскание плотностей вероятности составляющих двумерной случайной величины.
Пусть известна плотность совместного распределения вероятностей системы двух случайных величин. Найдем плотности распределения каждой из составляющих. Найдем сначала плотность распределения составляющей ξ. Обозначим через F1 (x) функцию распределения составляющей ξ. По определению плотности распределения одномерной случайной величины, f1 (х)= Приняв во внимание соотношения F (x, у)= F1 (x)= F (x,∞), найдем F1 (x)= Продифференцировав обе части этого равенства по х, получим
или f1 (х)= Аналогично находится плотность распределения составляющей η: f2 (у)=
Итак, плотность распределения одной из составляющих равна несобственному интегралу с бесконечными пределами от плотности совместного распределения системы, причем переменная интегрирования соответствует другой составляющей.
Пример. Двумерная случайная величина (ξ, η) задана плотностью совместного распределения f (x, у)= Найти плотности распределения составляющих ξ и η. Решение. Найдем плотность распределения составляющей ξ f1 (х)= Итак, f1 (x)= Аналогично найдем плотность распределения составляющей η: f2 (у)= Найденные функции удовлетворяют соотношениям
§20. Условные распределения
|
|||||
|
Последнее изменение этой страницы: 2017-02-21; просмотров: 654; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.14.70.203 (0.007 с.) |
 dx dy=1.
dx dy=1. dx dy=1.
dx dy=1. .
. .
.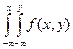 dx dy,
dx dy, dx dy.
dx dy. dу,
dу,

 =
= 
 =
= 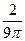
 .
.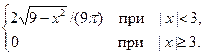

 dх = 1 и
dх = 1 и  dу = 1.
dу = 1.


