
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Проверка однородности выборочных средних
Данная процедура позволяет установить, вызвано ли расхождение между средними случайными ошибками измерений или оно связано с влиянием каких либо случайных факторов. Эта процедура используется, например, при установлении идентичности параметров деталей, изготовленных на разном оборудовании. Проверка гипотезы об однородности средних осуществляется по критерию Стьюдента. · Если
Если Формула становится проще, если
· В том случае, если дисперсии
Число степеней свободы
Проверка гипотезы о нормальном законе распределения 1. Проверка гипотезы о нормальном законе распределения по критерию Пирсона
Для проверки данной гипотезы весь интервал возможных значений случайной величины разбивается на Вычисляются теоретические вероятности
Здесь Для проверки гипотезы о законе нормального распределения используется табулированная нормированная функция Лапласа. Нормированная функция Лапласа определяется как интеграл вида:
Расчетный коэффициент Пирсона
Здесь Гипотеза о нормальном законе распределения случайной величины принимается в том случае, если 2. Проверка гипотезы о нормальном законе распределения по критерию Колмогорова. Проверка нормального распределения по критерию Колмогорова основана на использовании показателей асимметрии и эксцесса. Коэффициент асимметрии
где
Затем вычисляются среднеквадратические отклонения для коэффициента асимметрии
Если приведенные ниже неравенства выполняются, то можно принять гипотезу о нормальном законе распределения
1.22. Другие наиболее известные виды законов распределения [14] Биномиальное распределение Если в серии независимых опытов, каждый из которых заканчивается появлением или не появлением некоторого события А, тогда можно считать, что событие А происходит с вероятностью Р(А), тогда непоявления события А будет равна q(А) = 1
Уравнение (1.81) описывает биномиальное распределение случайного числа k. Здесь
Из вышеизложенного следует, что формула (1.81) будет иметь вид
Математическое ожидание
и дисперсия
Пример. На некотором участке цеха в час обрабатываются 100 деталей, 2 из которых могут быть бракованными. Какова вероятность того, что из 100 деталей две могут быть бракованными? Здесь
Распределение Пуассона
считать, что событие А раз произойдет в
Уравнение (1.86) представляет собой распределение Пуассона. Если число опытов
Поскольку
(1.86)
Пример. Пусть в некоторой партии готовых деталей есть порядка 1% бракованных деталей. Определить вероятность того, что в выбранной партии из 50 деталей, находятся 0, 1, 2, или 3 бракованные
Распределение Пуассона обычно применяется в производстве для выборочного контроля качества готовой продукции, когда допускается небольшой процент брака, то есть при
Робастность Принадлежность случайной величины к тому или иному теоретическому распределению (закону распределения) накладывает некоторые существенные ограничения, которые на практике не всегда выполняются. Поэтому особенно ценными оказываются методы, которые можно применять в широком диапазоне изменения условий. Незначительная (небольшая) чувствительность к отклонениям от теоретических условий называется робастностью. Применяемые на практике методы в реальных условиях называются робастными [28]. Робастность связана с определенными отклонениями от теоретических условий. Она может относиться к неоднородности дисперсий, к отсутствию независимости опытов, невыполнению условия принадлежности к нормальному распределению и т. д.
1.24. Коэффициент корреляции [24, 26] Коэффициент корреляции
а) б)
Рисунок 1.19. Статистические зависимости а) прямо пропорциональная ( б) обратно пропорциональная (
Выборочный коэффициент корреляции находится в пределах
Анализ этой формулы показывает, что чем дисперсии больше, тем зависимость менее определенная, то есть коэффициент корреляции меньше. Более ярко выраженная зависимость делает коэффициент корреляции ближе к единице по абсолютной величине, рисунок 1.20.
Рисунок 1.20. Коэффициент корреляции
Формула для вычисления выборочного коэффициента корреляции имеет вид:
Здесь Для того, чтобы убедиться в том, что статистическую зависимость можно считать значимой с выбранным уровнем значимости
Число степеней свободы берется равным Используя соответствующую статистическую таблицу выбираем Если Значимость коэффициента корреляции можно проверить с помощью графика, показанного на рисунке 1.21.
Рисунок 1.21. График для проверки значимости коэффициента корреляции
На рисунке 1.21 кривыми линиями плоскость разделена на три зоны: · I – коэффициент корреляции незначим; · II - коэффициент корреляции значим;
Истинный коэффициент корреляции определяется как предел абсолютной величины выборочного коэффициента корреляции
(1.90)
|
||||||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 238; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.208.117 (0.038 с.) |
 и
и 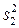 однородны, то
однородны, то  вычисляется по формуле:
вычисляется по формуле: (1.70)
(1.70) гипотеза об однородности средних принимается. Число степеней свободы для выбора
гипотеза об однородности средних принимается. Число степеней свободы для выбора 

 Тогда
Тогда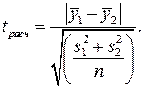 (1.71)
(1.71) (1.72)
(1.72) вычисляется по формуле:
вычисляется по формуле: (1.73)
(1.73)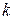 подинтервалов. В каждый подинтервал попадает по
подинтервалов. В каждый подинтервал попадает по  значений случайной величины
значений случайной величины 


 нижняя и верхняя границы
нижняя и верхняя границы 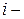 го подинтервала соответственно,
го подинтервала соответственно,  выборочное среднее,
выборочное среднее,  среднеквадратическое отклонение.
среднеквадратическое отклонение. (1.74)
(1.74) определяется по формуле:
определяется по формуле: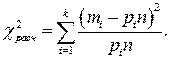 (1.75)
(1.75)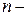 объем выборки, число степеней свободы
объем выборки, число степеней свободы  Одна степень свободы падает на выборочное среднее, вторая на выборочную дисперсию, третья на выбор закона распределения.
Одна степень свободы падает на выборочное среднее, вторая на выборочную дисперсию, третья на выбор закона распределения. Здесь
Здесь 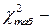 табличное значение коэффициента Пирсона.
табличное значение коэффициента Пирсона. и коэффициент эксцесса
и коэффициент эксцесса  рассчитываются по формулам:
рассчитываются по формулам: (1.76)
(1.76) и эксцесса
и эксцесса  по формулам:
по формулам: (1.77)
(1.77)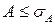 и
и  (1.78)
(1.78) Р(А). Все результаты опытов независимы друг от друга, поэтому наступление события А (или не наступление события А) не зависит от результатов предыдущих опытов. В этом случае вероятность наступления события А определенное число раз происходит по закону биномиального распределения. Если вероятность появления события А постоянна и равна Р(А), то вероятность наступления события А точно k раз в n испытаниях будет определяться уравнением
Р(А). Все результаты опытов независимы друг от друга, поэтому наступление события А (или не наступление события А) не зависит от результатов предыдущих опытов. В этом случае вероятность наступления события А определенное число раз происходит по закону биномиального распределения. Если вероятность появления события А постоянна и равна Р(А), то вероятность наступления события А точно k раз в n испытаниях будет определяться уравнением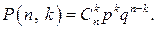 (1.79)
(1.79) означает число сочетаний из n элементов по k. Этот коэффициент называется биномиальным и определяется выражением
означает число сочетаний из n элементов по k. Этот коэффициент называется биномиальным и определяется выражением (1.80)
(1.80) (1.81)
(1.81)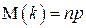 (1.82)
(1.82) (1.83)
(1.83)

 Тогда вероятность появления двух бракованных деталей из ста будет равна:
Тогда вероятность появления двух бракованных деталей из ста будет равна:
 В том случае, если вероятность появления события А очень мала, например, а количество опытов достаточно велико, можно
В том случае, если вероятность появления события А очень мала, например, а количество опытов достаточно велико, можно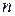 опытах определяется уравнением
опытах определяется уравнением
 (1.84)
(1.84) где
где  математическое ожидание числа
математическое ожидание числа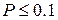 мала, то законы Пуассона и биномиальный практически совпадают, то есть можно написать уравнение
мала, то законы Пуассона и биномиальный практически совпадают, то есть можно написать уравнение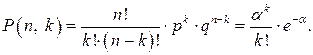 (1.85)
(1.85) формула может быть представлена в виде
формула может быть представлена в виде


 а объем выборки принимается таким, чтобы
а объем выборки принимается таким, чтобы 
 позволяет выявить линейную статистическую зависимость между двумя случайными величинами
позволяет выявить линейную статистическую зависимость между двумя случайными величинами  и
и  рисунок 1.19.
рисунок 1.19.
 );
); )
) и определяется формулой:
и определяется формулой: (1.87)
(1.87)

 . (1.88)
. (1.88) .
. необходимо проверить эту гипотезу по критерию Стьюдента. Вычисление расчетного коэффициента Стьюдента
необходимо проверить эту гипотезу по критерию Стьюдента. Вычисление расчетного коэффициента Стьюдента  осуществляется по формуле:
осуществляется по формуле: . (1.89)
. (1.89)
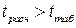 , можно принять гипотезу о значимости коэффициента корреляции. При
, можно принять гипотезу о значимости коэффициента корреляции. При  корреляционная зависимость отсутствует.
корреляционная зависимость отсутствует.





