
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Общие сведения о моделировании и математической статистикиСтр 1 из 10Следующая ⇒
Введение Одной из главных проблем теории планирования экспериментов является повышение эффективности принятия решений в области решения конкретных задач исследования различных процессов, представляющих собой сложные системы. Такие системы невозможно исследовать с помощью создания исключительно математических моделей и использования известных аналитических методов. В условиях неполного или полного отсутствия знания и понимания процессов, происходящих в объекте исследования, необходимо использовать экспериментально-статистические методы. Основой этих методов являются теория вероятностей и математическая статистика. Использование методов планирования экспериментов позволяет экспериментатору более целенаправленно и организованно решать задачи исследования объектов, достигая при этом достаточно надежных результатов. Кроме того, большим достоинством планирования экспериментов (ввиду их универсальности), является возможность использования этих методов практически в любых предметных областях. Основоположником теории планирования экспериментов считают статистика Рональда Фишера [34]. Он показал целесообразность постановки многофакторных экспериментов, то есть одновременного варьирования нескольких факторов. До этого использовались только однофакторные эксперименты. В начале пятидесятых годов возникло новое направление в области планирования экспериментов: оптимизация процессов, то есть планирование экспериментов при поиске оптимальных условий функционирования объектов исследования. Идея метода планирования оптимального эксперимента принадлежала ученым Боксу и Уилсону (P. Box, B. Wilson). Область оптимума при таком планировании достигается путем постановки серий многофакторных экспериментов. Результаты каждой предыдущей серии, после соответствующей математической обработки, позволяют выбрать условия для проведения следующей серии экспериментов. Таким образом, после целого ряда серий экспериментов, можно достичь области оптимума. Чтобы успешно справляться с задачами планирования экспериментов необходимо: 1. Хорошо знать объект исследования, например, некоторый технологический процесс. 2. На достаточно высоком уровне разбираться в математических методах планирования и обработки результатов экспериментального исследования.
3. Иметь опыт постановки экспериментов и хорошо знать и владеть компьютерными технологиями (использованием программных систем типа Mathcad, Matlab, Maple и других программных систем по статистике или пакетов прикладных программ, написанных на различных алгоритмических языках). 4. Постоянно искать и находить в различных литературных источниках новые методы и подходы теории планирования экспериментов, поскольку данная теория является довольно молодым научным направлением исследовательской деятельности. Цель данного учебного пособия состоит в том, чтобы дать читателю (студенту или аспиранту): · основы планирования экспериментов, которые в дальнейшем позволят самостоятельно продолжить изучение данной теории; · возможность самому решать практические задачи исследований с применением методов постановки и обработки результатов эксперимента. Учебное пособие снабжено большим количеством примеров практического использования рассматриваемых в нем методов планирования экспериментов.
Глава 1 Общие сведения о моделировании и математической статистики Аксиомы Колмогорова
1. 2. 3. 4. Сложение вероятностей независимых случайных событий имеет вид:
где 5. Произведение независимых случайных событий описывается уравнением
Если случайные события
где Сумма вероятностей
Измерений Измерение некоторой физической величины Q – это ее сравнение с другой величиной того же рода q, принятую за единицу измерения. Число N показывает, сколько единиц измерения q содержится в величине Q, то есть
Правая часть уравнения (1.10) называется результатом измерения. Например, при измерении некоторого расстояния в метрах, q = 1м и Q =10 м N = 10.
Измерения разделяются на два класса: 1 – прямые (непосредственные); 2 – косвенные (опосредованные). Косвенным называется измерение, полученное как результат измерения некоторых других величин и функционально связанных с измеряемой величиной. При любом процессе измерения в наличии должны быть пять необходимых факторов: 1. Объект измерения. 2. Наблюдатель, производящий измерения. 3. Измерительный прибор или приборы. 4. Используемый метод измерения. 5. Влияние внешней среды на процесс измерения [8]. Ошибки, которые всегда присутствуют в любом экспериментальном исследовании можно разделить на четыре вида: 1. Случайные, которые могут появляться в процессе проведения очередного опыта, исчезать или менять знак действия на объект исследования. 2. Систематические, которые постоянно присутствуют при проведении эксперимента или имеют тенденцию к увеличению при длительном проведении эксперимента. 3. Грубые ошибки или «промахи». Это ошибки, вызванные грубым нарушением условий проведения опыта (например, поломкой или отказом некоторой системы) или ошибкой, допущенной самим экспериментатором. 4. Методические ошибки, обусловленные выбором измерительных приборов или методом измерения. Случайные ошибки имеют шесть основных свойств [8]. 1. Свойство ограниченности. При заданных условиях измерений предельная ошибка не может превосходить некоторого предельного значения
2. Свойство компенсации. При проведении ряда измерений в одних и тех же условиях будет выполняться условие
- сумма случайных ошибок ряда измерений одинаковых условиях;
Свойство независимости. Если проводятся два ряда измерений со случайными ошибками:
то сумма попарных произведений
При выполнении условия (1.13) результаты измерений независимы. 3. Свойство рассеивания. Если ряд измерений проводится в одних и тех же условиях, то для их случайных ошибок имеет место предел
где 5. Свойство симметричности. В множестве случайных ошибок результатов измерений, полученных в одинаковых условиях, ошибки и равные по абсолютной величине, но имеющие разные знаки, встречаются практически одинаково часто. 6. Свойство унимодальности. Ошибки, большие по абсолютной величине, встречаются реже, чем меньшие. Систематические ошибки, также как случайные, обладают свойством ограниченности, то есть
где При наличии в результатах измерений постоянной систематической ошибки, сумма систематических ошибок, деленная на их число, не стремится к нулю
то есть, систематическая ошибка не обладает свойством компенсации. Такой предел может вообще не существовать, если при увеличении n арифметическая сумма
На основании свойства ограниченности (1.15) можно сделать вывод о том, что предел (1.17) ограничен неравенством
Систематические ошибки также не обладают свойством независимости, то есть
Кроме того, доказано выполнение неравенства [8]
В отношении квадратов систематических ошибок также может не выполняться условие рассеивания, можно лишь утверждать, что существует неравенство
Грубые ошибки (промахи) можно исключить из выборки наблюдений с использованием
где
Вычисляем
Если выполняется неравенство
Пример. Пусть дана выборка результатов наблюдений [24]
В этой выборке результат 20.1 будет явно сомнительным. Исключим его из выборки. Вычислим выборочное среднее
1.5. Источники и классификация ошибок численного решения задач на ЭВМ
Ошибки, которые неизбежно присутствуют при численном решении задач математического моделирования с применением ЭВМ можно классифицировать следующим образом [2]: 1) неустранимые ошибки 2) погрешность метода решения задачи 3) вычислительная погрешность Неустранимые ошибки возникают вследствие: 1) погрешностей, всегда присутствующих при получении исходных данных, по результатам экспериментов; 2) неправильного выбора математической модели объекта исследования. Неустранимыми эти ошибки называются потому, что они не могут быть устранены на последующих этапах решения задачи моделирования. Погрешность метода решения задачи моделирования обусловлена неправильным выбором способа (метода) решения данной задачи. Вычислительная погрешность возникает вследствие особенностей машинной арифметики. Эта погрешность связана с неизбежным округлением чисел при записи их в оперативную память ЭВМ, при вводе исходных данных и при выполнении арифметических операций. Необходимость округлений обусловлена особенностями представления данных в памяти ЭВМ и машинной арифметики.
Общая погрешность решения задачи на ЭВМ
Здесь
1.6. Абсолютная и относительная погрешности
Абсолютная погрешность – это разность между истинным значением некоторой величины Будет вычисляться по формуле
Абсолютная погрешность оценивается неравенством
где Относительная погрешность оценивается неравенством
где величины Х. Неравенства (1.27) – (1.28) часто используются в качестве критериев окончания работы итерационных алгоритмов.
1.7. Особенности машинной арифметики. Машинная числовая ось
Как известно, любое число (целое или действительное) можно представить в виде
В обычной арифметике это число записывается в виде
Здесь
В памяти ЭВМ целые и действительные числа, в отличие от обычной математики, представляются по-разному. Целые числа представляются в памяти ЭВМ в виде где Такое представление означает, что число имеет вид
Здесь цифра 2 является основанием системы исчисления. Двоичная система исчисления используется в настоящее время на всех современных ЭВМ. Это связано с тем, что магнитные элементы памяти ЭВМ имеют два устойчивых состояния: намагничено – 1, не намагничено – 0. Максимальное целое число, представимое в памяти ЭВМ, определяется количеством байт (восемь двоичных разрядов), которое отводится для записи целого числа с учетом знака. Совокупность нескольких байт для записи числа называется машинным словом. Если слово состоит из двух байт, то максимальное целое число
Действительные числа представляются в виде
Здесь На рисунке 1.2 показано представление действительного числа в слове памяти ЭВМ.
Рисунок 1.2. Представление действительного числа в слове ЭВМ
Величина порядка
Границы диапазона Машинная числовая ось показана на рисунке 1.3. Числа на ней расположены неравномерно, они сгущаются ближе к 0 и становятся более разреженными, приближаясь к машинным бесконечностям.
Множество чисел на машинной числовой оси не является континуумом. Это множество ограничено и называется представимым множеством Элемент
где t – число разрядов мантиссы, Разность между На представимом множестве
плавающее вычитание плавающее умножение плавающее деление Операции плавающего сложения и умножения коммутативны, то есть
(1.30)
но не ассоциативны, то есть
(1.31)
Числа Число Относительная погрешность представления – по дополнению – усечению Машинная эпсилон намного меньше Результат выполнения машинной арифметической операции имеет погрешность, приближенно равную погрешности округления:
для сложения; для вычитания; для умножения; (1.32) для деления [11].
Использование чисел с удвоенной точностью позволяет на несколько порядков уменьшить погрешность округления. Однако в этом случае вдвое увеличивается память для хранения чисел с удвоенной точностью. Операции с удвоенной точностью на современных ЭВМ реализованы на аппаратном уровне, то есть выполняются с помощью сопроцессора.
1.8. Понятие модели
Модель представляет объект исследования в некоторой форме, отличной от его реального существования. Модель дает возможность исследователю лучше понять сущность изучаемого объекта (системы), объяснить его поведение и выбрать направления дальнейшего совершенствования. Модель не может быть универсальным описанием объекта, она строится в зависимости от тех целей и задач, которые ставит перед собой исследователь. Предположим, что объектом исследования является автомобиль, то он может рассматриваться с различных точек зрения, например, доставки его от завода-производителя до автомобильного салона по продаже автомобилей. В этом случае исследователя будут интересовать только его вес и габариты. Ни какие другие качества автомобиля не будут приниматься во внимание, ни его цвет, ни его дизайн, ни его ходовые характеристики и т. п. В том случае, если исследователь будет изучать ходовые качества автомобиля, то его будут интересовать: предельная скорость движения, время разгона до нужной скорости, его устойчивость на дороге, маневренность, возможность преодолевать различные препятствия (подъемы, спуски, ямы) и т.д. При этом совершенно безразлично, какого он цвета или дизайна. Математическая модель выражает некоторые наиболее существенные свойства объекта исследования в математической форме (алгебраические и трансцендентные уравненияили системы уравнений, дифференциальные и интегральные уравнения или системы этих уравнений, уравнения в частных производных и т.д.). Модели строятся для достижения следующих основных целей: – средства осмысления действительности; – средства передачи информации; – средства обучения; – средства прогнозирования поведения изучаемого объекта в различных условиях его функционирования; – средства для постановки экспериментов. Модель может быть описательной, то есть описывающей объект исследования или его поведение в различных условиях. Предписывающая модель позволяет принимать необходимые решения для совершенствования объекта (системы) или его функционирования (например, оптимизационная модель). Математическая модель является компромиссом между бесконечной сложностью изучаемого явления (процесса, объекта) и достаточной простотой его описания. Простота описания является необходимым условием реализуемости математической модели на ЭВМ. Чрезмерное упрощение модели недопустимо, так как это может привести к потере ее адекватности изучаемому явлению. Грамотное упрощение математической модели является серьезной задачей. В то же время, упрощенная модель позволяет найти ответы на многие принципиальные вопросы и понять механизмы функционирования объекта исследования. Процесс построения модели – это интуитивное искусство. Это означает, что четких правил построения моделей не существует. В лучшем случае, есть некоторые рекомендации, которые могут оказаться полезными при построении модели.
1.9. Классификация моделей
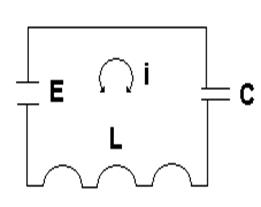
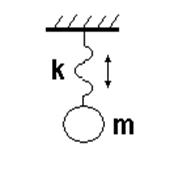
Согласно Р. Шеннону [37] типовые группы, которые могут быть положены в основу классификации моделей могут быть следующими: · Статические (в этих моделях не учитывается фактор времени). · Динамические (этими моделями описываются процессы, протекающие во времени). · Детерминированные (модели, в которых состояния объектов исследования не учитывают эффекты воздействия случайных факторов). · Стохастические (вероятностные модели, описывающие состояния системы при наличии случайных факторов). · Дискретные (описывающие объекты исследования с дискретными переменными, которые могут принимать только отдельные целочисленные значения, например, количество заготовок в схеме раскроя плитных древесных материалов, ДСтП, ДВП и т.п.). · Непрерывные (описывающие объекты исследования с непрерывными переменными, например, температура, влажность и т. д.). · Натурные, например, уменьшенные копии реальных физических объектов, имеющими с ними одну и ту же физическую природу. · Аналоговые модели, имеющие с моделируемыми объектами один и ту же закон функционирования, но разную физическую природу. Пример таких систем показан на рисунок 1.4. · Символические (математические модели, графы, чертежи и т. п.).
a) б)
Рисунок 1.4. Пример аналогового моделирования а – колебательный контур: б – маятник: Е – ЭДС, L-индуктивность, m – масса маятника, С – емкость, i – величина тока. k– коэффициент жесткости пружины.
Изменение заряда q на пластинах конденсатора, согласно второму закону Кирхгофа, описывается дифференциальным уравнением вида
Движение маятника описывается дифференциальным уравнением
Вид уравнений (1.35) и (1.36) одинаков, поэтому изменение заряда
Рисунок 1.5. Затухающие процессы
По предложению Дж. Роува [37] модели можно представить в виде целого спектра от физических моделей реальных объектов до совершенно абстрактных математических моделей, показанных на рисунок 1.6.
Рисунок 1.6. Классификация моделей по Дж. Роуву
В учебнике Пижурина А.А. и Розенблита М.С. [25] приведена другая более подробная классификация моделей объектов, рисунок 1.7. Аналитические модели строятся на основе знаний из области фундаментальных и прикладных наук (физики, математики, химии и т. д.). Эмпирические модели строятся на основе экспериментальных исследований. Блок-схемы описывают объект исследования в виде алгоритмов программ для ЭВМ.
Рисунок 1.7. Классификация моделей объектов
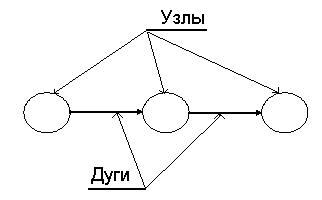
Графы описывают объект исследования в виде множества узлов (вершин) и дуг (ребер), рисунок 1.8.
Рисунок 1.8. Пример графа
Примером моделирования с помощью графов может быть транспортная задача. Модель, описывающая данную задачу, может быть представлена в виде графа, рисунок 1.9.
Рисунок 1.9. Модель транспортной задачи
Здесь
Графы могут быть направленными (ребра со стрелками) и не направленными (ребра без стрелок). В предыдущих примерах описаны направленные графы. В транспортной задаче предполагается, что существует путь от каждого пункта отправления до каждого пункта назначения. Решение транспортной задачи заключается в выборе объемов перевозки грузов Модель может представлять собой программную систему (программу) для ЭВМ. Эта модель не может быть выражена в явном виде (математической, графической, словесной или иной форме). Такая модель называется имитационной. Для имитационного моделирования разработаны специальные языки и компьютерные программные среды, реализующие эти языки (Simula, GPSS, Slam-II и т.п.). Модели классифицируются также – по отношению ко времени (статические или динамические); – по способу построения (аналитические или экспериментальные); – по степени определенности (детерминированные или стохастические). Экспериментальные модели строятся на основе результатов заранее спланированных экспериментов. Выбор модели и плана эксперимента осуществляется исследователем до его постановки. Объекты, которые подвергаются неконтролируемым или контролируемым неуправляемым воздействиям, должны описываться с помощью стохастических (вероятностных) моделей. Довольно часто процесс построения модели сочетает в себе аналитический и экспериментальный подходы. Модель строится аналитическим методом, а ее параметры определяются экспериментальным путем.
1.10. Системный подход к моделированию объектов [22]
Современная теория систем является теоретической основой многих прикладных математических и технических наук (систем управления, математических методов, экономических и т. п.). Это объясняется тем, что подходы и методы исследования в прикладных науках должны рассматриваться всеобъемлюще, то есть как комплексное решение любых актуальных задач и проблем. Тогда как многие исследователи используют локальный (ограниченный некоторыми рамками) подход к моделированию. Комплексное (системное) решение проблем учитывает всю совокупность как внешних, так и внутренних условий функционирования объектов исследования. Системный подход определяет нечто большее, чем выбор способов и методов моделирования. Это – образ мышления. Исследователь, который хотя бы раз использовал системный подход к моделированию, в дальнейшем всегда будет использовать для решения любых поставленных задач свое системное мышление. Системный подход позволяет не только описать поведение некоторой существующей системы, но и создавать новые аналогичные системы с заданным поведением. Исследователь, обладающий системным мышлением, может создавать системы с нужными ему характеристиками и заданными траекториями изменения их состояния во времени и пространстве. Системное мышление позволяет предвидеть будущее поведение системы при различных условиях ее функционирования. При таком подходе исследователь должен учитывать ситуации, которые невозможно в точности предвидеть, и иметь возможность предусмотреть действия (реакции системы) на данную ситуацию. Важнейшим понятием теории систем является ее состояние. Состояние системы может быть определено, как минимальное количество информации, необходимое для описания поведения системы в каждый данный момент времени. Например, координаты автомобиля, время и скорость по пути его следования к пункту назначения. Если известны все возможные воздействия на систему в данный момент времени, а также известны законы ее функционирования, то можно точно определить состояние системы в каждый последующий момент времени. Это безусловно относится только к системам с детерминированными (моделями) законами ее функционирования. В других системах, даже зная текущее состояние системы и величины входных воздействий на нее, невозможно точно определить ее будущие состояния. В общем виде уравнение, описывающее переходы системы из одного состояния в другое в векторно-матричной форме имеет вид
где
Для стационарных систем элементы матриц Во многих случаях невозможно непосредственно наблюдать переменные состояния, тем не менее, можно наблюдать вектор выходных величин Вектор
где
|
|||||||||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 195; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.160.61 (0.192 с.) |
 – вероятность случайного события
– вероятность случайного события  является неотрицательным числом.
является неотрицательным числом. – вероятность достоверного события
– вероятность достоверного события  равна единице.
равна единице. – вероятность невозможного события
– вероятность невозможного события  равна нулю.
равна нулю. (1.6)
(1.6) независимые случайные события.
независимые случайные события.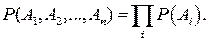 (1.7)
(1.7) являются зависимыми и событие
являются зависимыми и событие  предшествует событию
предшествует событию  (1.8)
(1.8) – условная вероятность.
– условная вероятность. равна единице
равна единице (1.9)
(1.9) (1.10)
(1.10) которое называется предельной ошибкой. Таким образом, свойство ограниченности можно представить в виде неравенства
которое называется предельной ошибкой. Таким образом, свойство ограниченности можно представить в виде неравенства (1.11)
(1.11) (1.12)
(1.12) где
где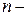 число суммируемых ошибок.
число суммируемых ошибок. ,
, (1.13)
(1.13) (1.14)
(1.14) дисперсия.
дисперсия. (1.15)
(1.15)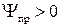 - некоторая константа, зависящая от условий измерений.
- некоторая константа, зависящая от условий измерений. (1.16)
(1.16) подвержена колебаниям, которые не приближают ее ни к какому пределу. Поэтому в общем случае, будем иметь
подвержена колебаниям, которые не приближают ее ни к какому пределу. Поэтому в общем случае, будем иметь (1.17)
(1.17) (1.18)
(1.18) (1.19)
(1.19)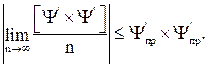 (1.20)
(1.20)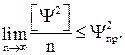 (1.21)
(1.21) критерия Стьюдента [24]. Результат измерения
критерия Стьюдента [24]. Результат измерения  , который явно не согласуется с другими результатами, то есть является сомнительным, необходимо удалить из выборки. Для других оставшихся результатов нужно вычислить среднее арифметическое
, который явно не согласуется с другими результатами, то есть является сомнительным, необходимо удалить из выборки. Для других оставшихся результатов нужно вычислить среднее арифметическое 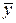 по формуле
по формуле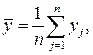 (1.22)
(1.22)
 (1.23)
(1.23) – расчетный коэффициент Стьюдента
– расчетный коэффициент Стьюдента (1.24)
(1.24) , то сомнительный элемент удаляется из выборки. В противном случае сомнительный элемент можно оставить в выборке.
, то сомнительный элемент удаляется из выборки. В противном случае сомнительный элемент можно оставить в выборке.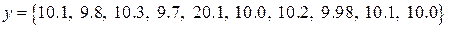 .
. , среднеквадратическое отклонение
, среднеквадратическое отклонение  ,
,  . Из таблицы коэффициентов Стьюдента при уровне значимости q=5% и числе степеней свободы f=9-1=8 возьмем табличный коэффициент Стьюдента
. Из таблицы коэффициентов Стьюдента при уровне значимости q=5% и числе степеней свободы f=9-1=8 возьмем табличный коэффициент Стьюдента  . Поскольку
. Поскольку  является грубой ошибкой и должен быть удален из выборки.
является грубой ошибкой и должен быть удален из выборки. ;
; ;
; .
. складывается из трех рассмотренных погрешностей:
складывается из трех рассмотренных погрешностей: .
.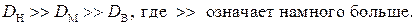
 и известным ее значением
и известным ее значением  , например, полученное в результате вычислений. Тогда абсолютная погрешность
, например, полученное в результате вычислений. Тогда абсолютная погрешность 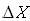
 (1.25)
(1.25) (1.26)
(1.26) заданная величина точности вычислений величины
заданная величина точности вычислений величины 
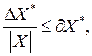 (1.27)
(1.27) – заданная величина относительной погрешности вычисления
– заданная величина относительной погрешности вычисления .
.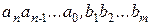 .
. – цифры от 0 до 9. Например, число 23.12 может быть представлено в виде
– цифры от 0 до 9. Например, число 23.12 может быть представлено в виде .
.
 двоичная цифра 0 или 1.
двоичная цифра 0 или 1. .
. , которое в него может быть записано, определяется по формуле
, которое в него может быть записано, определяется по формуле (здесь
(здесь  = 14).
= 14). .
. ,
,  ,
,  – число разрядов мантиссы,
– число разрядов мантиссы,  – двоичный порядок числа (
– двоичный порядок числа ( ,
,  ).
).
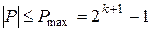 . Поэтому действительные числа могут находиться лишь в ограниченном диапазоне
. Поэтому действительные числа могут находиться лишь в ограниченном диапазоне . (1.28)
. (1.28) и
и  являются ее машинными бесконечностями (
являются ее машинными бесконечностями ( и
и 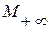 ).
).
 Рисунок 1.3. Машинная числовая ось
Рисунок 1.3. Машинная числовая ось . В этом множестве ровно
. В этом множестве ровно 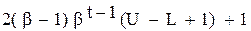 чисел.
чисел. множества
множества 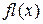 [10]. Если
[10]. Если  , (1.29)
, (1.29) =2.
=2. –м и (
–м и ( )–м представимыми числами по абсолютной величине равна
)–м представимыми числами по абсолютной величине равна  . Поскольку величина t фиксирована, то с уменьшением
. Поскольку величина t фиксирована, то с уменьшением  плавающее сложение
плавающее сложение

 не входят в представимое множество
не входят в представимое множество  , называется исчезновением порядка (антипереполнением).
, называется исчезновением порядка (антипереполнением). называется машинным эпсилон. Эта величина равняется единице первого отброшенного разряда мантиссы. В зависимости от принятого на данной ЭВМ способа округления (по дополнению или усечению) величина машинного эпсилон может иметь значения:
называется машинным эпсилон. Эта величина равняется единице первого отброшенного разряда мантиссы. В зависимости от принятого на данной ЭВМ способа округления (по дополнению или усечению) величина машинного эпсилон может иметь значения: ;
;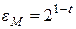 .
. , то есть
, то есть 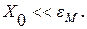

 (1.33)
(1.33) (1.34)
(1.34)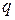 в колебательном контуре и величина
в колебательном контуре и величина 
 и
и 



 - объем запаса в пункте отправления груза (
- объем запаса в пункте отправления груза (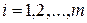 );
); - объем потребности в пункте назначения (
- объем потребности в пункте назначения ( =1,…,
=1,…, 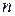 );
);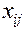 - объем перевозки груза из пункта
- объем перевозки груза из пункта  в пункт
в пункт  .
.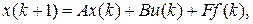 (1.35)
(1.35) вектор состояния системы в момент времени
вектор состояния системы в момент времени 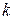 ;
; вектор состояния системы в следующий момент времени
вектор состояния системы в следующий момент времени ;
;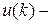 управляемый вход системы в момент времени
управляемый вход системы в момент времени  вектор влияния среды в момент времени
вектор влияния среды в момент времени  квадратная матрица размерности
квадратная матрица размерности 
 матрица размерности
матрица размерности 
 матрица размерности
матрица размерности  .
. имеют постоянные, не изменяющиеся во времени значения (константы). Стационарной называется система, в которой параметры не меняются во времени.
имеют постоянные, не изменяющиеся во времени значения (константы). Стационарной называется система, в которой параметры не меняются во времени. .
. (1.36)
(1.36) вектор состояний системы размерности
вектор состояний системы размерности  матрица размерности
матрица размерности 
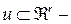 вектор входных воздействий на систему размерности
вектор входных воздействий на систему размерности  ;
;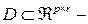 матрица размерности
матрица размерности  .
.


