Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Числовые характеристики (моменты случайной величины)
Начальные моменты · для дискретной случайной величины · для непрерывной случайной величины Начальный момент · для дискретной случайной величины · для непрерывной случайной величины Центральный момент · для дискретной случайной величины · для непрерывной случайной величины Центральный момент Дисперсия называется центральным моментом второго порядка · для дискретной случайной величины
· для непрерывной случайной величины
Дисперсия обозначается
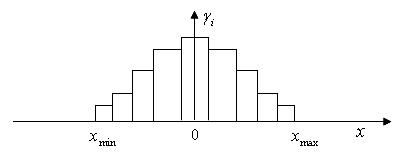
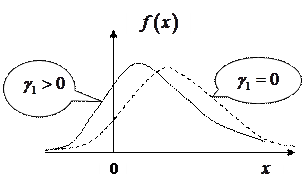
Третий центральный момент На рисунке 1.14. приведены виды распределений в дифференциальной форме с различными коэффициентами асимметрии
Рисунок 1.14. Дифференциальные формы распределений с ненулевыми коэффициентами асимметрии Величина
Рисунок 1.15. Дифференциальные формы распределений с ненулевыми коэффициентами эксцесса
Моменты существуют, если соответствующие интегралы или ряды сходятся. Для случайных величин, значения которых ограничены, моменты существуют. Нормированная случайная величина
Многие статистические таблицы распределений построены для нормированных случайных величин. Соотношения между функциями распределения ненормированных и нормированных случайных величин описываются следующими уравнениями:
Квантилем Если известны два квантиля Квантиль
Рисунок 1.16. Медиана распределения
Ордината медианы делит площадь под кривой
Квантили
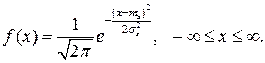
Нормальное распределение
Для нормального закона плотность распределения
Функция распределения
Теорема Ляпунова. Нормальный закон при некоторых условиях является предельным законом для суммы большого числа Нормальное распределение содержит минимум информации по сравнению с любым другим распределением с той же дисперсией. Следовательно, замена некоторого распределения эквивалентным нормальным распределением не может привести к переоценке точности наблюдений. Нормальное распределение нормированной случайной величины называется стандартным
Функция Функция Лапласа нечетная Для нормированной случайной величины
Эмпирическая функция распределения
где Теорема Гливенко. С вероятностью 1 при
(1.54) Пусть
Рисунок 1.17. Выборочная функция распределения
Все элементы выборки оказываются точками разрыва функции При обработке больших массивов данных используется метод «сгруппированных данных». Весь диапазон изменения случайной величины в выборке
с округлением до ближайшего целого. Длина интервала определяется выражением
Число элементов, попавших в Все точки, попавшие в интервал, относят к его середине
Рисунок 1.18. Гистограмма
|
||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 188; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.240.142 (0.015 с.) |
 го порядка определяются следующими формулами:
го порядка определяются следующими формулами:

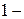 го порядка называется математическим ожиданием:
го порядка называется математическим ожиданием: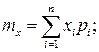
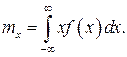
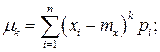
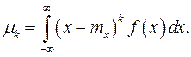

 Она характеризует поведение случайной величины в процессе проведения эксперимента. Дисперсия является центральным моментом второго порядка и определяется следующим образом:
Она характеризует поведение случайной величины в процессе проведения эксперимента. Дисперсия является центральным моментом второго порядка и определяется следующим образом: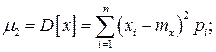 (1.43)
(1.43)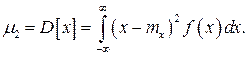 (1.44)
(1.44)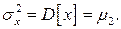 Квадратный корень из дисперсии называется среднеквадратическим отклонением или стандартом:
Квадратный корень из дисперсии называется среднеквадратическим отклонением или стандартом: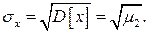 (1.45)
(1.45) , деленный на
, деленный на  называется коэффициентом асимметрии
называется коэффициентом асимметрии 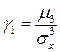 .
. .
.

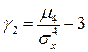 называется коэффициентом эксцесса, рисунок 1.15.
называется коэффициентом эксцесса, рисунок 1.15.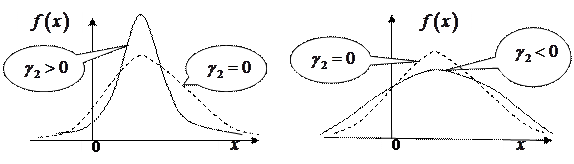

 (1.46)
(1.46) (1.47)
(1.47)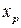 распределения случайной величины
распределения случайной величины  с функцией распределения
с функцией распределения 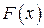 называется решение уравнения
называется решение уравнения  то есть такое значение случайной величины, что
то есть такое значение случайной величины, что 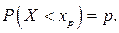
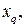 то
то 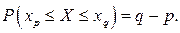
 называется медианой распределения, рисунок 1.16.
называется медианой распределения, рисунок 1.16.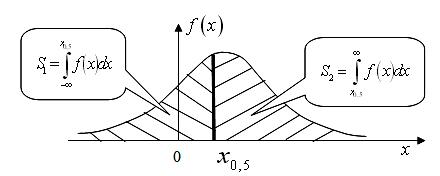
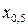
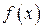 на две равные части, то есть
на две равные части, то есть  . Если распределение симметрично,
. Если распределение симметрично, 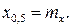
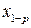 называются симметричными. Для симметричного относительно нуля распределения всегда
называются симметричными. Для симметричного относительно нуля распределения всегда 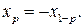
 (1.48)
(1.48)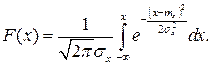 (1.49)
(1.49)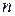 независимых случайных величин, каждая из которых подчинена какому угодно закону распределения.
независимых случайных величин, каждая из которых подчинена какому угодно закону распределения. (1.50)
(1.50) (1.51)
(1.51) называется функцией Лапласа.
называется функцией Лапласа.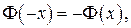 поэтому таблицы составлены лишь для
поэтому таблицы составлены лишь для 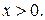
 (1.52)
(1.52) (1.53)
(1.53)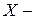 множество элементов генеральной совокупности.
множество элементов генеральной совокупности. максимальная разность между функциями распределения случайных величин
максимальная разность между функциями распределения случайных величин  стремится к нулю
стремится к нулю
 - упорядоченная по величине совокупность значений случайной величины
- упорядоченная по величине совокупность значений случайной величины  (вариационный ряд), тогда
(вариационный ряд), тогда (1.55)
(1.55)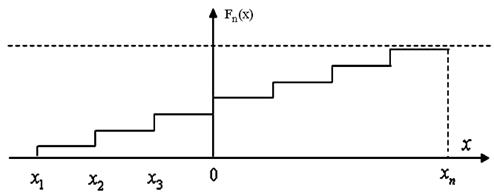
 . В точке разрыва
. В точке разрыва  функция
функция 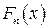 скачком переходит от значения
скачком переходит от значения  (в интервале
(в интервале 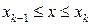 ) к значению
) к значению 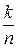 , удерживая последнее значение в следующем интервале.
, удерживая последнее значение в следующем интервале.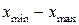 делится на
делится на 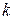 интервалов
интервалов (1.56)
(1.56) . (1.57)
. (1.57)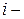 й интервал, обозначается
й интервал, обозначается 

 (1.58)
(1.58)