
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Решение дискретных задач оптимизации
В общем случае дискретный управляемый процесс можно определить как последовательность взаимосвязанных совокупностей элементов, которые можно условно обозначить вектором
Обозначим начальное и конечное состояние процесса соответственно
Математическая постановка задачи: определить
На основании выражения (3.2) можно утверждать, что величина критерия оптимизации
В связи с этим задачу оптимизации дискретной системы можно сформулировать как задачу на экстремум функции
Метод динамического программирования во многих случаях позволяет существенно сократить все затраты и определить многошаговую оптимальную стратегию. Оказывается, задачу на экстремум функции экстремум функции одной переменной
Обозначим минимальное значение критерия оптимизации на этом шаге
Затем рассматриваются два последних участка траектории с номерами
Из выражения (3.6) следует, что при оптимизации критерия на двух участках решается задача с одним переменным
При рассмотрении трех последних участков минимальное значение критерия оптимизации равно:
Для определения
Таким образом, для определения оптимальных управлений необходимо решить
…………………………………………………………………………… (3.10)
Из представленной системы уравнений (3.10) видно, что минимальное значение критерия является функцией состояния объекта, в котором он находился в начале оптимизируемого участка
Определяется оптимальное управление для всех возможных состояний объекта на каждом шаге, и для всех возможных состояний для оптимального управления вычисляется значение критерия оптимизации, которое становится весовой характеристикой данного состояния. При движении с конца траектории значение критерия в последующих состояниях определяется как минимальная сумма значения критерия предыдущего состояния и приращения критерия в течение одного шага под действием одного из допустимых управлений. Таким образом, значение критерия оптимизации в начальной точке траектории оценивает траекторию в целом. Как следует из сказанного, решение задачи требует вычислительной работы во всем пространстве допустимого рас положения оптимальной траектории. Совершенно очевидно, что чем жестче ограничения на состояние объекта, тем этих вычислений меньше и решение задачи проще. (В классических методах оптимизации имеет место обратная картина.) Как показывает практика, при большом объеме пространства состояний метод динамического программирования дает обязательный выигрыш по сравнению с методом перебора. Описанную выше вычислительную процедуру метода динамического программирования рассмотрим на примере абстрактного процесса, относительно которого известно (рис.31) начальное состояние Требуется определить оптимальную траекторию, на которой критерий оптимизации
где Так как при
Например, для рассматриваемой задачи, для узла с индексом
для узла с индексом
При этом стоимость перехода
где второе слагаемое оценивает стоимость "пути" в состояние
|
|||||||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 592; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.251.37 (0.018 с.) |
 и на которые можно разбить процесс во времени или пространстве. Составляющими вектора
и на которые можно разбить процесс во времени или пространстве. Составляющими вектора  являются элементы совокупности. Каждая совокупность элементов
являются элементы совокупности. Каждая совокупность элементов 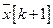 зависит только от предыдущего
зависит только от предыдущего  . Индекс
. Индекс 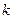 служит для нумерации состояния и может трактоваться как дискретное время или как дискретная пространственная координата (или позиция). Рассмотрим управляемые дискретные процессы, последовательность состояний которых задается уравнением связи
служит для нумерации состояния и может трактоваться как дискретное время или как дискретная пространственная координата (или позиция). Рассмотрим управляемые дискретные процессы, последовательность состояний которых задается уравнением связи (3.1)
(3.1) и
и  . Постановка задачи оптимизации имеет следующий вид: необходимо определить последовательность управлений
. Постановка задачи оптимизации имеет следующий вид: необходимо определить последовательность управлений 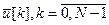 которая обеспечит за
которая обеспечит за 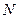 шагов перевод объекта управления из со стояния
шагов перевод объекта управления из со стояния  в состояние
в состояние 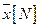 и минимизирует критерий оптимизации
и минимизирует критерий оптимизации 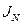 . При этом предполагается, что управляющие воздействия должны быть выбраны из допустимой области
. При этом предполагается, что управляющие воздействия должны быть выбраны из допустимой области  и промежуточные состояния процесса удовлетворяют ограничению
и промежуточные состояния процесса удовлетворяют ограничению  . В связи с тем, что процесс многошаговый критерий оптимизации вычисляется через сумму составляющих на каждом шаге:
. В связи с тем, что процесс многошаговый критерий оптимизации вычисляется через сумму составляющих на каждом шаге: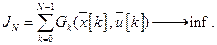 (3.2)
(3.2)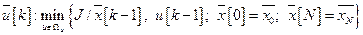
 в конечном итоге зависит только от начального состояния
в конечном итоге зависит только от начального состояния 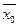 и искомой стратегии:
и искомой стратегии:
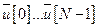 при ограничениях на управление и состояние системы. Эта задача становится трудоемкой, когда
при ограничениях на управление и состояние системы. Эта задача становится трудоемкой, когда  и
и 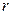 - невелико) и жестких ограничениях на величину составляющих вектора
- невелико) и жестких ограничениях на величину составляющих вектора 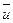 и число допустимых состояний процесса
и число допустимых состояний процесса  на каждом шаге
на каждом шаге 
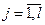 этот метод позволяет достаточно быстро определить оптимальную стратегию. Однако при увеличении размерности число возможных вариантов становится астрономически большим и их сравнение требует много времени и денежных средств.
этот метод позволяет достаточно быстро определить оптимальную стратегию. Однако при увеличении размерности число возможных вариантов становится астрономически большим и их сравнение требует много времени и денежных средств. . Идея решения вытекает из принципа оптимальности. Вся траектория движения объекта разбивается на
. Идея решения вытекает из принципа оптимальности. Вся траектория движения объекта разбивается на  ,которое действует в момент времени
,которое действует в момент времени  и переводит объект из состояния
и переводит объект из состояния  в состояние
в состояние  :
: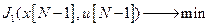 (3.4)
(3.4) тогда
тогда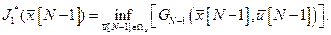 (3.5)
(3.5) . Считается, что оптимальное управление и соответствующее ему значение критерия на последнем участке известно, тогда минимальное значение критерия оптимизации на двух участках можно представить:
. Считается, что оптимальное управление и соответствующее ему значение критерия на последнем участке известно, тогда минимальное значение критерия оптимизации на двух участках можно представить: (3.6)
(3.6) , т.е.:
, т.е.: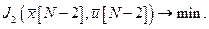 (3.7)
(3.7) (3.8)
(3.8)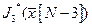 необходимо найти оптимальное управление в момент времени
необходимо найти оптимальное управление в момент времени 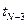 , т.е. на третьем от конца траектории участка. По аналогии минимальное значение критерия на всей траектории (
, т.е. на третьем от конца траектории участка. По аналогии минимальное значение критерия на всей траектории ( (3.9)
(3.9)
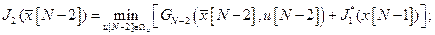

 . Поскольку при решении всей за дачи оптимизации оптимальная траектория неизвестна, неизвестны и точки
. Поскольку при решении всей за дачи оптимизации оптимальная траектория неизвестна, неизвестны и точки  . В связи с этим практическая реализация идеи, выраженной в системе (3.10), имеет следующий вид.
. В связи с этим практическая реализация идеи, выраженной в системе (3.10), имеет следующий вид.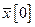 в момент времени
в момент времени  длительность протекания Т интервал дискретизации
длительность протекания Т интервал дискретизации 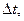 число шагов дискретизации
число шагов дискретизации  число возможных состояний - по три на каждом шаге, в том числе и при
число возможных состояний - по три на каждом шаге, в том числе и при 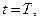 . Допустимые управления позволяют переход из каждого состояния в момент
. Допустимые управления позволяют переход из каждого состояния в момент  в каждое состояние в момент
в каждое состояние в момент  как и показано на рис.3.5.
как и показано на рис.3.5.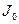 принимает минимальное значение:
принимает минимальное значение: (1.П)
(1.П) - индекс состояния системы, через который пройдет оптимальная траектория,
- индекс состояния системы, через который пройдет оптимальная траектория,  допустимых состояний два, согласно принципу Беллмана решение начинается с момента времени
допустимых состояний два, согласно принципу Беллмана решение начинается с момента времени  . Из каждого допустимого состояния временного слоя
. Из каждого допустимого состояния временного слоя  : для каждого состояния для
: для каждого состояния для  можно определить три значения критерия соответствующих двум переходам. Затем из них определяется переход с минимальным значением критерия. Этот переход отмечается(запоминается) и это состояние оценивается этим значением критерия. Для примера на рис.3 оптимальные переходы помечены жирной линией. Следовательно, в общем случае величина
можно определить три значения критерия соответствующих двум переходам. Затем из них определяется переход с минимальным значением критерия. Этот переход отмечается(запоминается) и это состояние оценивается этим значением критерия. Для примера на рис.3 оптимальные переходы помечены жирной линией. Следовательно, в общем случае величина  определяет минимальную стоимость перехода из всех возможных состояний времени
определяет минимальную стоимость перехода из всех возможных состояний времени  в состояние
в состояние 
 (2.П)
(2.П) значение стоимости перехода в этот узел:
значение стоимости перехода в этот узел: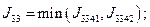
 :
: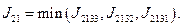
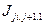 в общем случае когда критерий зависит от "пути" перехода определяется
в общем случае когда критерий зависит от "пути" перехода определяется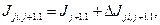 (3.П)
(3.П)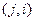 из точки
из точки  . Двигаясь с конца траектории
. Двигаясь с конца траектории  к началу, рассчитываются значения
к началу, рассчитываются значения 


