
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Приклади застосування функцій в економіці
Функції находять широке застосування в економічній теорії та практиці. Це можуть бути як найпростіші лінійні функції так і складні, що задаються рекурентними співвідношеннями. Розглянемо основні функції. 1. Функція корисності. Це залежність користі 2. Виробнича функція. Це залежність результату виробничої діяльності від обумовлюючих її факторів. 3. Функція випуску (частинний випадок виробничої функції). Це залежність об’єму виробництва 4. Функція витрат (частинний випадок виробничої функції). Це залежність витрат виробництва
5. Функція попиту, споживання та пропозиції. Це залежність об’єму попиту, споживання чи пропозиції на окремі товари та послуги від різних факторів, наприклад, ціни, прибутку тощо. Графіки функцій попиту
Всі ці функції достатньо складно виразити аналітично. При необхідності їх знаходять методами аналізу або наближають за допомогою елементарних функцій. 6. Функція податкової ставки. Це залежність податкової ставки Наведемо приклади застосування деяких функцій. Функції Торнквіста. Досліджуючи залежності попиту на різні товари від прибутку, розглянемо функції Торнквіста:
Можемо встановити рівні прибутків Графіки функції Торнквіста зображено на рис. 2.25.
Функції попиту та пропозиції. Розглянемо в одній системі координат криві попиту та пропозиції (рис. 2.26). Одержимо рівноважну (ринкову) ціну
Функції байдужості та функції бюджетного обмеження. Вивчаючи в теорії попиту криві байдужості (лінії, вздовж яких корисність двох благ
Графіками кривих байдужності є гіперболи, а графіком функції бюджетного обмеження є пряма лінія (рис. 2.27).
Границя функції Нехай функція Означення 2.7. Число При цьому припускається, що послідовність Суть цього означення полягає в тому, що, як тільки значення аргументу необмежено близько наближаються до значення Більш строгим є наступне означення границі. Означення 2.8. Число A називається границею функції Оскільки нерівність Приклад 2.6. Довести, виходячи з означення границі функції, що Розв’язання. Нехай
Очевидно, що
Якщо розглянути графік функції, зображений на рис. 2.28, то стане ясно, що ця функція не має границі при
Якщо однобічні границі функції в точці існують і рівні, то функція має границю, і вона дорівнює загальному значенню цих границь. Говорять, що границя функції при Функція
|
||||||||||||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 556; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.189.180.76 (0.008 с.) |
 деякої дії від рівня
деякої дії від рівня  , тобто інтенсивності цієї дії. Графік цієї функції зображено на рис. 2.21.
, тобто інтенсивності цієї дії. Графік цієї функції зображено на рис. 2.21.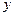 від наявності або споживання ресурсу
від наявності або споживання ресурсу  від об’єму продукції
від об’єму продукції 
 та пропозиції
та пропозиції  від ціни
від ціни  зображено на рис. 2.24 а, б.
зображено на рис. 2.24 а, б.
 в % від величини річного прибутку
в % від величини річного прибутку  ;
; ;
; .
. ,
,  ,
,  при яких розпочинається придбання тих чи інших товарів та рівні насиченості
при яких розпочинається придбання тих чи інших товарів та рівні насиченості  ,
,  для товарів першої та другої необхідності.
для товарів першої та другої необхідності.
 даного товару в умовах конкурентного ринку.
даного товару в умовах конкурентного ринку.
 та лінію бюджетного обмеження
та лінію бюджетного обмеження  , де
, де 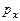 і
і  – ціни благ
– ціни благ 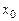 та
та 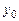 , які мають найбільшу корисність.
, які мають найбільшу корисність.
 визначена в деякому околі точки
визначена в деякому околі точки  називається границею функції
називається границею функції  , якщо для будь-якої числової послідовності значень аргументу
, якщо для будь-якої числової послідовності значень аргументу  відповідна послідовність значень функції
відповідна послідовність значень функції  прямує до числа
прямує до числа  .
. належить області визначення функції.
належить області визначення функції. можна вказати таке додатне число
можна вказати таке додатне число  , що як тільки
, що як тільки 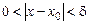 , то виконується умова
, то виконується умова  .
. визначає
визначає  можна знайти такий
можна знайти такий  , що як тільки значення аргументу
, що як тільки значення аргументу  .
.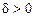 , щоб для всіх
, щоб для всіх  , виконувалася нерівність
, виконувалася нерівність або
або  .
. , оскільки при такому d умова
, оскільки при такому d умова  приводить до виконання умови
приводить до виконання умови 
 . У такій ситуації говорять про односторонні границі функції. Якщо
. У такій ситуації говорять про односторонні границі функції. Якщо  за умови, що значення аргументу прямують до
за умови, що значення аргументу прямують до 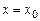 зліва, і пишуть
зліва, і пишуть  . Аналогічно, якщо
. Аналогічно, якщо  залишаючись більше
залишаючись більше  .
. можна вказати таке додатне число
можна вказати таке додатне число  . У цьому випадку пишуть
. У цьому випадку пишуть  (рис. 2.29).
(рис. 2.29). , якщо для будь-якого, скільки завгодно малого
, якщо для будь-якого, скільки завгодно малого  , можна вказати таке число
, можна вказати таке число 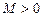 , що для всіх
, що для всіх  виконується нерівність
виконується нерівність  .
.




