
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Розділ 2. Послідовності. Функції однієї змінної
Числові послідовності Нехай кожному натуральному числу Загальний член послідовності
Наприклад, для Відмітимо, що послідовність задана, якщо зазначений спосіб одержання її членів. Виходячи з означення, послідовність завжди має нескінченну кількість елементів: будь-які два різних її елемента відрізняються принаймні своїми номерами, яких нескінченна кількість. Послідовність називається обмеженою, якщо множина її значень обмежена, тобто існує таке число Послідовність Так послідовність із загальним членом Послідовність, яка не є обмеженою (зверху, знизу) називається необмеженою (зверху, знизу). Приклад 2.1. Довести обмеженість послідовності:
Розв’язання. З очевидних нерівностей
випливає, що Приклад 2.2. Довести необмеженість послідовності:
Розв’язання. Сформулюємо заперечення означення обмеженості послідовності: Розглянемо Для Верхню (нижню) грань множини значень елементів послідовності Будемо називати послідовність зростаючою, якщо Зростаючі і спадні послідовності називають монотонними. Наприклад, послідовність
Границя послідовності Означення 2.1. Число A називається границею числової послідовності
Послідовність, яка має границю, називається збіжною. Послідовність, яка не є збіжною, називається розбіжною. Нерівність
Інтервал Означення 2.2. Послідовність Якщо Приклад 2.3. Довести, що Розв’язання. Покажемо, що для кожного, як завгодно малого, наперед заданого числа e можна підібрати такий номер З означення границі послідовності випливає, що зі збільшенням порядкового номера члени послідовності необмежено близько наближаються до своєї границі, прямують до неї, тоді пишуть: при Очевидно, якщо послідовність має границю, то вона обмежена. Слід зазначити, що зростаюча, обмежена зверху послідовність має границю. Аналогічно спадна, обмежена знизу послідовність також має границю. Приклад 2.4. Довести збіжність послідовності: Розв’язання. Застосовуючи формулу бінома Ньютона, одержимо:
Оскільки при переході від
Таким чином
Число 2,7182… називають неперовим числом на ім’я шотландського математика Джона Непера (1550-1617), а символ Означення 2.3. Послідовність Приклад 2.5. Довести, що Розв’язання. Оцінимо модуль різниці:
З останньої нерівності маємо Теорема 2.1. (Критерій Коші збіжності послідовності). Для того, щоб послідовність була збіжною необхідно і достатньо, щоб вона була фундаментальною. Означення 2.4. Послідовність Прикладами нескінченно малих послідовностей можуть бути: Наведемо властивості нескінченно малих послідовностей: 1) алгебраїчна сума скінченного числа нескінченно малих послідовностей є нескінченно малою послідовністю; 2) добуток нескінченно малої і обмеженої послідовності є нескінченно малою послідовністю; 3) добуток скінченного числа нескінченно малих послідовностей є нескінченно малою послідовністю; 4) для того, щоб число За допомогою останньої властивості можна встановити наступні властивості збіжних послідовностей: 1) якщо 2) якщо послідовності 3) якщо послідовності 4) якщо послідовність 5) якщо послідовності Наведемо твердження, які корисні при знаходженні границь: 1) якщо 2) 3) якщо
|
||||||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 539; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.174.55 (0.022 с.) |
 поставлено у відповідність число
поставлено у відповідність число  , тоді говорять, що задано числову послідовність
, тоді говорять, що задано числову послідовність  або
або  .
. . Надаючи
. Надаючи  , одержимо послідовність значень функції:
, одержимо послідовність значень функції:
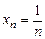 послідовність має вигляд:
послідовність має вигляд: 
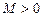 , що для всіх
, що для всіх  . Геометрично це означає, що всі члени послідовності належать інтервалу
. Геометрично це означає, що всі члени послідовності належать інтервалу  .
. , тобто нерівність
, тобто нерівність  виконується
виконується 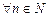 , і обмеженою знизу, якщо множина її значень обмежена знизу, тобто існує таке число
, і обмеженою знизу, якщо множина її значень обмежена знизу, тобто існує таке число  .
. є обмеженою; послідовність натуральних чисел
є обмеженою; послідовність натуральних чисел  обмежена знизу; послідовність цілих від'ємних чисел
обмежена знизу; послідовність цілих від'ємних чисел 
 обмежена зверху.
обмежена зверху. .
. ,
, 
 , тобто послідовність обмежена.
, тобто послідовність обмежена. .
.

 .
.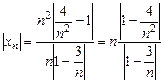 . Якщо
. Якщо  , то
, то  і
і  ,
,  , звідки
, звідки  .
. візьмемо
візьмемо  , наприклад
, наприклад  , тоді
, тоді  , звідки випливає, що послідовність необмежена.
, звідки випливає, що послідовність необмежена. (
( ).
).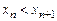 і спадною, якщо
і спадною, якщо  .
. спадна, послідовність
спадна, послідовність  зростаюча, а послідовність
зростаюча, а послідовність  не є монотонною.
не є монотонною.
 такий, що
такий, що  виконується нерівність
виконується нерівність  . Границю позначають:
. Границю позначають: 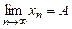 (
( є скорочення латинського слова limes, що означає “границя”).
є скорочення латинського слова limes, що означає “границя”). або
або  .
. називають
називають  –околом точки A. Виходячи з цього, можна сформулювати геометричний зміст границі послідовності: число
–околом точки A. Виходячи з цього, можна сформулювати геометричний зміст границі послідовності: число  є границею послідовності
є границею послідовності  , якщо для будь-якого, довільно обраного
, якщо для будь-якого, довільно обраного  , що всі наступні елементи послідовності (з номерами
, що всі наступні елементи послідовності (з номерами 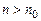 ) потраплять у
) потраплять у  виявиться лише скінченна кількість елементів послідовності.
виявиться лише скінченна кількість елементів послідовності. . В цьому випадку пишуть:
. В цьому випадку пишуть:  .
.
 (відповідно
(відповідно  ), то пишуть:
), то пишуть:  (відповідно
(відповідно  ). В усіх цих випадках кажуть, що послідовність має нескінченну границю, рівну
). В усіх цих випадках кажуть, що послідовність має нескінченну границю, рівну  ,
,  або
або  .
. .
. члена послідовності, що для всіх наступних номерів
члена послідовності, що для всіх наступних номерів  . Розв’язуючи цю нерівність, одержуємо
. Розв’язуючи цю нерівність, одержуємо  або
або  ; тобто якщо прийняти за
; тобто якщо прийняти за  , то для всіх наступних членів послідовності означення границі виконується.
, то для всіх наступних членів послідовності означення границі виконується. ,
, 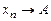 .
. .
.
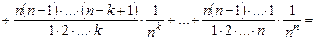

 .
. число доданків, які всі додатні, зростає і, крім того, кожен доданок збільшується. Можна записати:
число доданків, які всі додатні, зростає і, крім того, кожен доданок збільшується. Можна записати:  при
при  , то
, то 
 , маємо:
, маємо: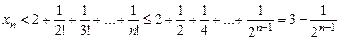 .
.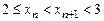 . Тобто послідовність
. Тобто послідовність  . По більш точним оцінкам можна одержати:
. По більш точним оцінкам можна одержати: .
.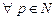
 .
. фундаментальна.
фундаментальна.
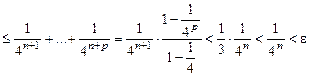 .
. ,
,  . За
. За  можна взяти, наприклад,
можна взяти, наприклад,  .
.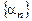 називається нескінченно малою послідовністю, якщо
називається нескінченно малою послідовністю, якщо  .
. ,
,  .
. , де
, де 
 ;
; – збіжні, то послідовності
– збіжні, то послідовності  також збіжні, і
також збіжні, і  ;
; також збіжна, і
також збіжна, і  ;
; , то послідовності
, то послідовності  також збіжна, і
також збіжна, і  ;
;
 , то послідовність
, то послідовність  також збіжна, і
також збіжна, і  .
. , то
, то  . Якщо
. Якщо  , то
, то  ;
;
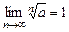 ;
; і
і  , то
, то  .
.


