
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Наближені обчислення за допомогою похідної
Теорема 3.4. Приріст функції Дійсно, використовуючи означення еквівалентних нескінченно малих, одержуємо
Тут Можна стверджувати, що при досить малих значеннях
При розв'язанні багатьох задач приріст функції заміняють її диференціалом, що, звичайно, обчислити простіше. Виходячи з наближеної рівності (3.18) можна записати, що
Остання формула дає можливість приблизно обчислити значення функції для “незручного” значення аргументу Приклад 3.10. Дана функція Розв’язання. Приймемо
Еластичність функції В багатьох економічних задачах потрібно обчислити відсоток приросту (відносний приріст) залежної змінної, відповідно відсотку приросту незалежної змінної. Це приводить до поняття еластичності функції (іноді її називають відносною похідною). Коефіцієнт еластичності показує відносну зміну досліджуваного економічного показника під дією одиничної відносної зміни економічного чинника, від якого він залежить при незмінних інших чинниках, що впливають на нього. Нехай величина
яка характеризує швидкість зміни функції зі зміною аргументу Наприклад, якщо розглянемо функцію попиту на цукор
залежить від того, чим вимірюється попит на цукор у кілограмах або в центнерах. У першому випадку похідна вимірюється в кг/грош. од., у другому – у ц/грош. од., відповідно її значення при тому самому значенні ціни буде різним залежно від одиниць виміру розміру попиту. Тому для виміру чутливості зміни функції до зміни аргументу в економіці вивчають зв'язок не абсолютних змін змінних
Введемо поняття еластичності. Нехай дана функція Функція отримає приріст
Величину Складемо відношення відносного приросту функції до відносного приросту аргументу:
Це співвідношення показує у скільки разів відносний приріст функції більше відносного приросту аргументу. Його можна записати в такому вигляді:
Якщо функцію
Одержаний результат називають еластичністю функції Означення 3.4. Еластичністю функції Еластичність позначається символом
Еластичність Приклад 3.11. Обчислити еластичність функції Розв’язання. За означенням еластичності маємо:
Якщо, Наведемо основні властивості еластичності. 1). Еластичність – безрозмірна величина, значення якої не залежить від того, в яких одиницях вимірюються величини
2). Еластичність суми двох функцій
3). Еластичність добутку двох функцій
4). Еластичність частки двох функцій
5). Еластичності взаємно обернених функцій – взаємно обернені величини:
Наприклад, еластичність величини попиту за ціною обернена еластичності ціни за величиною попиту Еластичності елементарних функцій: 1. Еластичність степеневої функції Дійсно: 2. Еластичність показникової функції
3. Еластичність лінійної функції Дійсно: Функція з нескінченною еластичністю в усіх точках називається абсолютно еластичною, з нульовою еластичністю в усіх точках – абсолютно нееластичною. Приклад 3.12. Обчислити еластичність функції Розв’язання. Нехай
|
||||||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 254; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.79.60 (0.017 с.) |
 і її диференціал
і її диференціал 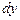 є еквівалентними нескінченно малими при
є еквівалентними нескінченно малими при  .
. .
. , оскільки
, оскільки  є нескінченно малою при
є нескінченно малою при  :
: . (3.18)
. (3.18) або
або . (3.19)
. (3.19) , замінивши його “зручним”
, замінивши його “зручним”  , при цьому у формулі
, при цьому у формулі  . Знайти приблизно
. Знайти приблизно  .
. ,
,  , тоді
, тоді  . На підставі формули (3.19) для даної функції складемо наближену рівність:
. На підставі формули (3.19) для даної функції складемо наближену рівність:  . Оскільки
. Оскільки  ,
,  ,
,  , одержимо
, одержимо .
.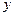 залежить від
залежить від  . Зміна незалежної змінної
. Зміна незалежної змінної  приводить згідно з функціональною залежністю до зміни змінної
приводить згідно з функціональною залежністю до зміни змінної  . Постає питання, як виміряти чутливість залежної змінної
. Постає питання, як виміряти чутливість залежної змінної  ,
, від його ціни
від його ціни  , то побачимо, що значення похідної при кожній ціні
, то побачимо, що значення похідної при кожній ціні 
 будемо називати відносним приростом аргументу.
будемо називати відносним приростом аргументу. .
. будемо називати відносним приростом функції.
будемо називати відносним приростом функції. .
. .
. .
. . Отже
. Отже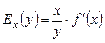 . (3.20)
. (3.20) .
. .
. , то еластичність функції дорівнює числу
, то еластичність функції дорівнює числу  . Це означає, якщо
. Це означає, якщо  %.
%.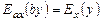 .
. .
. та
та  може бути знайдена за формулою:
може бути знайдена за формулою: .
. . Тобто:
. Тобто:
 .
.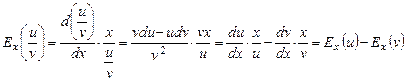 .
. .
. .
.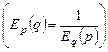 .
. стала і дорівнює показнику степеня
стала і дорівнює показнику степеня  .
. .
. пропорційна
пропорційна  . Маємо:
. Маємо: .
. :
: 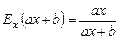 .
. .
. .
. ,
,  , тоді
, тоді ,
,  ;
; .
.


