Определение кратчайших путей в графе

Метод Форда-Беллмана

Рассмотрим ориентированные графы, ветвям которых в соответствие поставлены веса. Напомним, что в качестве весов могут выступать интересующие нас показатели эффективности (длина, стоимость, пропускная способность и т.д. Таким образом, каждой ветви поставлено в соответствие некоторое вещественное число a (x,y), называемое весом данной ветви. Если последовательность вершин v ₀, v ₁, v ₂,..., v_p определяет путь в G, то его длина определяется как сумма

Нас будет интересовать нахождение кратчайшего пути между фиксированными вершинами. Длину такого кратчайшего пути мы будем обозначать l (s,t) и называть расстоянием от s до t (расстояние определенное таким образом может быть и отрицательным). Если не существует ни одного пути из s в t то

l (s,t) = ∞.

Отметим, что если каждый контур нашего графа имеет положительную длину, то кратчайший путь будет всегда элементарным путем, то есть в пути v ₁, v ₂,..., v_p не будет повторов. С другой стороны, если в графе существует контур отрицательной длины, то расстояние между некоторыми парами вершин становится неопределенным, потому что, обходя контур достаточное число раз мы можем показать путь между заданными вершинами с длиной меньшей произвольного вещественного числа.

Расстояние в приведенном графе неопределено. В таком случае необходимо говорить о длине кратчайшего элементарного пути. Дадим практическую интерпретацию задачи о кратчайшем пути. Вес ветви может соответствовать стоимости (или времени) передачи информации между вершинами. В таком случае нас интересует самый дешевый (или самый скорый) путь доставки информации. Можно также поставить задачу о самом надежном пути. Рассматриваемые нами ниже методы дадут не сами пути, а расстояние между заданными вершинами. Однако, зная расстояние, мы можем при условии положительной длины всех контуров легко определить кратчайшие пути. Для этого достаточно отметить, что для произвольных s, t, …, v (s ≠ t) существует такая вершина v, что

l (s, t) = l (s, v) + a (v, t).

Действительно, таким свойством обладает предпоследняя вершина произвольного кратчайшего пути из s в t. Далее мы можем найти вершину u такую, что

l (s, v) = l (s, u) + a (u, v)

и т.д. Из положительности длины всех контуров легко следует, что созданная таким образом последовательность t, v, u,... не содержит повторений и заканчивается вершиной S. Очевидно, что эта последовательность и определяет путь из s в t.

Отметим, что в случае положительных весов ребер задача о кратчайшем пути в неориентированном графе легко сводится к аналогичной задаче для некоторого ориентированного графа. С этой целью достаточно заменить каждое ребро { u,v } двумя дугами [ u,v ] и [ v,u ], каждая с таким же весом, что и { u,v }. Однако в случае неположительных весов это приводит к возникновению контуров с неположительной длиной.

Алгоритм Форда - Беллмана

Большинство известных алгоритмов нахождения расстояния между двумя фиксированными вершинами s и t опирается на действия, которые в общих чертах можно представить следующим образом: при данной матрице весов ветвей А [ u,v ], u, v.. V, вычисляются некоторые верхние ограничения L (v) на расстояния от s до всех вершин v. V. Каждый раз, когда мы устанавливаем, что

L (u) + A (u, v) < L (v),

мы улучшаем оценку

L (v) = L (u) + A (u, v).

Процесс прерывается, когда дальнейшее улучшение ни одного из ограничений невозможно. Легко можно показать, что значение каждой из переменных L (v) равно тогда l (s, v) - расстоянию от s до v. Заметим, что для того чтобы определить расстояние от s до t приходится вычислять расстояние до всех вершин графа от s. Не известен ни один алгоритм нахождения расстояния между двумя фиксированными вершинами, который был бы существенно более эффективным, нежели известные алгоритмы определения расстояния от фиксированной вершины до всех остальных. Опишем теперь более детально методы нахождения расстояния от фиксированной вершины, называемой источником (его будем обозначать через s), до всех остальных вершин графа.

Сначала представим алгоритм для общего случая, в котором предполагаем только отсутствие в графе контуров с отрицательной длиной. Это алгоритм Форда - Беллмана, известный с 1956 года. Он известен также как алгоритм определения кратчайшего пути на графе методом приписывания узлам весов.

Пусть дан ориентированный граф (V, W) с n вершинами и выделенным источником. Граф задан матрицей весов дуг A (u, v) u, v … V. Граф не содержит контуров отрицательной длины. Источнику s приписываем вес l (s) = 0. Расстояние до всех остальных вершин l (s, v) = ∞, v ≠ s, v … V. Просматриваем все вершины смежные с s и понижаем их вес:

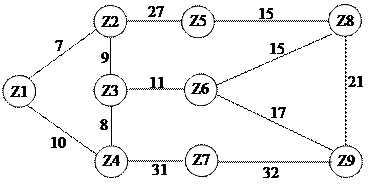
l (v) = l (s) + A (s, v).

Далее, просматривая вершины, понизившие вес, понижаем вес смежных с ними вершин:

l (u) = l (v) + A (v, u).

Процесс ведем до тех пор, пока на очередном шаге вес ни одной вершины не изменится. Проиллюстрируем работу алгоритма Форда - Беллмана.

При решении этой задачи с помощью ЭВМ необходимо пользоваться матрицей смежности, в которой веса существующих ветвей отмечаются их показателями эффективности, а все остальные элементы матрицы, соответствующие ветвям, дополняющим анализируемый граф до полносвязного берутся равными бесконечности.

Будем рассматривать алгоритм решения задачи поиска кратчайшего пути между парой узлов сети связи методом Форда-Беллмана на примере сети, топологическая структура и взвешенная матрица связности которой показаны на рис.5.16. В графовой модели топологической структуры сети вес (показатель эффективности) каждой ветви написан рядом с ветвью.

Рис. 5.16.

Таблица 5.1

Номера узлов
	∞ ∞ ∞	∞ ∞	∞	∞ ∞	∞ ∞	∞ ∞

 

Для машинного решения задачи поиска кратчайшего пути между парой узлов графа структура сети связи может быть представлена взвешенной матрицей смежности В, представленной в табл. 5.1, в которой элементы b_{i j} имеют численные значения равные весам соответствующих элементов сети. Веса ветвей, дополняющих представленную топологическую структуру сети связи до полносвязной, принимаются равными бесконечности.

Решение задачи ведется в два этапа. Первый этап решения задачи заканчивается приписыванием каждому узлу Z графа такого веса, который равен сумме весов ветвей в кратчайшем пути между узлом источником и данным узлом. На втором этапе решения задачи выявляются маршруты прохождения кратчайших путей между узлом источником и каждым узлом графа. Алгоритм первого этапа является итерационным и выполняется за конечное число шагов, которое заранее не известно.

Рассмотрим алгоритм выполнения первого этапа решения задачи поиска кратчайшего пути между парой узлов графа методом Форда-Беллмана на примере графа, представленного на рис. 5.16. Результаты, получающиеся на каждом i -м шаге первого этапа, будем заносить в i -й столбец таблицы 5.2.

На первом шаге узлу источнику приписывается нулевой вес, а всем остальным узлам графа приписываются веса равные бесконечности.

На втором шаге узлам, непосредственно связанным с узлом источником, приписываются новые веса равные весам ветвей, соединяющих их с узлом источником. Веса остальных узлов остаются без изменения, равными бесконечности.

На третьем и последующих k -ых шагах определяются новые веса узлов, связанных непосредственно с узлами, менявшими свой вес на предшествующем k -1 шаге. Новые веса таких узлов определяются по правилу

V_l = min (V_l, V_j + b_jl),

где V_l - вес узла z _l, приписанный ему на k -1 шаге;

V_j + b_jl - сумма весов узла z_j после k -1 шага и ветви между узлами z_j и z _l.

Тот шаг выполнения первого этапа, после которого ни один из узлов не изменит своего веса, является последним.

В рассматриваемом нами примере на втором шаге первого этапа решения задачи узлам z ₂, z ₃, z ₄, непосредственно связанным с узлом z ₁, приписываются новые веса, равные весам ветвей, соединяющих их с узлом z ₁. Результаты приписывания на втором шаге узлам z ₂, z ₃, z ₄ новых весов помещены в таблице 5.2.

На третьем шаге новые веса могут получить те узлы графа, которые непосредственно связаны с узлами z ₂, z ₃, z ₄, менявшими свой вес на предшествующем втором шаге.

Определим вначале новые веса узлов z ₃, z ₅, z ₆ связанных с узлом z ₂, менявшим свой вес на втором шаге.

V ₃ = min (5, 2+7) = 5.

V ₅ = min (∞, 2+10) = 12.

V ₆ = min (∞, 2+20) = 22.

Определим новые веса узлов z ₂, z ₄, z ₅, z ₆, связанных с узлом z ₃, менявшим свой вес на втором шаге.

V ₂ = min (2, 5+7) = 2.

V ₄ = min (4, 5+2) = 4.

V ₅ = min (12, 5+3) = 8.

V₆ = min (22, 5+1) = 6.

Определим новые веса узлов z ₃, z ₅, z ₆, связанных с узлом z ₃, менявшим свой вес на втором шаге.

V ₃ = min (5, 4+2) = 5.

V ₅ = min (8, 4+15) = 8.

V ₆ = min (6, 4+3) = 6.

В ходе выполнения третьего шага узлам z ₃, z ₅, z ₆ новый вес определялся несколько раз. В таких случаях этим узлам присваивается наименьший из найденных весов.

В ходе выполнения третьего шага происходило изменение весов узлов z ₅ и z ₆. Следовательно, необходимо выполнять четвертый шаг для определения новых весов узлов, непосредственно связанных с узлами z ₅ и z ₆.

Выполним действия по определению новых весов узлов z ₂, z ₃, z ₄, z ₆, непосредственно связанных с узлом z ₅, менявшим свой вес на третьем шаге.

V ₂ = min (2, 8+10) = 2.

V ₃ = min (5, 8+3) = 5.

V ₄ = min (4, 8+2) = 4.

V ₆ = min (6, 8+1) = 6.

Выполним действия по определению новых весов узлов z₂, z₃, z₄, z₅, непосредственно связанных с узлом z₆, менявшим свой вес на третьем шаге.

V ₂ = min (2, 6+20) = 2.

V ₃ = min (5, 6+1) = 5.

V ₄ = min (4, 6+3) = 4.

V ₅ = min (8, 6+9) = 8.

В результате выполнения четвертого шага первого этапа ни один из узлов не изменил свой вес и поэтому данный шаг является последним в выполнении первого этапа.

Все результаты, полученные в ходе выполнения первого этапа помещены в таблице 5.2.

При выполнении второго этапа задачи поиска кратчайших путей между парами узлов сети связи маршруты прохождения в сети искомых путей выявляются в направлении от узла-получателя к узлу-источнику.

Таблица 5.2.

Номер узла	Номер шага
	∞ ∞ ∞ ∞ ∞	∞ ∞

Из всего множества ветвей, входящих в узел-получатель, только одна ветвь принадлежит кратчайшему пути. Принадлежность каждой из ветвей, входящих в узел-получатель, к кратчайшему пути определяется по выполнению следующего правила. Ветвь принадлежит кратчайшему пути, если ее вес равен разности весов соединяемых ею узлов.

Для удобства выполнения второго этапа решения задачи представим на рис. 5.17 анализируемый граф с обозначенными рядом с каждым узлом приписанными им весами. Рядом с каждой ветвью укажем также заданные по условию задачи веса ветвей.

 

Рис. 5.17

Определим в этом графе кратчайший путь между узлами z ₁ и z ₅. В узел z ₅ входит четыре ветви, но только для одной из них, соединяющей узлы z ₃ и z ₅, выполняется условие равенства ее собственного веса с разностью весов соединяемых ею узлов.

После того как найдена конечная ветвь пути приступаем к поиску предшествующей ей ветви. Для этого должны быть проанализированы все ветви, входящие в узел z ₃. По результатам анализа выявлено, что только для ветви между узлами z ₁ и z ₃ выполняется условие равенства ее собственного веса и разности весов узлов ею соединяемых. Следовательно, кратчайший путь между узлами z ₁ и z ₅ содержит две транзитные ветви, проходит через узел z ₃ и сумма весов составляющих его ветвей равна в рассмотренном примере 8.

Одним из показателей эффективности методов поиска кратчайших путей в графе является его вычислительная сложность, т.е. количество необходимых шагов, выполняемых методом в худшем случае решения задачи (при поиске наиболее удаленной вершины графа). Метод Форда-Беллмана применим практически для любых графов, в том числе и для графов с отрицательными весами дуг, однако его вычислительная сложность О(n ³), где n - число вершин графа.

Метод Дейкстры

Пусть задана связная сеть G, в которой каждому ребру приписан положительный вес, равный длине ребра. Длина пути в такой сети равна сумме длин ребер, составляющих путь. Наша задача состоит в отыскании кратчайшего пути между двумя заданными вершинами. Один из лучших алгоритмов по критериям сложности и трудоемкости алгоритм Дейкстры (Dijkstra). Однако его применение ограничивается графами без отрицательных весов дуг или когда граф бесконтурный. Рассмотрим сущность этого алгоритма на примере. Пусть нам задан неориентированный граф G (рис.5.18) в котором мы хотим найти кратчайший путь от вершины 1 к вершине 9.

 

Рис. 5.18

Граф может быть представлен матрицей смежности A, в которой:

A (i,j) = длина ребра между вершинами i и j;

A (i,j) = ∞, если между i и j нет ребра;

A (i,i) = 0 для всех i = 1,2,..., m.

Алгоритм Дейкстры состоит из повторяемых выполнений следующих шагов:

1. Определяются непосредственные расстояния (то есть длиной в одно ребро) от заданной вершины s до всех остальных вершин.

2. Выбирается наименьшее из них в качестве «постоянного» наименьшего расстояния. Вершина, инцидентная этому ребру считается «определенной».

3. Это наименьшее расстояние добавляется к длинам ребер от «определенной» вершины до всех остальных вершин, с которыми она непосредственно соединена.

4. Полученные суммы сравниваются с предыдущим расстоянием от s до этих вершин и заменяет прежнее расстояние, если новое меньше.

5. «Определенная» вершина удаляется из списка вершин, до которых еще не определены кратчайшие расстояния, то есть список укорачивается на один элемент.

Затем этот процесс повторяется, начиная с шага 2, присоединяется новое кратчайшее расстояние к списку и т.д., пока конечная вершина t не окажется соединенной с s путем из выделенных ребер.

Работу алгоритма по шагам при поиске кратчайшего пути из вершины 1 можно представить в виде таблицы:

Таблица 5.3.

Номер шага	Номера вершин и расстояния до них
	-		∞		∞	∞	∞	∞	∞
	-	-				∞	∞	∞	∞
	-	-		-		∞		∞	∞
	-	-	-	-				∞	∞
	-	-	-	-		-
	-	-	-	-	-	-
	-	-	-	-	-	-	-
	-	-	-	-	-	-	-	-

 

Результирующее множество кратчайших расстояний показано в виде дерева кратчайших путей рис. 5.19, где числа в кружочках показывают порядок выбора ребер алгоритмом. Кратчайший путь до данной вершины отыскивается в явном виде прослеживанием пути по этому дереву из корня (1) до интересующей нас вершины.

Рис. 5.19

При поиске кратчайшего пути по таблице необходимо руководствоваться общим правилом прохождения от узла-получателя к узлу-источнику: из всего множества ветвей, входящих в узел-получатель, только одна ветвь принадлежит кратчайшему пути, у которой ее вес равен разности весов соединяемых ею узлов.

Как мы видим, в наихудшем случае задача отыскания кратчайшего расстояния из начальной вершины до конечной имеет ту же сложность, что и задача отыскания кратчайших путей из начальной вершины во все остальные вершины. Алгоритм работает итеративно и, в общем случае прекращает свою работу при достижении интересующей нас вершины. Вычислительная сложность алгоритма О(n ²).

При обсуждении алгоритма мы предполагали, что все длины неотрицательны. Алгоритм Дейкстры не применим, если какие либо из длин отрицательны (почему?). Однако некоторая модификация этого алгоритма делает его применимым для более общего случая, когда в графе нет ориентированных циклов с отрицательной длиной.

В сложных системах централизованного управления сетями связи, когда центральный узел ведет распределение информации по ветвям очень важно постоянно иметь общую картину состояния сети, знать кратчайшие пути доставки информации между всеми узлами.