
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Поиск экстремумов многомерных функций
Постановка задачи. Метод случайного поиска В ряде практических задач при проектировании различных технических систем, в том числе и сетей связи, требуется искать оптимальное решение зависящее не от одного, как было рассмотрено выше, а от нескольких параметров. В этом случае говорят о задаче многомерной оптимизации. Рассмотрим конкретный пример такой задачи. Проектируется сеть связи дивизии. Заданы: количество и места расположения узлов связи N*, количество каналов связи между узлами К*, пропускная способность V*. Требуется разработать сеть связи минимальную по стоимости С и длине линий связи L. Конечно на практике задается намного больше параметров и более конкретно, но мы ограничимся данным упрощенным вариантом для уяснения сущности задачи. Перейдем от словесной к математической постановке задачи, которую представим в следующем виде
где N - число узлов связи в сети; K - количество каналов между узлами сети связи; V - пропускная способность сети связи; N*, K*, V* - ограничения по этим показателям заданные заказчиком сети связи. Как видно из (4.4) необходимо найти такое решение, которое удовлетворяло бы одновременно всем условиям, приведенным в фигурных скобках. Причем в двух из них требуется найти минимальные значения показателей С и L. Приступим к анализу и решению задачи. На первый взгляд может показаться, что решение задачи тривиально. Следует первые три показателя в (1) поставить в рамки заданных ограничений, а два последних найти с помощью изученных методов одномерной оптимизации по отдельности. На самом деле, если более детально проанализировать от каких параметров зависят С и L, то можно увидеть, что они взаимозависимы. Чем меньше протяженность линий связи L, тем и меньше стоимость сети связи С, однако на практике на стоимость влияет не только стоимость кабеля связи, но и стоимость его прокладки по местности. А при наличии естественных препятствий: рек, гор, лесов, болот, железных и автомобильных дорог и т.п. не всегда кратчайший маршрут прокладки линии связи будет минимальным по стоимости. Таким образом, было бы логично определить функциональную зависимость этих показателей F (C, L) и искать ее минимальное значение. Так как функция F (C, L) зависит от двух переменных, то ее решение следует искать не на плоскости как для случая одномерных функций, а в пространстве. Рассмотрим чем же отличаются методы одномерного и многомерного поиска.
На первый взгляд может показаться, что различие между методами многомерного и одномерного поиска состоит в том, что первые требуют большего объема вычислений и что в принципе методы, пригодные для функций одной переменной можно применять и для функций многих переменных. Однако это не так, поскольку многомерное пространство качественно отличается от одномерного. Прежде всего с увеличением числа переменных уменьшается вероятность унимодальности целевой функции. Кроме того, множество элементов, образующих многомерное пространство, гораздо мощнее множества элементов одномерного пространства. Объем вычислений, необходимых для сужения интервала неопределенности является степенной функцией, показатель которой равен размерности пространства. Так, если при общем поиске в случае одномерного пространства для достижения f д=0,1 приходится сделать 19 вычислений целевой функции, то в случае двумерного пространства 361, трехмерного - 6859, четырехмерного - 130321, а пятимерного - 2476099! Поскольку практические задачи имеют зачастую значительно большее число переменных, серьезность трудностей, обусловленных многомерностью становится очевидной. Случайный поиск Ранее говорилось о громоздкости вычислений в случае многомерного пространства на примере числа значений целевой функции, которые необходимо вычислить, чтобы, пользуясь методом общего поиска, получить f д=0,1, и было показано, что это число растет как степенная функция, показатель степени которой равен размерности пространства. Оригинальный подход, позволяющий обойти эту трудность, предложен Бруксом и основан на случайном поиске. Пусть пространство проектирования представляет собой куб или гиперкуб со стороной, равной 1, и разделено на кубические ячейки путем деления на 10 равных частей каждой стороны куба, соответствующей одному из проектных параметров. При N =2 число ячеек равно 100, при N =3 оно равно 1000; в общем случае при N измерений число ячеек равно 10 N. Вероятность того, что выбранная наугад ячейка попадет в число 10% наиболее перспективных ячеек, равна 0,1, т.к. при N =1 нас будет интересовать одна ячейка из десяти, при N =2 одна из десяти лучших при общем количестве ячеек 100 и т.д. Вероятность того, что мы пропустим одну из 10% наиболее перспективных ячеек составит 0,9. Если случайным образом выбрать две ячейки, то вероятность пропуска будет 0,92, т.е. 0,81. Вообще вероятность нахождения по крайней мере одной ячейки из наиболее перспективных, доля которых равна f д, после N попыток составит
P = 1 - (1 - f д) N, откуда
В таблице 4.1 указано, сколько ячеек надо выбрать случайным образом, чтобы обеспечить заданную вероятность при заданной доле наиболее перспективных ячеек. Из нее видно, что при случайной выборке 44 ячеек вероятность достижения f д=0,1 составит 99%. Это совсем не плохо, если вспомнить, что для 100%-ного обеспечения целевую функцию в случае пяти переменных пришлось бы вычислить 2476099 раз. Таблица 4.1
Таким образом, сущность метода случайного поиска состоит в следующем: 1. Определяется количество вычислений N в зависимости от заданных коэффициента дробления f д и вероятности достижения цели Р. 2. Случайным образом выбираются N точек в n -мерном пространстве. 3. Вычисляются значения многомерной функции в выбранных точках. 4. Из полученных значений выбирается наилучшее по заданным критериям. Метод случайного поиска имеет два преимущества. Во-первых, он пригоден для любой целевой функции, независимо от того, является ли она унимодальной или нет. Во-вторых, вероятность успеха при попытках не зависит от размерности рассматриваемого пространства. Хотя этот метод не позволяет непосредственно найти оптимальное решение, он создает подходящие предпосылки для применения в дальнейшем других методов поиска. Поэтому его часто применяют в сочетании с одним или несколькими методами других типов. Методы прямого поиска Методы прямого поиска основываются как правило на вычислении только значений целевой функции и целенаправленном движении к оптимальному решению. Основная сложность состоит в определении направления, в котором должен вестись поиск. Все используемые методы прямого поиска используют по меньшей мере N независимых направлений поиска, где N - размерность вектора x. Элементарным примером метода, в рамках которого реализуется процедура рекурсивного перебора на множестве направлений поиска, является метод циклического изменения переменных, в соответствии с которым каждый раз меняется только одна переменная. При таком подходе множество направлений поиска выбирается в виде множества координатных направлений в пространстве управляемых переменных задачи. Затем вдоль каждого из координатных направлений последовательно проводится поиск точки оптимума на основе методов решения задач оптимизации с одной переменной. Если целевая функция обладает свойством сферической симметрии, такой поиск обеспечивает получение решения исходной задачи. Однако, если линии уровня функции искривлены или растянуты (что весьма часто имеет место в возникающих на практике задачах) то итерации могут превратиться в бесконечную последовательность уменьшающихся шагов и процедура поиска становится неэффективной. Кроме того, как показал Пауэлл, изменение координатных направлений поиска из любого заданного множества) в циклическом порядке может не только оказаться неэффективным, но и привести к отсутствию сходимости к точке локального оптимума даже при бесконечном числе итераций.
Конструктивные попытки повышения эффективности этого метода были связаны с тем обстоятельством, что поиск, периодически проводимый в направлении d (i) = x (i) - x (i -1), позволяет существенно ускорить сходимость. Это обстоятельство было положено в основу модифицированного метода, разработанного Хуком и Дживсом и являющегося одним из первых алгоритмов, в которых при определении нового направления поиска учитывается информация, полученная на предыдущем итерациях. Метод поиска Хука-Дживса По существу процедура Хука-Дживса представляет собой комбинацию «исследующего» поиска по образцу с использованием определенных эвристических правил. Исследующий поиск ориентированан на выявление характера локального поведения целевой функции и определение направлений вдоль «оврагов». Полученная в результате исследующего поиска информация затем используется в процессе поиска по образцу при движении по «оврагам». Исследующий поиск. Для проведения исследующего поиска необходимо задать величину шага, которая может быть различной для разных координатных направлений и изменяться в процессе поиска. Исследующий поиск начинается в некоторой исходной точке. Если значение целевой функции в пробной точке не превышает значения функции в исходной точке, то шаг поиска рассматривается как успешный. В противном случае необходимо вернуться в предыдущую точку и сделать шаг в противоположном направлении с последующей проверкой значения целевой функции. После перебора всех N координат исследующий поиск завершается. Полученную в результате точку называют базовой точкой. Поиск по образцу. Поиск по образцу заключается в реализации единственного шага из полученной базовой точки вдоль прямой, соединяющей эту точку с предыдущей базовой точкой. Новая точка образца определяется в соответствии с формулой xp (k +1) = x (k) + (x (k) - x (k -1)). Как только движение по образцу не приводит к уменьшению целевой функции, точка x p(k +1) фиксируется в качестве временной базовой точки и вновь проводится исследующий поиск. Если в результате получается точка с меньшим значением целевой функции, чем в точке x (k), то она рассматривается как новая базовая точка x (k +1). С другой стороны, если исследующий поиск неудачен, необходимо вернуться в точку x (k) и провести исследующий поиск с целью выявления нового направления минимизации. В конечном счете возникает ситуация, когда такой поиск не приводит к успеху. В этом случае требуется уменьшить величину шага путем введения некоторого множителя и возобновить исследующий поиск. Поиск завершается, когда величина шага становится достаточно малой. Последовательность точек, получаемую в процессе реализации метода, можно записать в следующем виде:
x (k) - текущая базовая точка, x (k -1) - предыдущая базовая точка, x p(k +1) - точка, построенная при движении по образцу, x (k +1) - следующая (новая) базовая точка. Приведенная последовательность характеризует логическую структуру поиска по методу Хука-Дживса. Алгоритм метода Хука-Дживса Шаг 1. Определить: начальную точку x (0), приращения D i, i =1,2,3,..., N, коэффициент уменьшения шага a > 1, параметр окончания поиска e > 0. Шаг 2. Провести исследующий поиск. Шаг 3. Был ли исследующий поиск удачным (найдена ли точка с меньшим значением целевой функции)? Да: перейти к шагу 5. Нет: продолжать. Шаг 4. Проверка на окончание поиска. Выполняется ли неравенство Да: прекратить поиск; текущая точка аппроксимирует точку оптимума x*. Нет: уменьшить приращения по формуле D i = D i /a, i =1,2,3,..., N. Перейти к шагу 2. Шаг 5. Провести поиск по образцу: x p(k +1) = xk + (x (k) - x (k -)). Шаг 6. Провести исследующий поиск, используя x p(k +1) в качестве базовой точки; пусть x p(k +1) - полученная в результате точка. Шаг 7. Выполняется ли неравенство f (x (k +1)) < f (x (k))? Да: положить x (k -1) = x (k) x (k) (k +1). Перейти к шагу 5. Нет: перейти к шагу 4. Поиск по методу Хука-Дживса Найти точку минимума функции f (x) = 8 x 21 + 4 x 1 x 2 + 5 x 22, используя начальную точку x (0) = [- 4, - 4] Т, Решение. Для того, чтобы применить метод прямого поиска Хука-Дживса, необходимо задать следующие величины: D x - векторная величина приращения = [1,1] Т, a - коэффициент уменьшения шага = 2, e - параметр окончания поиска = 10-4. Итерации начинаются с исследующего поиска вокруг точки x (0), которой соответствует значение функции fx (0) = 272. Фиксируя x 2, дадим приращение переменной x 1: x 2 = -4, x 1 = -4 + 1 6 f (-3,-4) = 200 < f (x (0)) ® Успех. Следовательно, необходимо зафиксировать x 1 = -3 и дать приращение переменной x 2: x 1 = -3, x 2 = -4 + 1 6 f(-3, -3) = 153 < 200 ® Успех. Таким образом, в результате исследующего поиска найдена точка x (1) = [-3, -3]T, f (x (1)) = 153. Поскольку исследующий поиск был удачным, переходим к поиску по образцу: x p(2) = x (1) + (x (1) - x (0)) = [-2,-2] T, f (x p(2)) = 68. Далее проводится исследующий поиск вокруг точки x p(2) который оказывается удачным при использовании положительных приращений переменных x 1 и x 2. В результате получаем точку x (2) = [-1,-1] T, f (x (2)) = 17. Поскольку f (x (2)) < f (x (1)), поиск по образцу следует считать успешным, и x (2) становится новой базовой точкой при следующем проведении поиска по образцу. Итерации продолжаются, пока уменьшение величины шага не укажет на окончание поиска в окрестности точки минимума x* = [0,0] T.
|
||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 1031; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.224.197 (0.03 с.) |
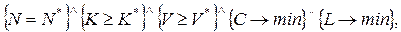

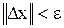 ?
?


