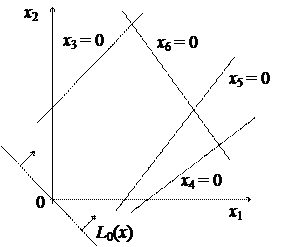Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Алгоритм поиска допустимого решения состоит в следующем.
1. Среди элементов первого столбца выбираем любой отрицательный элемент. Пусть этим элементом является b k +2. 2. В строке с выбранным отрицательным элементом находим элементы, одинаковые с ним по знаку. Пусть это будут элементы ν k +2,1 и ν k +2, m . 3. Определяем отношение отрицательного свободного члена к каждому отрицательному элементу строки и находим наименьшее из этих отношений. Пусть
Тогда столбец, в котором располагается элемент ν k +2,1 выбираем в качестве разрешающего столбца. 4. В разрешающем столбце находим элементы, одинаковые по знаку с соответствующими свободными членами (это могут быть и отрицательные элементы, если соответствующие свободные члены отрицательны). 5. Определяем отношение каждого свободного члена к соответствующему элементу разрешающего столбца. Тот элемент, разрешающего столбца, для которого отношение минимально, будет разрешающим элементом, а строка, в которой он расположен - разрешающей строкой. 6. Используя правила симплекс-преобразования, переходим к новой симплекс таблице, в которой анализируем элементы первого столбца. При наличии среди них одного или нескольких отрицательных элементов, повторяем операции по п.п.1-5. Процедура продолжается до тех пор, пока не будет найдено допустимое решение. Как только допустимое решение найдено, переходим к поиску оптимального решения, используя известный табличный алгоритм симплекс-метода. Отличие данного алгоритма от алгоритма поиска оптимального решения заключается в том, что при поиске допустимого решения анализируется не первая строка, а первый столбец симплекс-таблицы. Во всем же остальном оба алгоритма идентичны. В заключение рассмотрим случай, когда задача линейного программирования не имеет допустимых решений. Это означает, что система уравнений-ограничений несовместна, то есть не существует отрицательных переменных, которые удовлетворяли бы этой системе. Выясним, какие признаки имеет конечная симплекс-таблица при отсутствии допустимых решений. Решим для этого конкретную задачу. Задача. Найти неотрицательные значения переменных х 1, х 2,..., х 6 удовлетворяющие системе ограничений: - 5х1 + 2х2 - х3 = 10 2х1 + х2 - х4 = 8 х1 - х2 - х5 = 2 х1 + х2 + х6 = 10 и обращающие в минимум целевую функцию
L (x) = - 4 х 1 - 2 х 2 В качестве свободных переменных выберем переменные х 1, х 2. Тогда базисными переменными будут х 3, х 4, х 5, х 6. На рисунке показаны графики, соответствующие ограничениям задачи и целевой функции, построенные в координатах х 1О х 2.
Рис. 3.6 Из рисунка следует, что области допустимых решений не существует и, следовательно, задача линейного программирования не имеет допустимых решений. Приведем систему ограничений и целевую функцию к виду, удобному для заполнения симплекс-таблицы: х 3 = -10 - (5 х 1 - 2 х 2) х 4 = - 8 - (-2 х 1 - х 2) х 5 = - 2 - (- х 1 + х 2) х 6 = 10 - (х 1 + х 2)
L (x) = 0 - 4(x 1 + 2 x 2) Поиск допустимого решения в соответствии с алгоритмом приводит к следующей последовательности симплекс-таблиц: Таблица 3.5 Таблица 3.6 Таблица 3.7
В строке при переменной х 3 в таблице 3.7 свободный член отрицателен. В соответствии с п.2 алгоритма поиска допустимого решения в этой строке необходимо найти элементы, одинаковые по знаку со свободным членом. Но такие элементы в строке отсутствуют. Запишем аналитическое выражение базисной переменной:
Очевидно, что не найдется таких неотрицательных значений переменных х 3, х 4, х 5, при которых уравнение (3.27) было бы справедливым. А это означает, что задача линейного программирования не имеет допустимых решений. Таким образом, если в симплекс-таблице один или несколько элементов первого столбца отрицательны, и хотя бы в одной строке, соответствующей одному из этих элементов, остальные элементы положительны, задача линейного программирования не имеет допустимых решений.
Транспортная задача Существует определенный класс задач линейного программирования, которые по постановке несколько отличаются от обычной задачи ЛП. Соответственно и методы решения таких задач могут быть иными. К классу таких задач относится так называемая транспортная задача.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 602; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.104.214 (0.006 с.) |
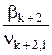 <
< 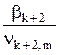 .
.