
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Операции над матрицами. Обратная матрица. Ранг матрицы
Над матрицами можно производить следующие операции: умножение на число, сложение, умножение матриц и нахождение обратной матрицы. Первые две операции называются линейными. Определение. Произведением матрицы A размера m´n на число l, называется матрица B=lA размера m´n, каждый элемент bij которой равен laij. Пример 1. Определение. Суммой матриц A и B одинакового размера называется матрица C=A+B того же размера, каждый элемент cij которой равен aij+bij. Пример 2. Матрицы разного размера складывать нельзя. Эти операции обладают свойствами: а) коммутативности (A+B=B+A), б) ассоциативности ((A+B)+C=A+(B+C)), в) дистрибутивности (l(A+B)=lA+lB). Операцию умножения матриц определим в два этапа. Определение. Произведением строки A из n элементов на столбец B из n элементов называется число AB, равное сумме произведений соответствующих элементов строки и столбца, т.е.
Строку и столбец разной длины перемножать нельзя. Пример 3. Определение. Произведением матрицы A размера m´n на матрицу B размера n´k называется матрица C размера m´k, каждый элемент cij которой равен произведению i –ой строки матрицы A на i –ый столбец матрицы B, т.е.
Пример 4. Пусть
Мы видим, что AB¹BA, т.е. умножение матриц свойством коммутативности не обладает. Единичная матрица E играет роль единицы при умножении на квадратную матрицу, т.е. для любой квадратной матрицы A верно равенство
AE=EA=A.
Произведение матриц соответствующих размеров обладает свойствами: а) ассоциативности A (BC)=(AB) C; б) дистрибутивности A (B+C)=AB+AC и (B+C) A=BA+CA. Кроме того, для квадратных матриц |AB|=|A|×|B|, т.е. определитель произведения матриц равен произведению их определителей. Определение. Обратной матрицей для квадратной матрицы A называется такая матрица A-1, что выполняется равенство A×A-1=A-1×A=E. Определение. Квадратная матрица A, определитель которой равен нулю, называется вырожденной, матрица, определитель которой не равен нулю, называется невырожденной. Пример 5. Матрица Из соотношения |A|×|A-1|=|E| = 1 следует, что у вырожденной матрицы не может быть обратной (0×|A-1|¹1). Определение. Присоединённой матрицей для квадратной матрицы A называется матрица
Пример 6. Пусть A11=(–1) 1+1×4=4, A12=(–1) 1+2×3= –3, A21=(–1) 2+1×2= –2, A22=(–1) 2+2×1=1,
Теорема об обратной матрице. Невырожденные матрицы и только они имеют обратные матрицы, которые находятся по формуле
(Здесь Пример 7. Найдём обратную матрицу для матрицы Поскольку
Сделаем проверку.
A- т.е. AA-1= A-1A=E. Обратная матрица обладает следующими свойствами: Если A и B невырожденные матрицы, то (A-1)-1=A, (AB)-1= B-1 A-1, |A-1|=|A|-1.
Ранг матрицы
Рассмотрим одну числовую характеристику любой (необязательно квадратной) матрицы. Ранг матрицы определяет число так называемых базисных строк или столбцов матрицы, через которые с помощью линейных операций можно получить все остальные строки или столбцы матрицы. Определение. Минором k -го порядка матрицы A называется определитель, составленный из элементов стоящих на пересечении произвольно выбранных k -столбцов и k-строк этой матрицы. Пример 8. У матрицы
9 миноров 1-го порядка –
Миноров других порядков у этой матрицы нет.
Определение. Рангом матрицы A называется наибольший из порядков ее миноров, не равных нулю. Он обозначается символом r(A) или rangA. r (A) – целое неотрицательное число, не превосходящее числа строк и столбцов матрицы A. Ранг нулевой матрицы считается равным нулю. Для нахождения r (A) формально необходимо рассмотреть все миноры A, начиная с 1-го порядка и проверить их на вырожденность.
Метод окаймляющих миноров позволяет сократить эту процедуру. Он состоит в следующем. Выбираем любой невырожденный минор 1-го порядка (ненулевой элемент матрицы A). Обозначим его через M1. Затем рассматриваем все миноры 2-го порядка, содержащие M1 (окаймляющие его). Если все они вырождены, то r (A)=1, если нет, то невырожденный минор 2-го порядка обозначаем через M2 и так далее. Если у матрицы A есть невырожденный минор k-го порядка и все окаймляющие его миноры (если они есть) вырождены, то r (A)=k, иначе выбираем минор Mk+1 и продолжаем этот процесс.
Пример 9. Найдём ранг матрицы У матрицы выбираем невырожденный минор 1-го порядка M1=(a11)=1. Среди окаймляющих его миноров есть один невырожденный Рассмотрим ещё один метод нахождения r (A), который называется методом элементарных преобразований или методом Гаусса. Элементарными преобразованиями для матрицы A называются следующие её преобразования. 1. Перестановка строк или столбцов местами. 2. Умножение строки или столбца на ненулевой коэффициент. 3. Прибавление к одной строке или столбцу матрицы другой её строки или столбца, умноженной на некоторое число 4. Зачёркивание нулевой строки или столбца матрицы. Матрица B, полученная из A с помощью элементарных преобразований, называется эквивалентной ей и обозначается в виде A~B.
Теорема. При элементарных преобразованиях ранг матрицы не изменяется. Теорема. Ранг треугольной матрицы равен количеству ее ненулевых строк. Метод Гаусса состоит в том, что с помощью элементарных преобразований матрица A приводится к верхнетреугольному виду с ненулевыми элементами на главной диагонали (если матрица не квадратная, то она приводится к ступенчатому виду). Число этих ненулевых элементов совпадает с рангом матрицы. Этот метод состоит в следующем. 1. С помощью перестановок строк и столбцов матрицы добиваемся того, чтобы a11 стал отличным от нуля (здесь и в дальнейшем элементы всех матриц будем обозначать в виде aij). 2. Прибавим ко второй строке первую, умноженную на 3. С помощью перестановок строк и столбцов, начиная со второй строки и второго столбца, добиваемся того, чтобы a22¹0. 4. Прибавим к третьей строке вторую, умноженную на Этот процесс продолжаем до тех пор, пока возможно получение Окончательно, после зачёркивания нулевых строк матрица приводится к виду Поскольку её невырожденный минор r – го порядка находится в левом верхнем углу, то r (A) совпадает с числом ненулевых строк получившейся матрицы. Перестановку строк или столбцов местами будем обозначать символом ↕, где стрелки указывают на переставляемые строки или столбцы, а третье элементарное преобразование символом (k), где стрелка начинается у строки, которую умножаем на k и заканчивается у изменяемой строки.
Пример 10. Найдём ранг матрицы
Проведём элементарные преобразования согласно методу Гаусса.
~ Определение. Базисным минором называется любой из отличных от нуля миноров матрицы А, порядок которого равен r (A). Пример 11. Для следующей матрицы А ее ранг равен 2:
так как существует минор 2-го порядка
Понятие ранга тесно связано с понятием линейной зависимости (независимости) её строк и столбцов. В дальнейшем материал излагается для строк матрицы, для столбцов матрицы изложение аналогично. В матрице А обозначим её строки следующим образом:
Две строки матрицы называются равными если равны их соответствующие элементы: Арифметические операции над строками матрицы (умножение строки на число, сложение строк) вводятся как операции, проводимые поэлементно:
Строка е называется линейной комбинацией строк
Строки матрицы
где 0=(0 0 …0). Линейная зависимость строк матрицы означает, что хотя бы одна строка матрицы является линейной комбинацией остальных. Действительно, пусть для определенности в формуле
где Таким образом, строка Если линейная комбинация Теорема о ранге матрицы. Ранг матрицы равен максимальному числу её линейно независимых строк или столбцов, через которые линейно выражаются все остальные её строки (столбцы). Пусть матрица А размера
тогда строки матрицы Строки Покажем, что любые (r+1) строк матрицы линейно зависимы, т.е. любая строка выражается через базисные. Рассмотрим минор (r+1)-го порядка, который получается при дополнении рассматриваемого минора элементами ещё одной строки i и столбца j:
Этот минор равен нулю, так как ранг матрицы равен r, поэтому любой минор более высокого порядка равен нулю. Раскладывая его по элементам последнего (добавленного столбца, получаем) Разделив последнее равенство на
где Фиксируем значение i (i>r) и получаем, что для любого j (j=1,2, …, n) элементы i- ой строки
Пример 12. В примере 10 для матрицы
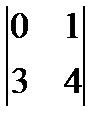
минор второго порядка
невырожден, т.е. он является базисным. Поэтому у матрицы A базисными являются 1-ая и 2-ая строки и 1-ый и 2-ой столбцы. Третью строку матрицы можно записать в виде линейной комбинации базисных строк с коэффициентами 1 и 1: (3 5 7)=1(0 1 2)+1(3 4 5). Третий столбец записывается в виде линейной комбинации первых
двух с коэффициентами (–1) и 2:
|
||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 479; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.58.169 (0.077 с.) |
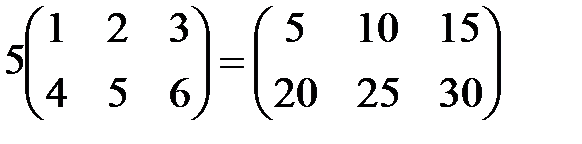

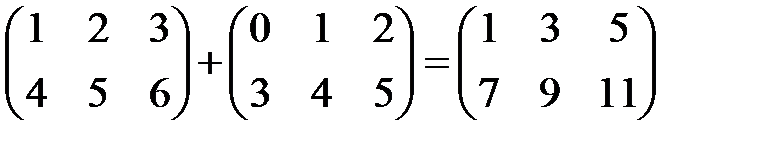
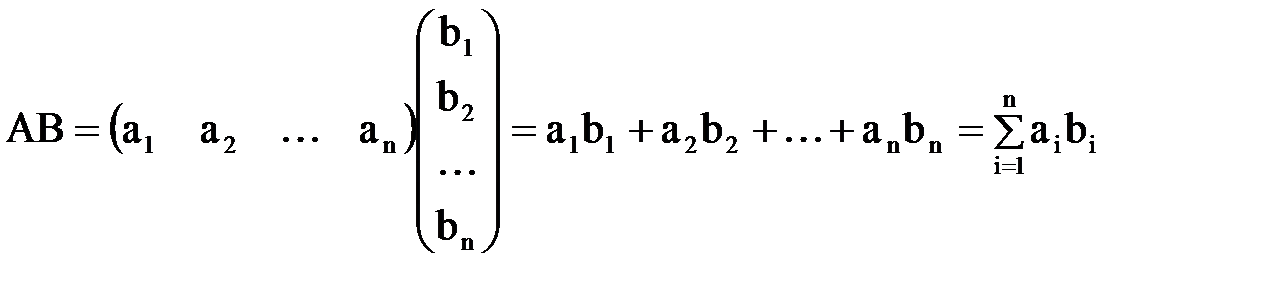
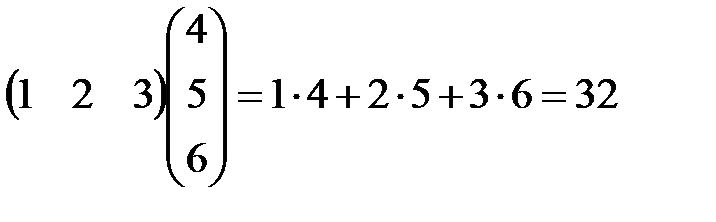
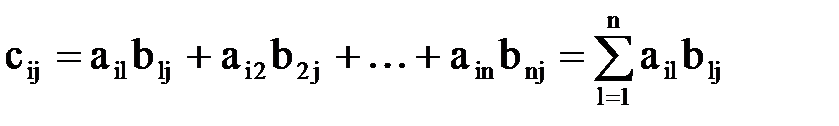
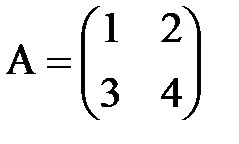 ,
, 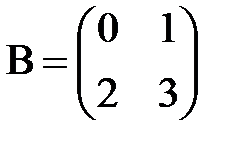 . Найдём матрицы AB и BA.
. Найдём матрицы AB и BA.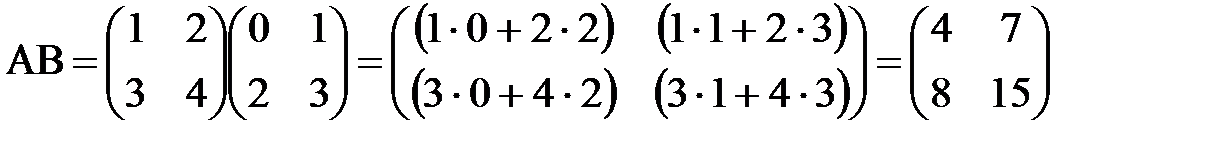
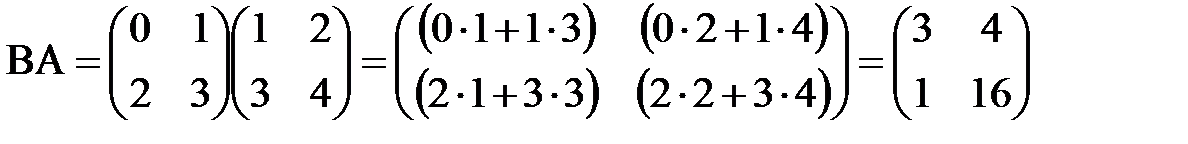
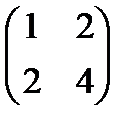 – вырождена,
– вырождена, 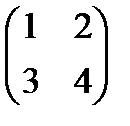 – невырождена.
– невырождена.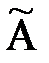 , элементами которой являются алгебраические дополнения соответствующих элементов матрицы A, т.е.
, элементами которой являются алгебраические дополнения соответствующих элементов матрицы A, т.е.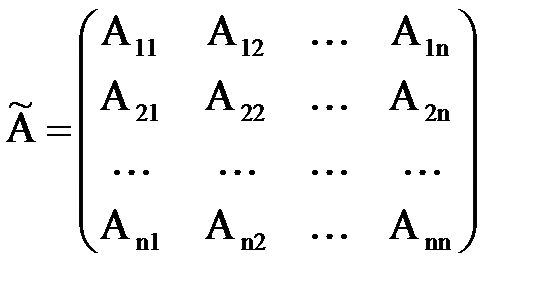
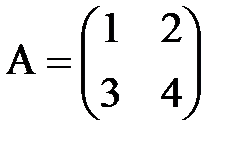 , тогда
, тогда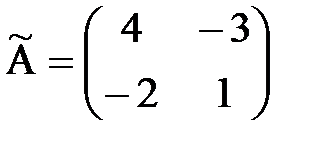
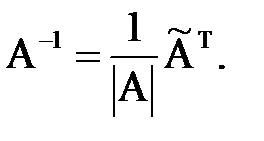
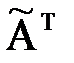 – присоединённая транспонированная матрица).
– присоединённая транспонированная матрица).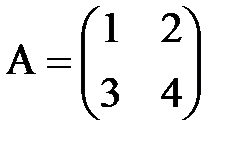 .
.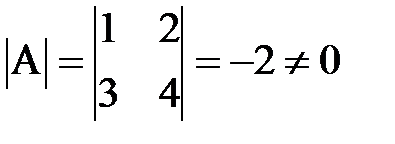 , то обратная матрица существует. В предыдущем примере мы получили, что
, то обратная матрица существует. В предыдущем примере мы получили, что 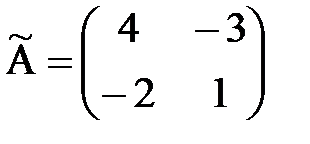 , поэтому
, поэтому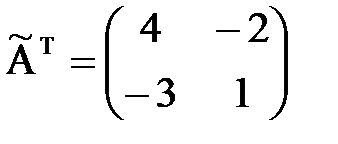 и
и 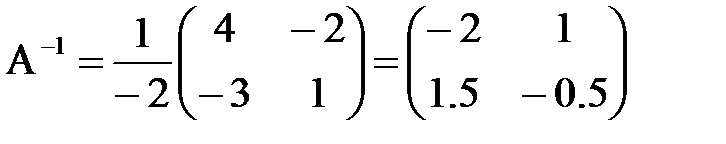 .
.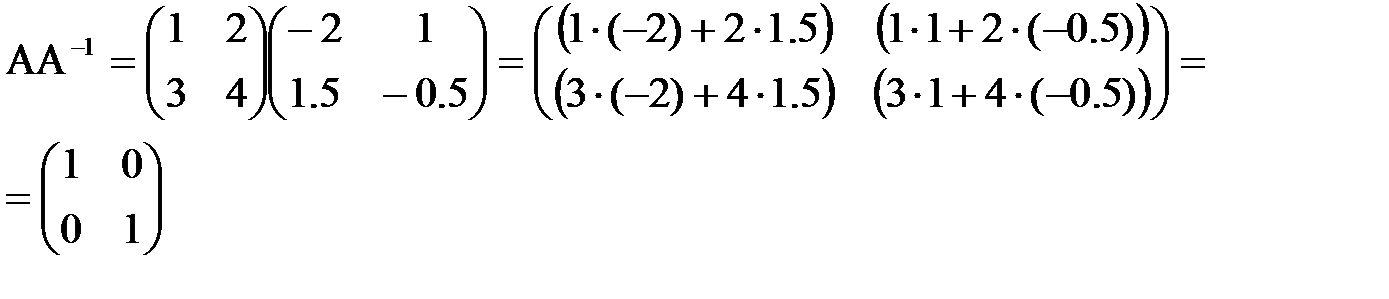
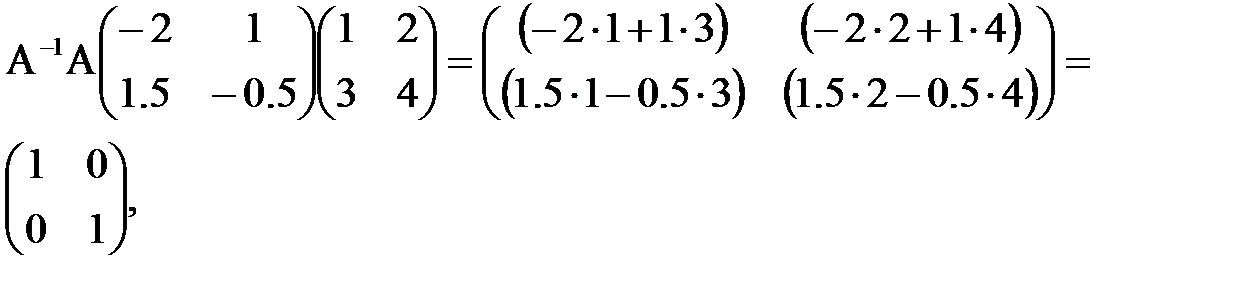
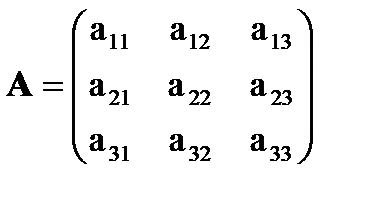 имеется один минор 3-го порядка–
имеется один минор 3-го порядка– 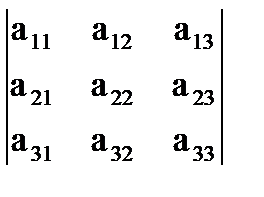 , 9 миноров 2-го порядка –
, 9 миноров 2-го порядка – 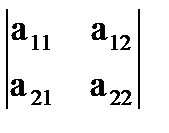 ,
, 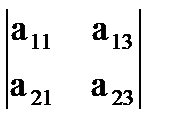 ,
,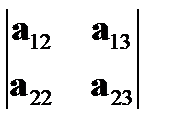 ,
, 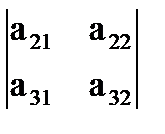 ,
, 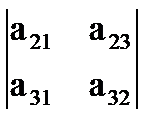 ,
, 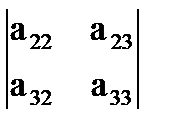 ,
, 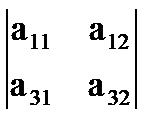 ,
, 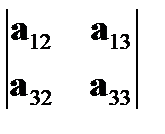 ,
, 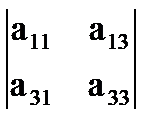 ,
,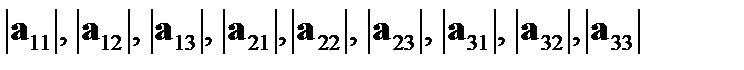 .
.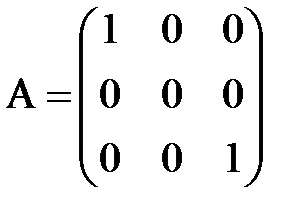 .
.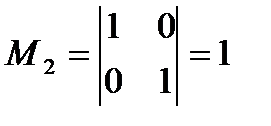 . Единственный минор 3-го порядка окаймляющий M2 – это сама матрица A. Но, поскольку
. Единственный минор 3-го порядка окаймляющий M2 – это сама матрица A. Но, поскольку 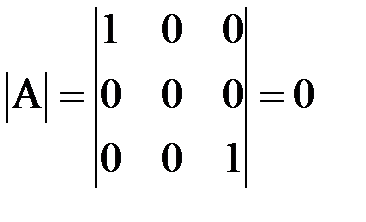 , то A – вырождена и r (A)=2.
, то A – вырождена и r (A)=2.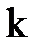 .
.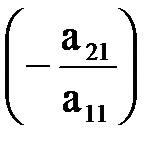 . Прибавим к третьей строке матрицы первую, умноженную на
. Прибавим к третьей строке матрицы первую, умноженную на 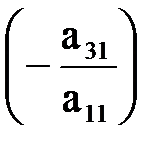 и так далее. В результате в первом столбце получим нулевые элементы ниже a11.
и так далее. В результате в первом столбце получим нулевые элементы ниже a11.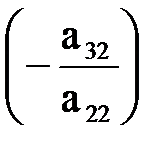 . Прибавим к четвёртой строке матрицы вторую умноженную на
. Прибавим к четвёртой строке матрицы вторую умноженную на 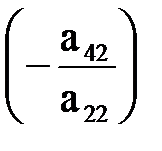 и так далее. В результате во втором столбце получим нулевые элементы ниже a22.
и так далее. В результате во втором столбце получим нулевые элементы ниже a22.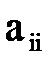 ¹0 из строк и столбцов начиная с номера i.
¹0 из строк и столбцов начиная с номера i.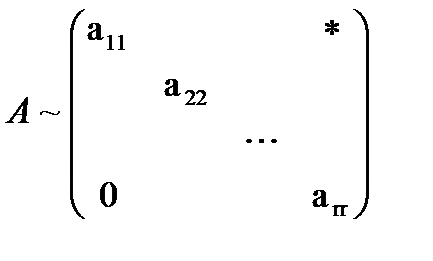 , где
, где 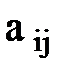 ¹ 0.
¹ 0.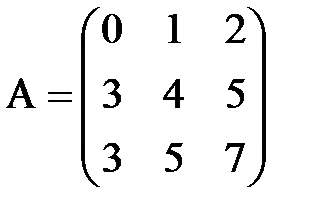 .
.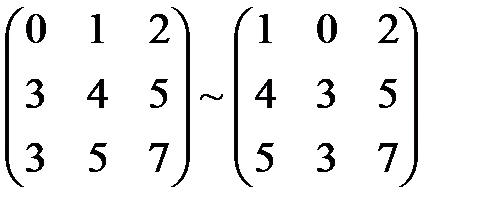
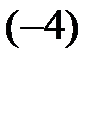
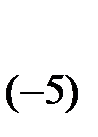 ~
~ 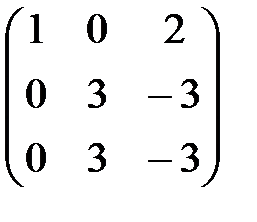
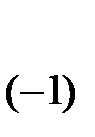 ~
~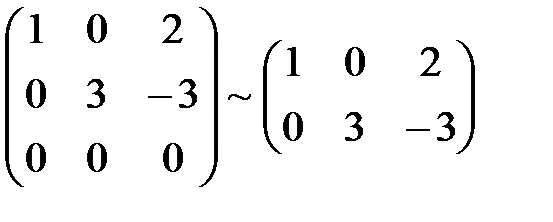
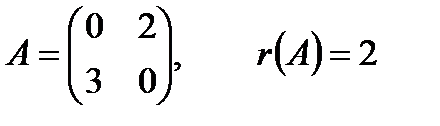 ,
,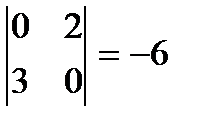 , не равный нулю, а миноров 3-го порядка у матрицы А нет. Единственный базисный минор матрицы А – минор
, не равный нулю, а миноров 3-го порядка у матрицы А нет. Единственный базисный минор матрицы А – минор 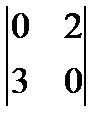 .
.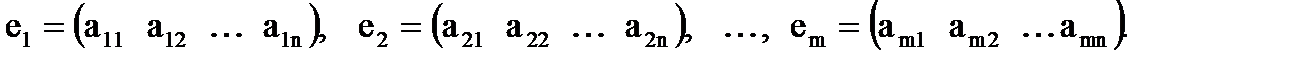
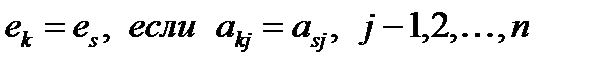 .
.

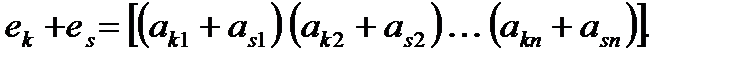
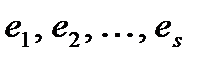 матрицы, если она равна сумме произведений этих строк на произвольные действительные числа:
матрицы, если она равна сумме произведений этих строк на произвольные действительные числа: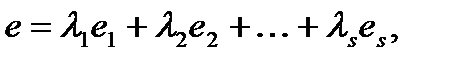
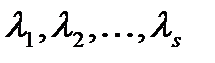 - любые числа.
- любые числа.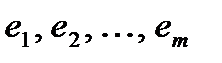 называются линейно зависимыми, если существуют такие числа
называются линейно зависимыми, если существуют такие числа 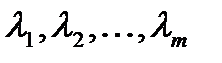 , не равные одновременно нулю, что линейная комбинация строк матрицы равна нулевой строке:
, не равные одновременно нулю, что линейная комбинация строк матрицы равна нулевой строке: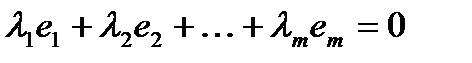
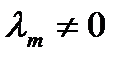 , тогда
, тогда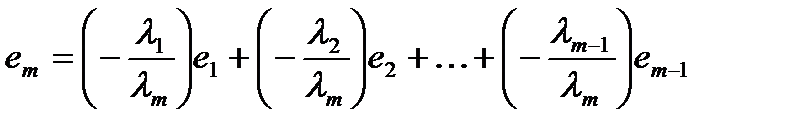 или
или 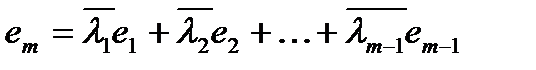
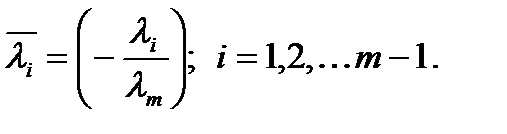
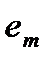 является линейной комбинацией остальных строк.
является линейной комбинацией остальных строк.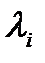 равны нулю, т.е.
равны нулю, т.е. 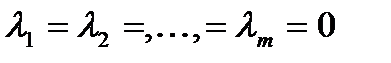 , то строки
, то строки 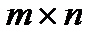 имеет ранг r (
имеет ранг r (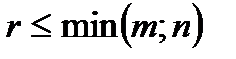 ). Это означает, что существует отличный от нуля минор r -го порядка. Всякий ненулевой минор r -го порядка называли базисным минором. Пусть для определенности это минор
). Это означает, что существует отличный от нуля минор r -го порядка. Всякий ненулевой минор r -го порядка называли базисным минором. Пусть для определенности это минор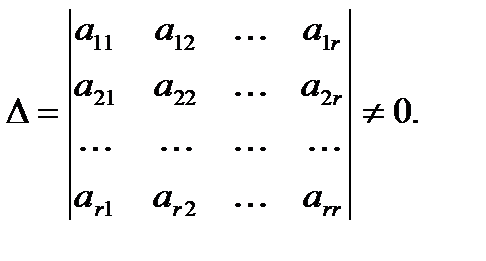
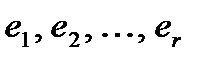 линейно независимы.
линейно независимы.
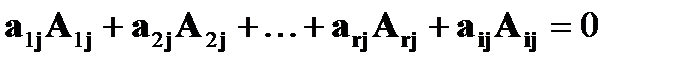 , где последнее алгебраическое дополнение
, где последнее алгебраическое дополнение 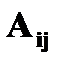 совпадает с базисным минором
совпадает с базисным минором  и поэтому отлично от нуля, т.е.
и поэтому отлично от нуля, т.е. 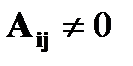 .
.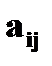 как линейную комбинацию:
как линейную комбинацию: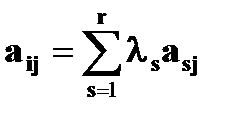
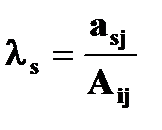 .
.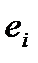 линейно выражаются через элементы строк
линейно выражаются через элементы строк 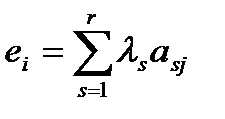 .
.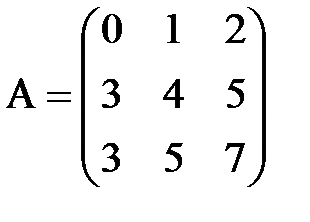
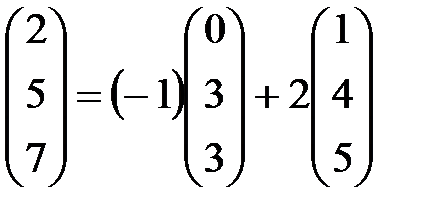 .
.


