
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Векторное произведение векторов и его свойства.
Это произведение определено только для пространственных векторов Определение. Векторным произведением векторов а) Модуль вектора
в) с) Тройка векторов
Пример 1. Найдем Поскольку Вектор
Отметим следующие свойства векторного произведения.
антикоммутативно, т.е. для любых векторов
:
Теорема. Пусть в базисе Тогда в этом базисе
Для запоминания этой формулы используется её запись в виде условного определителя:
который необходимо разложить по первой строке.
Пример2. Из того, что Пример3. Пример4. Пусть Найдем Из-за некоммутативности векторного произведения правила тождественных преобразований для этого произведения не применяются, для вычисления модуля вектора используются свойства и определения этого произведения.
Пример5. Пусть Найдем
Векторное произведение, в частности, применяется для нахождения координат векторов, перпендикулярных двум заданным векторам. В последнем примере вектор Отсюда получаем следующее.
Следствие 1. Площадь параллелограмма, построенного на векторах
Площадь треугольника, построенного на этих векторах, равна:
Пример6. Найдем площадь треугольника АВС, где Для её нахождения используем векторы
Следствие 2. Площадь параллелограмма, построенного на векторах
Площадь треугольника, построенного на векторах, равна:
Эти формулы получаются из формул следствия 1 путем подстановки туда Получим: Последнюю формулу можно такие записать в виде:
Другие приложения векторного произведения будут рассмотрены в 11-м модуле, изучаемом в третьем семестре.
|
||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 149; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.191.22 (0.009 с.) |
 и
и  , и оно обозначается символами
, и оно обозначается символами  или
или 
 и
и 
 , удовлетворяющий трём условиям:
, удовлетворяющий трём условиям: равен произведению модулей векторов
равен произведению модулей векторов  sin
sin 
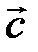 перпендикулярен векторам
перпендикулярен векторам  правая (см. рис. 2.18).
правая (см. рис. 2.18).



 .
. и
и  то
то 
 перпендикулярен векторам
перпендикулярен векторам  , т.е. он направлен вдоль оси
, т.е. он направлен вдоль оси 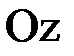 и образует правую тройку с векторами
и образует правую тройку с векторами 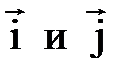 . Этим свойством обладает только вектор
. Этим свойством обладает только вектор 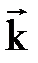 , т.е.
, т.е. .
.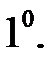 В отличие от скалярного произведения, векторное произведение
В отличие от скалярного произведения, векторное произведение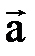 и
и  верно:
верно: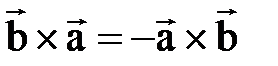 .
. . Ненулевые векторы
. Ненулевые векторы  коллинеарны только в том случае, когда
коллинеарны только в том случае, когда  .
.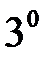 . Постоянный множитель можно выносить за знак векторного произведения, т.е. для любых векторов
. Постоянный множитель можно выносить за знак векторного произведения, т.е. для любых векторов  и числа
и числа  верно
верно .
.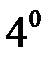 . Векторное произведение обладает свойством дистрибутивности, т.е. для любых векторов
. Векторное произведение обладает свойством дистрибутивности, т.е. для любых векторов  верно
верно 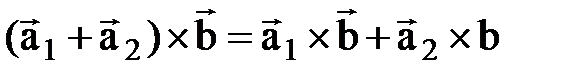 .
. векторы
векторы 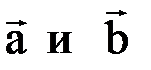 имеют координаты
имеют координаты  и
и 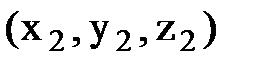 соответственно.
соответственно.
 ,
,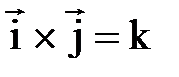 следует, что
следует, что 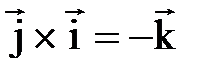 .
. .
.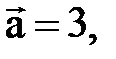
 ,
, 


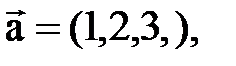

 .
.
 перпендикулярен векторам
перпендикулярен векторам 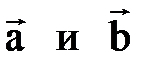 и образует с ними правую тройку. Другое приложение векторного произведения связано с задачей нахождения площадей. Заметим, что модуль векторного произведения
и образует с ними правую тройку. Другое приложение векторного произведения связано с задачей нахождения площадей. Заметим, что модуль векторного произведения 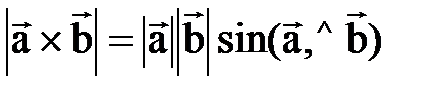 равен площади параллелограмма, построенного на векторах
равен площади параллелограмма, построенного на векторах  . Площадь треугольника образованного этими векторами равна
. Площадь треугольника образованного этими векторами равна 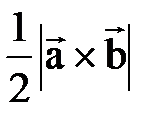
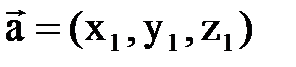 и
и  , равна:
, равна: .
.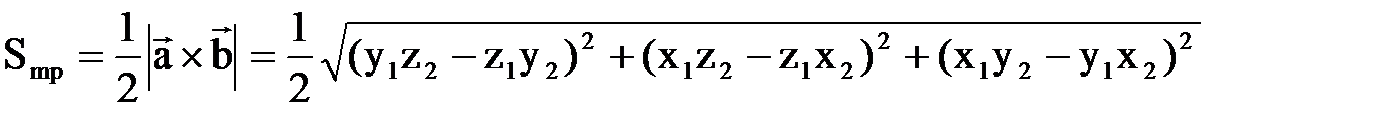 .
.
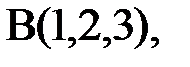

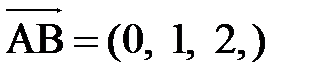 и
и 

 и
и 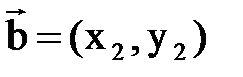 , лежащих в плоскости
, лежащих в плоскости 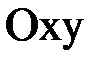 , равна:
, равна: .
. 
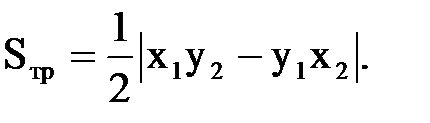
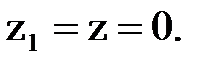
 .
. .
.


