
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Функция Грина для краевой задачи с уравнением Пуассона. Её построение методом отображений.
(1) Воспользуемся формулой: В качестве w выберем любую гармоническую функцию в D, такую что: Вычитая два этих выражения, получаем: Функция Грина является решением задачи (1),
Функция Грина задачи Её физический смысл. Рассмотрим заряд величины Функция Грина в двухмерном случае: 7. Функция Грина для задачи с уравнением
Функцией Грина будем называть решение следующей задачи: (4’) a) решение задач с её помощью Пусть
т.о. можно написать, что: b) Построение функции Грина в одномерном случае на отрезке
Рассмотрим интервал Выбираем решение
Рассмотрим интервал Пусть тогда
Из теории ОДУ знаем, что Сделаем эту постоянную
с) Функция Грина симметрична по своим аргументам G(P,Q) = G(Q,P)
|
|||||||||||||||
|
Последнее изменение этой страницы: 2017-02-06; просмотров: 572; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.141.6 (0.005 с.) |
 Точка р принадлежит области D, ограниченной контуром Г.
Точка р принадлежит области D, ограниченной контуром Г. , мы не знаем, как находится
, мы не знаем, как находится  и, соответственно, не можем найти точное решение - избавимся от слагаемого, которое её содержит. Воспользуемся второй формулой Грина для функций
и, соответственно, не можем найти точное решение - избавимся от слагаемого, которое её содержит. Воспользуемся второй формулой Грина для функций 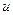 и
и  . Из второй формулы Грина следует
. Из второй формулы Грина следует 
 .
. , то есть мы выбираем её так, чтобы на границе она совпадала с
, то есть мы выбираем её так, чтобы на границе она совпадала с  .
. . Пусть
. Пусть  , тогда:
, тогда: 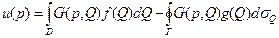 ,
,  - функция Грина задачи Дирихле.
- функция Грина задачи Дирихле. . Проинтегрируем по шару:
. Проинтегрируем по шару:
 применим теорему Гаусса
применим теорему Гаусса 
 , т.о.
, т.о.  можно определить аксиоматически:
можно определить аксиоматически:
 , это решение следующей задачи:
, это решение следующей задачи:  .
. в точке р, его потенциал в точке Q:
в точке р, его потенциал в точке Q:  , функция
, функция 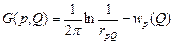 . Мы получили решение задачи (1) через функцию Грина, но саму функцию Грина не нашли, для этого надо решить задачу для
. Мы получили решение задачи (1) через функцию Грина, но саму функцию Грина не нашли, для этого надо решить задачу для  принадлежит области
принадлежит области  , ограниченной
, ограниченной  . Ищем
. Ищем  виде потенциала:
виде потенциала:  подбираем точки
подбираем точки  , сажаем в них заряды
, сажаем в них заряды  , так чтобы суммарный потенциал на границе был = 0 – метод электростатических изображений.
, так чтобы суммарный потенциал на границе был = 0 – метод электростатических изображений.  .
. , понятия, определения.
, понятия, определения. - гармоническая везде, кроме точки
- гармоническая везде, кроме точки  , в ней она имеет особенность. Рассмотрим более обобщённый случай.
, в ней она имеет особенность. Рассмотрим более обобщённый случай.  - краевая задача – общий вид – с эллиптическим уравнением.
- краевая задача – общий вид – с эллиптическим уравнением. .
. , воспользуемся второй формулой Грина, её можно применять для
, воспользуемся второй формулой Грина, её можно применять для  :
:  . Перепишем эту формулу для нашего случая:
. Перепишем эту формулу для нашего случая:  .
.
 - решение (1’) с учётом краевых условий.
- решение (1’) с учётом краевых условий. ) задача (4’) будет иметь вид:
) задача (4’) будет иметь вид:

 , её решение – функция Грина:
, её решение – функция Грина: 

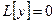
 уравнения
уравнения 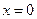 . Этих решений много. Общее решение:
. Этих решений много. Общее решение:  , где
, где  ,
,  - есть функция
- есть функция  . Это решение существует везде на отрезке
. Это решение существует везде на отрезке  .
. - решение уравнения
- решение уравнения  , Этих решений много. Общее решение:
, Этих решений много. Общее решение:  , где
, где  ,
,  - есть функция
- есть функция 
 . Интегрируем:
. Интегрируем:  , пусть
, пусть  , тогда
, тогда

 , т.о. т.о. получили уравнение, связывающее две неопределённые константы. Второе уравнение можно получить, приравняв два решения в точке разрыва:
, т.о. т.о. получили уравнение, связывающее две неопределённые константы. Второе уравнение можно получить, приравняв два решения в точке разрыва:  . Имеем систему однородных линейных уравнений для нахождения
. Имеем систему однородных линейных уравнений для нахождения  и
и  , решаем:
, решаем:  , где определитель Вронского:
, где определитель Вронского: 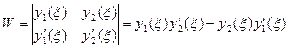 , мы можем построить не бесконечную и непрерывную функцию Грина.
, мы можем построить не бесконечную и непрерывную функцию Грина.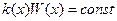 , докажем:
, докажем:  , чтд.
, чтд. выбором
выбором  и
и  .
. 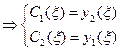 , и тогда функция Грина:
, и тогда функция Грина: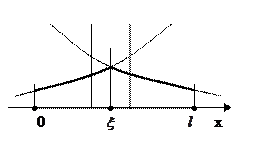
 . Излом первой производной соответствует
. Излом первой производной соответствует  -функции.
-функции.
 - линейные функции.
- линейные функции.



