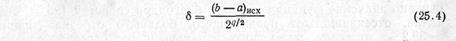Поиск оптимума численными методами

Численные методы поиска применяют, во-первых, когда в точке экстремума отсутствуют производные. Так, изменение целевой функции может носить дискретный характер, например, при срав­нении разных вариантов оформления процесса, когда Rменяется не непрерывно, а скачком от одного варианта к другому. Но про­изводные в точке экстремума могут отсутствовать и у непрерывной функции. Чаще всего это бывает, если экстремум расположен на краю области допустимых значений. На рис. 23.1 максимум лежит на краю области, в этой точке производная отсутствует. Имеется «производная слева», но она не равна нулю.

Рис 23.1 График, иллюстрирующий оптимум на краю области допустимых значений

а, b - границы области допустимых значений.

 

Часто бывает и так, что целевая функция в точке экстремума дифференцируема, но задана она таким образом, что продифферен­цировать ее в общем виде не удается, вследствие чего приходится обращаться к численным методам. Это обычно связано с тем, что функция задана не формулой, а алгоритмом вычисления при за­данных значениях аргументов (факторов). Если бы не было и алгоритма, функция была бы невычислимой и следовало бы при­менить экспериментальную оптимизацию.

Наконец, иногда имеется принципиальная возможность запи­сать и решить систему

но соответствующие вычисления столь громоздки, что численный метод оказывается проще.

В наиболее общем виде численные методы сводятся к тому, что вычисляется ряд значений R при различных значениях аргументов; сопоставление этих значений показывает, в каком направлении нужно двигаться в пространстве факторов, чтобы приближаться к оптимуму. В подавляющем большинстве случаев эти методы не дают теоретически точных значений координат оптимума. Но практически это и не нужно — нам всегда достаточно знать эти координаты с задаваемой точностью.

Оптимизация перебором применяется, если число возможных вариантов конечно. Тогда достаточно рассчитать целевую функ­цию для всех этих вариантов и выбрать наибольшее (или наимень­шее) значение. Например, мы можем рассчитать R для случаев протекания процесса в аппаратах всех стандартизованных разме­ров и выбрать лучший вариант.

Перебор легко осуществляется на ЭВМ, причем все варианты (например, нормали) могут быть заранее записаны в памяти ма­шины. Несмотря на крайнюю простоту метода, он часто оказывает­ся чрезвычайно эффективным, поскольку возможности перебора для машины несоизмеримо выше, чем для человека. Применение перебора позволяет найти такие варианты, до которых без нее дойти практические невозможно.

Сканирование — метод, близкий к перебору, но применяемый к непрерывным функциям.

Рассмотрим для примера одномерное сканирование — случай, когда ищем максимум функции от одного фактора (как мы уже говорили, поиск минимума осуществляется точно так же). Будем считать, что мы задались пределами изменения фактора х от а до Ь. Здесь а и b — ограничения, которые можно установить в любой реальной задаче: никогда не бывает так, что мы может задать лю­бые, ничем не ограниченные значения х.

Таким образом, вначале мы знаем следующее. Имеется интер­вал [а, b], на котором мы хотим отыскать экстремум целевой функции; его называют интервал неопределенности.

При этом практически нам не нужно определить точку экстре­мума абсолютно точно. Достаточно сильно сузить интервал неопре­деленности. Например, если мы узнаем, что оптимальная темпера­тура, соответствующая максимуму целевой функции, заключена в пределах от 380 К до 381 К, то большая точность не нужна. В про­мышленных условиях вряд ли удастся регулировать температуру с точностью выше 1 К. Нас устраивает интервал неопределенности [380, 381], и дальнейшее его сужение смысла не имеет.

Итак, в одномерном случае (k = 1) задача поиска экстремума сводит­ся к сужению интервала неопределенности. Методом сканирования эта задача решается так.

Выберем целое число q — число значений целевой функции, которое придется рассчитывать. Рассчитаем интервал Dx:

Отложим от точки а до точки b интервалы Dx; (рис. 25.1). Кон­цы каждого интервала назовем узлами; на рис. 25.1 каждый узел обозначен крестиком

В каждом узле рассчитаем R (х) (см. точки на рис. 25.1). Теперь мы можем принять за максимум наибольшее из полученных значений — на рисунке это 4-я точка слева. К концу расчета интер­вал неопределенности d составит 2Dx: истинный максимум может лежать либо справа, либо слева от полученной наилучшей точки (пунктиры на рис. 25.1). Таким образом

Формула (25.2) определяет эффективность метода. При сканировании для достижения достаточно малого d величина q должна быть велика. Метод малоэффективен. Но он удобен для первоначального исследования функции, поскольку дает возмож­ность представить ее вид на всем отрезке, установить число экстре­мумов и их локализацию.

Сканированием можно исследовать и функции более чем одно­го фактора. Так, участок на плоскости (факторное пространство для двух факторов) можно покрыть сетью узлов и таким образом исследовать поведение функции на этом участке. В принципе это возможно в любом k -мерном пространстве, но по мере роста k резко растет число необходимых расчетов и падает эффектив­ность метода.

Другие методы поиска более эффективны, но не обладают той универсальностью, которой отличается сканирование. Их эф­фективность связана с тем, что это — методы направленно­го поиска, в которых не просто исследуется область фактор­ного пространства, но происходит продвижение в этом пространст­ве в сторону искомого экстремума. Но направленность поиска требует соблюдения некоторых условий, ограничивающих приме­нимость методов.

Прежде всего, направленный поиск дает надежный результат, если функция унимодальна. Наиболее просто (хотя и не впол­не строго) унимодальную функцию можно определить так. В до­пустимой области она имеет только один экстремум нужного знака (один максимум, если ищем максимум, один минимум в противо­положном случае). Например, на рис. 25.2 функция 1 унимодальна. Функция 2 унимодальна, если ищем максимум, и неунимодальна при поиске минимума (два минимума —при х = а и при х = b). Функция 3 неунимодальна.

Методы направленного поиска способны привести в точку од­ного из экстремумов, но не позволяют установить, единственный ли это экстремум, а если известно, что не единственный, то в какой экстремум мы попали: глобальный (экстремальный для всей об­ласти) или локальный (другие точки могут оказаться выше в слу­чае максимума или ниже для минимума). Если при решении за­дачи оптимизации появится подозрение, что мы встретились с неунимодальностью, следует грубо исследовать функцию скани­рованием и выделить область глобального экстремума.

Еще одно важное свойство функции R, учитываемое при выборе метода поиска, — это число факторов. Здесь различаются два основных случая. Первый, когда R зависит только от одного фактора, R — R(x): тогда говорят об одномерном поиске. Второй, когда факторов больше одного — многомерный поиск. При­чем почти все методы многомерного поиска принципиально при­менимы при любом числе факторов k>1, тогда как при k = 1 при­меняются иные, одномерные методы. Лишь немногие методы, как например, сканирование, применимы и в одномерном, и в много­мерном случаях.

 

Методы одномерного поиска

Дихотомия. Как и при описании сканирования, рассмотрим поиск максимума на отрезке [а, b], показанном на рис. 25.3. Разделим отрезок пополам - точка л (левая) на рисунке. Рассчитаем значение R = R(л) в этой точке. Пока мы еще ничего не можем сказать об экстремуме, кроме того, что он принадлежит нашему отрезку.

Теперь выберем малое приращение фактора, равное е, и поставим на отрезке правую точку п=л+е. Рассчитаем R(n). Теперь, поскольку R(л)>R(п), как изображено на рис. 25.3, можно утверждать, что, если R(х) унимодальна, то максимум находится в левой половине отрезка.

Проделаем теперь следующее. Отбросим правую половину отрезка (на ней максимума нет). Для этого правый конец - точку b- перенесем в точку л. Сделаем это так. Точку л обозначим через b (такая операция не вполне привычна для традиционной математики, но в алгоритмических языках она чрезвычайно распространена). На рис. 25:3 этот перенос обозначен стрелкой. (Разумеется, если бы было R(л)<R(п), то в точку л мы перенесли бы точку а).

После того, как правый конец отрезка перенесен, задача вернулась к исходным условиям: задан отрезок от а до b, на котором нужно найти максимум. Поэтому проводится следующий цикл расчета, ничем не отличающийся от предыдущего, кроме значения b. Снова делим пополам отрезок, снова ставим вспомогательную точку на расстоянии е, снова переносим в середину либо правый, либо левый конец. Такой алгоритм (расчет слагается из одинаковых циклов, различающихся лишь начальными условиями) называют итерационным.

В принципе итерации можно проводить до бесконечности: делить пополам все меньшие отрезки. Поэтому в любом итерационном алгоритме нужно задать правило останова, определяющее, когда можно прекращать расчет, т. е. считать, что полученная точность уже достаточна. Например, можно остановить итерации, когда интервал неопределенности окажется меньше е:

Эффективность алгоритма дихотомии определяется так: каждая пара расчетов (точки лип) уменьшает отрезок [а, b ]вдвое. Обозначим исходный отрезок индексом исх. Если сделать q расче­тов (q — четное), то

 

Золотое сечение. Пропорция золотого сечения (деления от­резка в среднем и крайнем отношении) определяются так. Разделим отрезок длины l на две части: т и l — т так, чтобы меньшая часть относилась к большей, как большая ко всему отрезку

Легко сосчитать, что

Рассмотрим опять отрезок [а, b ], на котором нужно найти максимум (рис. 25.4).

Поиск максимума начинаем с того, что делим отрезок слева и справа в отношении золотого сечения — получаем точки л и п. Расстояние от а до л составляет ~ 0,382 (b-а), от а до п ~ 0,618 (b -а). В этих точках рассчитаем значение R. Как и в методе дихотомии, здесь имеем две точки л и п; но, в отличие от дихотомии, расстояние между ними не мало, и вероятность, что точка экстремума попадет между ними, достаточно велика. Поэтому, например, если R (п)>R(л) (рис. 25.4), то нельзя сказать, где окажется максимум — он может быть и в средней части отрезка (левый пунктир на рисунке), и в правой (правый пунктир). Но в левой части (мы приняли, что функция унимодальна) максимума быть не может. Поэтому можно ее отбросить — перенести левый конец отрезка в точку л, назвав ее а (левая стрелка). Теперь задача как будто вернулась к исходной формулировке: найти максимум на отрезке [а, b ]. Но на этом отрезке уже есть точка (точка п рис. 25.4), в которой рассчитано значение функции, причем, благодаря свойству (25.5), эта точка, отсекавшая от предыдущего, большего отрезка справа ~38,2%, отсекает от нового, уменьшенного отрезка справа ~61,8%, т.е. и на новом отрезке она является точкой золотого сечения. Теперь, на новом этапе расчета мы можем назвать ее л (см. правую стрелку на рис. 25.4) и поставить на уменьшенном отрезке не две точки для расчета R, а только одну - правую (на рис. 25.4 обозначена треугольником). Таким образом, на каждом этапе расчета, кроме самого первого, мы должны рассчитывать R только в одной точке, что повышает эффективность метода.

В качестве правила останова можно воспользоваться формулой (25.3).

Эффективность метода определяется следующим образом. После двух первых расчетов R и после каждого последующего остаю­щийся интервал неопределенности составляет 0,618 предыдущего, тогда при q расчетах целевой функции

При q<4 эффективность метода золотого сечения ниже, чем метода дихотомии; при небольших q, порядка 10, эффективность обоих методов близка, но при q>20 золотое сечение становится намного эффективнее. Таким образом, если не нужно очень точно фиксировать абсциссу оптимума, то можно пользоваться любым из этих методов. Если нужна высокая точность (или если каждый расчет громоздок), предпочтительнее метод золотого сечения.

Пример 25.1. Сравнение эффективности методов.

Желательно определить положение экстремума на интервале [0,1] с точностью до 0,001 длины исходного интервала неопределенности.

Формулы (25.2), (25.4) и (25.6)

показывают, что при сканировании для этого потребуется провести ~2000 расчетов функции R, при использовании дихотомии ~20 расчетов, а при использовании метода золотого сечения ~16 расчетов.

 

Методы многомерного поиска

 

Это случай, когда R — функция более, чем одного фактора (k>1).

Рассмотрим вариант, поиска максимума функция R=f(х₁,х₂), зависящей от 2^х факторов (этот случай можно изобразить на графике), без установки ограничений, поскольку ограничения вно­сят заметные усложнения в алгоритмы поиска, а сущность методов при этом, как правило, не изменяется.