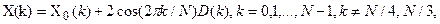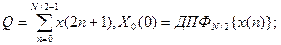Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Алгоритми швидкого перетворення Фур’є комплексної послідовності
Основна ідея алгоритмів швидкого перетворення Фур’є комплексної послідовності (ШПФк) полягає в збалансованому рекурсивному використанні методики зведення однієї задачі більшої розмірності до задач меншої розмірності. В найпростішому випадку, коли N=2m, де m=1,2,..., N-точкове дискретне перетворення Фур’є (ДПФ) зводиться до двох N/2-точкових, кожне з яких в свою чергу замінюється двома N/4-точковими і т.д. до одержання двоточкових ДПФ. На даний час розроблені різні методи побудови алгоритмів ШПФ [4]. Нижче розглянемо найвживаніші при апаратній реалізації. Алгоритми ШПФ комплексної послідовності за основою два. Існують два варіанти формул переходу до двох ДПФ меншої розмірності, які отримали назву формул розкладу (ФР) алгоритму ШПФ. В першому з них, що отримав назву алгоритму ШПФк за основою два з часовим прорідженням (ШПФк2t), ФР задається виразом.
X(k)=X1(k)+ X2(k), k=0,1,...,N-1, де X1(k)=ДПФN/2{x(n)}, X2(k)=ДПФN/2{x(2n+1)}.
В другому варіанті, що отримав назву частотного (ШПФк2f), N-точкове ДПФ замінюється двома N/2 точковими ДПФ наступним чином[4]:
де x1(n)=x(n)+x(n+N/2), x2(n)=[x(n)-x(n+N/2)].
Обидві форми алгоритмів еквівалентні з точки зору кількості обчислень, вони відзначаються простотою структури.
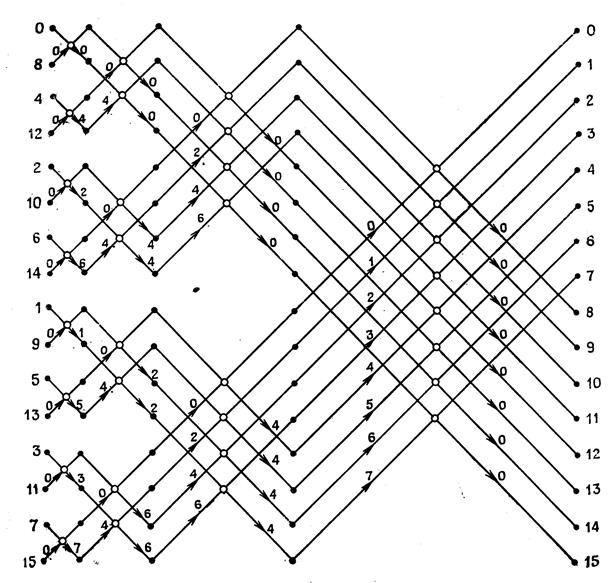
Рис.1. 16-точкове швидке перетворення Фур’є комплексної послідовності за оновою два з двійко-інверсним порядком відліків на вході і прямим порядком відліків на виході
Рис.1. 16-точкове швидке перетворення Фур’є комплексної послідовності за оновою два з прямим порядком відліків на вході і двійко-інверсним порядком відліків на виходіі
Обчислення за даними алгоритмами вимагає виконання m=log2 N етапів, кожен з яких має N/2 базових операцій (БО). Графи БО алгоритмів ШПФк2t і ШПФк2f наведені відповідно на рис.4.1а і 4.1б.
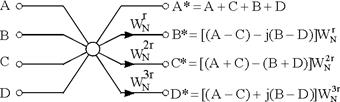
Рис.4.1 Базові операції алгоритмів ШПФк за основою два: а) з часовим прорідженням; б) з частотним прорідженням
Зауважимо, що в загальному випадку БО складаються з однієї операції множення і двох операцій додавання комплексних чисел, тобто вимагається чотири множення і шість додавань дійсних чисел. Алгоритми ШПФ комплексної послідовності за основою чотири. З точки зору кількості необхідних операцій ефективнішими є алгоритми ШПФк за основою чотири (ШПФк4), коли N - точкове ДПФ одразу за один етап розбивається на чотири N/4 - точкові.
Нехай N=4m, m=1,2,..., тоді загальна ФР алгоритму ШПФк4 з часовим прорідженням (ШПФк4t) задається виразом
На основі ФР (4.1) будуємо обчислювальну процедуру
де k=0,1,...,N/4-1; Рекурсивно продовжуючи за формулою (4.1) і процедурою (4.2) розбиття меншої розмірності до чотири-точкових, синтезуємо алгоритм ШПФк4t. Граф БО алгоритму ШПФк4t показаний на рис.4.2.
Рис.4.2 Базова операція алгоритму ШПФк4t
Як і в алгоритмі за основою два, для одержання алгоритму ШПФк4 з частотним прорідженням (ШПФк4f) достатньо розглянути граф ШПФк4t у зворотному напрямку. Граф БО алгоритму ШПФк4f показаний на рис.4.3.
Рис.4.3 Базова операція алгоритму ШПФк4f
Алгоритми ШПФк4 дозволяють на 25% скоротити обчислювальні затрати порівняно з алгоритмами ШПФк2 [4]. Подібним чином будуються алгоритми за основою 8, 16, а також алгоритми за змішаною основою 2-4, 2-4-8 і т.д. У загальному випадку збільшення основи алгоритму веде до зменшення обчислювальних витрат, але при цьому ускладнюється реалізація алгоритму. Алгоритми ШПФ комплексної послідовності за розщепленою основою два-чотири. Важливим етапом в теорії швидких алгоритмів є розробка алгоритму ШПФк за розщепленою основою два-чотири (ШПФк2-4). В них ФР одержується комбінацією ФР алгоритмів ШПФк2 та ШПФк4 [4]. Так для алгоритму ЩПФк2-4 з часовим прорідженням (ШПФк2-4t), ФР має вигляд
де X(k)=ДПФN {x(n)}; Xp(k)=ДПФN/4 {x(4n+p)}, p=1,3; X0(k)=ДПФN/2 {x(2n+1)}. За формулою (4.3) N - точкове ДПФ розбивається на одне N/2- точкове і два N/4- точкові перетворення. На основі (4.3) використовуючи періодичність фазових множників WNr та перетворень Xp(k) будується обчислювальна процедура
Рекурсивно використовуючи ФР (4.3) та процедуру (4.4) до перетворень меншої розмірності, синтезуємо алгоритм ШПФк2-4t. Граф БО алгоритму ШПФк2-4t показаний на рис.4.4.
Рис.4.4 Базова операція алгоритму ШПФк2-4t
Для отримання алгоритму ШПФк2-4 з частотним прорідженням (ШПФк2-4f) використовують ФР алгоритмів ШПФк2f і ШПФк4f. ФР для алгоритму ШПФк2-4f має вигляд
де x0(n)=x(n)+X(n+N/2); an=x(n)-x(n+N/2), n=0,1,...,N/2-1; x1(n)=(an -jan+N/4), x3(n)=(an+jan+N/4)
Процедура переходу до перетворень меншої розмірності наступна:
Шляхом рекурсивного продовження на основі ФР (4.5) та процедури (4.6) розбиття перетворень меншої розмірності синтезується алгоритм ШПФк2-4f. Граф БО такого алгоритму наведений на рис.4.5.
Рис.4.5 Базова операція алгоритму ШПФк2-4f
Алгоритми ШПФк2-4 вдало поєднують простоту структури алгоритмів за основою два з ефективністю алгоритмів з високою основою. Зберігаючи в основному структуру алгоритмів ШПФк2, вони мають найменші обчислювальні затрати серед розглянутого класу алгоритмів. Алгоритми ШПФк Рейдера-Бреннера. Суттєвий недолік вищерозглянутих алгоритмів ШПФк полягає у використанні комплексних фазових множників
де X(n=ДПФN /2{x(2n)},D(k)=ДПФN /2{d(n)}, елементи d(n) число Q відповідно обчислюються за виразами
d(n+1)=x(2n+1)-d(n)-(-1)nQ, n=1,2,…,N/2-1
Необхідно зауважити, що число Q вибирається з умови забезпечення періодичності послідовностей d(n) і b(n).
|
|||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 336; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.190.167 (0.012 с.) |



 (4.1)
(4.1) (4.2)
(4.2)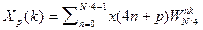 , p=0,1,2,3.
, p=0,1,2,3.
 (4.3)
(4.3) (4.4)
(4.4)
 (4.5)
(4.5)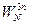 , n=0,1,...,N/4-1.
, n=0,1,...,N/4-1. (4.6)
(4.6)
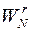 . Алгоритми ШПФк Рейдера-Бреннера (ШПФкРБ) позбавлені цього недоліку, вони використовують фазові множники, що мають структуру дійсних чисел [4]. ФР для алгоритмів ШПФкРБ з косинусними (ШПФкРБс) фазовими множниками записуються наступним чином
. Алгоритми ШПФк Рейдера-Бреннера (ШПФкРБ) позбавлені цього недоліку, вони використовують фазові множники, що мають структуру дійсних чисел [4]. ФР для алгоритмів ШПФкРБ з косинусними (ШПФкРБс) фазовими множниками записуються наступним чином