
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Проверка гипотез о законе распределения
В большинстве случаев закон распределения изучаемой случайной величины Х неизвестен, но существуют основания предполагать, что он имеет вполне определенный вид: нормальный, экспоненциальный или какой-либо другой. В качестве статистического критерия проверки гипотезы о предполагаемом законе неизвестного распределения используют критерий согласия, который используют для проверки согласия предполагаемого вида распределения с опытными данными на основе исследуемой выборки. В статистике используют различные критерии согласия: Пирсона, Колмогорова, Фишера и др. Критерий Пирсона
Наиболее часто при проверке гипотезы о предполагаемом законе неизвестного распределения пользуются критерием Пирсона. Пусть задана выборка из генеральной совокупности Необходимо проверить нулевую гипотезу
Правило проверки: 1. Вычисляют 2. Находят теоретические частоты Вычислить теоретические частоты
где
- функция Гаусса, значение которой в точке
- вероятность попадания значений случайной величины Для определения
Таблица 1.8
3. Сравнивают эмпирические ( 1) составляется расчетная табл.1.9, из которой определяется наблюдаемое значение критерия
Таблица 1.9
2) Определяется число степеней свободы
где
Для нормального распределения число степеней свободы равно 4. По данным таблицы критических точек (квантилей) распределение
Когда В случае если Замечание: 1) Объем изучаемой выборки должен быть достаточно большой 2) Малочисленные частоты при В случае, когда производилось объединение частот при определении числа степеней свободы по формуле
Критерий Колмогорова
На практике кроме критерия
называемой статистикой критерия Колмогорова. Критерий Колмогорова в своем классическом виде является более мощным, чем критерий Пирсона и может быть использован для проверки гипотезы о соответствии эмпирического распределения любому теоретическому непрерывному распределению Доказано, что какой бы ни была функция распределения
Задавая уровень значимости
можно определить соответствующее критическое значение При этом график функции K (l) имеет следующий вид:
Значения K (l) находят, пользуясь данными табл. 1.10. Таблица 1.10
Если найденному значению Если вероятность Схема применения критерия Колмогорова следующая: 1. Строят эмпирическую функцию распределения 2. Определяют меру расхождения между теоретическим и эмпирическим распределениями
где n – объем выборки.
3. Если вычисленное значение Замечание: Можно отметить, что решение подобных задач можно было бы найти с помощью критерия
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 411; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.162.247 (0.021 с.) |
 в виде статистического интервального ряда.
в виде статистического интервального ряда. о том, что генеральная совокупность
о том, что генеральная совокупность  и
и  (формулы 1.10-1.12, 1.16).
(формулы 1.10-1.12, 1.16).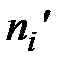 .
. , (1.45)
, (1.45) – объем выборки,
– объем выборки, – шаг,
– шаг, ; (1.46)
; (1.46) (1.47)
(1.47) , находится по таблице (приложение 3).
, находится по таблице (приложение 3). (1.48)
(1.48) -й интервал.
-й интервал.











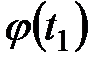

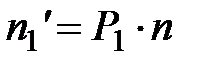













 ) и теоретические (
) и теоретические ( по формуле:
по формуле: . (1.49)
. (1.49)





















 на основании формулы:
на основании формулы: , (1.50)
, (1.50) – число интервалов;
– число интервалов; – число параметров предполагаемого распределения.
– число параметров предполагаемого распределения. в виду того, что
в виду того, что  - нормальный закон распределения характеризуется двумя параметрами
- нормальный закон распределения характеризуется двумя параметрами  и
и 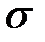 .
.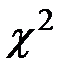 (приложение 4) по заданному уровню значимости
(приложение 4) по заданному уровню значимости  и числу степеней свободы определяют
и числу степеней свободы определяют  правосторонней критической области.
правосторонней критической области. то отвергнуть гипотезу
то отвергнуть гипотезу 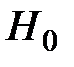 о нормальном распределении генеральной совокупности оснований не существует.
о нормальном распределении генеральной совокупности оснований не существует. – гипотеза отвергается.
– гипотеза отвергается. .
. следует объединять, в том числе и соответствующие им теоретические частоты.
следует объединять, в том числе и соответствующие им теоретические частоты.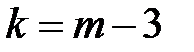 в качестве
в качестве  необходимо принимать число интервалов, оставшихся после объединения частот.
необходимо принимать число интервалов, оставшихся после объединения частот. часто используют критерий Колмогорова, в котором в качестве меры расхождения между теоретическим и эмпирическим распределениями рассматривается максимальное значение абсолютной величины разности между эмпирической функцией распределения
часто используют критерий Колмогорова, в котором в качестве меры расхождения между теоретическим и эмпирическим распределениями рассматривается максимальное значение абсолютной величины разности между эмпирической функцией распределения  и соответствующей ей теоретической функцией распределения:
и соответствующей ей теоретической функцией распределения: , (1.51)
, (1.51) с заранее известными параметрами.
с заранее известными параметрами. непрерывной случайной величины
непрерывной случайной величины  , при неограниченном увеличении числа наблюдений
, при неограниченном увеличении числа наблюдений  вероятность неравенства
вероятность неравенства  стремится к пределу:
стремится к пределу: . (1.52)
. (1.52) , из соотношения (1.53):
, из соотношения (1.53): , (1.53)
, (1.53) .
.
 соответствует очень малая вероятность, то есть
соответствует очень малая вероятность, то есть  , то расхождение между эмпирическим и теоретическим распределениями нельзя считать случайным. Следовательно, рассматриваемая выборка не подчиняется нормальному закону распределения.
, то расхождение между эмпирическим и теоретическим распределениями нельзя считать случайным. Следовательно, рассматриваемая выборка не подчиняется нормальному закону распределения. , то расхождение между частотами может быть случайным, и распределения хорошо соответствуют одно другому.
, то расхождение между частотами может быть случайным, и распределения хорошо соответствуют одно другому.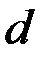 с использованием формулы (1.54) и вычисляют величину
с использованием формулы (1.54) и вычисляют величину  :
: . (1.54)
. (1.54) – максимум абсолютного значения разности между накопленными эмпирическими частотами М и накопленными теоретическими частотами
– максимум абсолютного значения разности между накопленными эмпирическими частотами М и накопленными теоретическими частотами 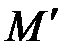 ,
, , то нулевая гипотеза
, то нулевая гипотеза  о том, что случайная величина
о том, что случайная величина  , то считают, что гипотеза
, то считают, что гипотеза  . Потенциальное преимущества критерия Колмогорова в том, что он не требует группирования данных (с неизбежной потерей информации), а дает возможность рассматривать индивидуальные наблюдаемые значения. Этот критерий можно успешно применять для малых выборок. Считается, что его мощность выше, чем у критерия
. Потенциальное преимущества критерия Колмогорова в том, что он не требует группирования данных (с неизбежной потерей информации), а дает возможность рассматривать индивидуальные наблюдаемые значения. Этот критерий можно успешно применять для малых выборок. Считается, что его мощность выше, чем у критерия 


