
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Імовірність випадкової подіїСтр 1 из 21Следующая ⇒
Змістовий модуль 1 ІМОВІРНІСТЬ ВИПАДКОВОЇ ПОДІЇ
Тема1. Основні поняття теорії ймовірностей
Теорія ймовірностей - математична наука, що вивчає закономірності у випадкових явищах. Випадковим називається таке явище, яке при багаторазовому повторенні досліду протікає щораз по-іншому. Наприклад, вимірювання - якщо ми бажаємо отримати точний результат, стрілянина по мішені являє класичний приклад випадкового явища, погодні умови і т. інше. На відміну від випадкових явищ існують детерміновані явища. Це, як правило, закони природи, які вивчаються в курсі фізики, наприклад: - прискорення вільного падіння дорівнює 9,8 м/с2; - сила, прикладена до матеріальної точки, надає їй прискорення (за формулою F=ma); - струм, що протікає через опір R під дією напруги U, пропорційний напрузі I=U/R. Таким чином, якщо при відтворенні певних умов незмінно відбувається певна подія (та сама, тобто результат незмінно повторюється), то має місце детерміноване явище. Прогноз результату такого досліду можна здійснити, не проводячи експерименту. У випадку, коли на результат досліду впливає ряд факторів, урахувати які неможливо або дуже складно (крім того, ці фактори можуть змінюватися випадковим образом), скласти математичну модель, що прогнозує розвиток такого явища в детерміністському поданні неможливо. У такому випадку намагаються знайти у випадкових явищах ті або інші закономірності. Такі закономірності виявляються при масовому повторенні дослідів. Якщо їх удається знайти, то випадкове явище є статистично однорідним. Якщо закономірності в явищі відсутні, тобто виявити їх не удається, то таке явище є невизначеним і вимагає додаткового дослідження. Одним з основних у теорії ймовірностей є поняття випадкової події. Випадкова подія - це всякий факт, що в результаті досліду може відбутися або не відбутися. Випадкові події позначають великими буквами латинського алфавіту: A={влучення в мішень}, B={прибуття трамвая на зупинку}, C={поломка технічного устрою}, D={коротке замикання в мережі}. Дослідом називається відтворена сукупність умов, у яких може відбутися випадкова подія. Імовірність випадкової події – це числова міра ступеню об'єктивної можливості появи даної події в результаті досліду. Імовірність події А позначається Р(А).
За одиницю виміру ймовірності приймають імовірність достовірної події Е, тобто такої, яка в результаті досліду обов'язково відбудеться: Р(Е) = 1. Протилежна достовірному подія називається неможливою і позначається `Е. Імовірність неможливої події: Р(`Е) = 0. Відповідно ймовірність будь-якої випадкової події А укладена між нулем і одиницею: 0 £ Р(А) £ 1.
Класичний і статистичний методи визначення Тема 2. Операції над подіями. Теореми теорії ймовірностей. Теорема додавання Імовірність суми двох несумісних подій А і В дорівнює сумі ймовірностей цих подій, тобто Р(А + В) = Р(А) + Р(В) (2.1) Доведемо це. Нехай дослід має n можливих наслідків, в числі яких m сприяють появі події А і k - появі події В.
Оскільки подія С перебуває в появі події А, якої сприяє m наслідків досліду або події В, якої сприяє k наслідків, то події С сприяють m+k наслідків досліду. Тоді імовірність події С за класичною формулою визначиться в такий спосіб:
Слідства теореми додавання: За методом математичної індукції (узагальнення) теорему додавання ймовірностей можна розповсюдити на будь-яке кінцеве число несумісних подій: С = SАi P(SАi) = SP(Аi). Слідство 1. Якщо події А1, А2, …, Аi, …, Аn утворюють повну групу несумісних подій, то сума їхніх імовірностей дорівнює 1: P(SАi) = SP(Аi) = 1. (2.2) Слідство 2. Сума ймовірностей двох протилежних подій дорівнює одиниці: P(A) + P((A) = 1, звідки імовірність будь-якої випадкової події: P(A) = 1 - P((A). У випадку, коли дві події є сумісними, імовірність їхньої суми дорівнює сумі ймовірностей цих подій мінус імовірність їхньої спільної появи: Р(А + В) = Р(А) + Р(В) - Р(А*В) (2.3) Доведемо це. Нехай дослід має n можливих наслідків, в числі яких m сприяють появі події А, k - появі події В і l - появі події АВ.
Оскільки подія С перебуває в появі події А, якої сприяє m наслідків досліду або події В, якої сприяє k наслідків, то події С сприяють m+k-l наслідків досліду. Тоді імовірність події С за класичною формулою визначиться в такий спосіб:
Теорема множення Імовірність добутку двох подій А і В дорівнює добутку ймовірності одного з них на умовну ймовірність іншого, обчислену за умови, що перша відбулася:
Р(А * В) = Р(А) * Р(В|А). (2.4) Доведемо це. Нехай дослід має n можливих наслідків, в числі яких m сприяють появі події А, k - появі події В і l - появі події АВ.
Події АВ, сприяють l наслідків досліду:
Тоді імовірність події АВ визначиться в такий спосіб:
Якщо події А і В незалежні, то умовна ймовірність події В дорівнює безумовній імовірності цієї події, Р(В|А) = Р(В). Слідство. Імовірність добутку двох незалежних подій дорівнює добутку ймовірностей цих подій: Р(А * В) = Р(А) * Р(В) (2.5) Якщо маємо кілька незалежних подій:
Формула повної ймовірності Формула повної ймовірності є слідством двох теорем теорії ймовірностей. Нехай передбачається проведення досліду, про умови протікання якого можна зробити N взаємовиключних припущень (гіпотез). Умови протікання досліду (гіпотези) являють собою повну групу неспільних подій Н1, Н2,…, НN, імовірності яких Р(Нi) відомі. Деяка випадкова подія А може з'явитися при будь-яких умовах протікання досліду з різною ймовірністю. Уявимо подію А як суму несумісних подій: А=Н1А+Н2А+…+НNА. Застосовуючи теореми додавання й множення, дістанемо:
Таким чином, повна безумовна ймовірність події А з урахуванням випадковості умов протікання досліду дорівнює сумі добутків ймовірностей кожної з гіпотез на умовну ймовірність події А при кожній з гіпотез.
Формула Бернуллі На практиці доводиться зіштовхуватися з такими задачами, які можна представити у вигляді багаторазово повторюваних незалежних випробувань. Якщо імовірність появи події А в одному досліді та сама, то імовірність m появ події А в n дослідах можна визначити за формулою Бернуллі
де
р - імовірність появи події А в одному досліді; q = 1 - p - імовірність не появи події А в одному досліді. Користуючись формулою Бернуллі, можна дістати найімовірніше число появ події А. Найімовірнішим числом появи події А в n незалежних дослідах називається таке число, для якого імовірність перевищує або, принаймні, не менше ймовірності кожного з інших можливих чисел появи події А. Для визначення найімовірнішого числа користуються формулою: np – q £ m0 £ np + p (2.9) причому, m0 — може бути тільки цілим числом. Якщо np - ціле число, то m0=np. Локальна теорема Лапласа Локальна теорема Лапласа дає асимптотичну формулу, що дозволяє приблизно знайти імовірність появи подій рівно m разів в n дослідах, якщо число випробувань досить велике. Якщо імовірність р появи події А в кожному випробуванні постійна й відмінна від нуля й одиниці, то імовірність Pn(m) того, що подія А з'явиться в n дослідах рівно m разів, приблизно дорівнює, і тим точніше, чим більше n, значенню функції
де
Інтегральна теорема Лапласа Якщо в повторних незалежних випробуваннях, у кожному з яких імовірність появи події А постійна й дорівнює р, необхідно обчислити ймовірність того, що подія А з'явиться в n випробуваннях не менше m1 і не більше m2 разів, це можна зробити за допомогою інтегральної теореми Лапласа.
Якщо імовірність р настання події А в кожному випробуванні постійна й відмінна від нуля й одиниці, то приблизно імовірність Pn(m1,m2), того, що подія А з'явиться у випробуваннях від m1 до m2 разів,
де При розв'язанні задач користуються спеціальними таблицями, тому що невизначений інтеграл (2.11) не виражається через елементарні функції. У довідкових таблицях приводяться значення інтеграла Таким чином, приблизно імовірність того, що подія А з'явиться в n незалежних дослідах від m1 до m2 разів. Pn(m1,m2) = Ф(х")-Ф(х'), (2.12)
Формула Пуассона Якщо імовірність р настання події в окремому випробуванні близька до нуля, то навіть при великій кількості випробувань n, але при невеликому значенні добутку np одержувані за формулою Лапласа значення ймовірностей Рn(m) виявляються недостатньо точними й виникає потреба в іншій наближеній формулі. Якщо імовірність р настання події А в кожному випробуванні постійна, але мала, число незалежних випробувань n досить велике, але значення добутку np залишається невеликим (не більше десяти), то імовірність того, що в цих випробуваннях подія А наступить m разів, можна визначити за формулою Пуассона:
Змістовий модуль 2 Рис. 3.1 – Графічна інтерпретація ряду розподілу.
Найбільш загальною формою закону розподілу для всіх випадкових величин є функція розподілу.
Функція розподілу Для характеристики як безперервних так і дискретних випадкових величин зручніше користуватися не ймовірністю події X=xi (тому що значень xi може бути багато), а ймовірністю події X < x. Функція розподілу випадкової величини Х дорівнює імовірності того, що випадкова величина Х прийме значення, менше x: F(х) = P{X < x} (3.1) Геометрично функція розподілу – це імовірність того, що значення випадкової величини потрапить лівіше хi.
Рис. 3.2 – Розташування значень X < x Функція розподілу дискретної випадкової величини являє собою розривну, східчасту функцію, що має перегони в точках, що відповідають можливим значеннямх1, х2, …, хnвипадкової величини Х, які дорівнюють ймовірностямр1, р2, …, рnцих значень. У випадку безперервної випадкової величини функція розподілу звичайно має вигляд плавної кривої.
Щільність розподілу
Нехай є безперервна випадкова величина Х з функцією розподілу F(х).
Рис. 3.3 - Функція розподілу безперервної випадкової величини
Говорити про розподіл ймовірностей між значеннями безперервної випадкової величини нема рації, тому що число її значень нескінченно навіть на невеликому інтервалі, й імовірність того, що безперервна випадкова величина прийме одне-єдине своє значення xi дорівнює нулю. Тому, характеризуючи безперервну випадкову величину, завжди говорять про влучення її значень у той чи інший інтервал. З рисунка 3.3 видно, що імовірність влучення Х в інтервал Dх1 більше, ніж в інтервал Dх2, оскільки приріст функції розподілу DF(х1) > DF(х2). З математики відомо, що Таким чином, закон розподілу ймовірностей безперервних випадкових величин зручніше визначати завданням не функції розподілу F(х), а щільності розподілу ймовірностей f(х), що являє собою похідну від F(х) по х:
Передбачається, що F(x) безперервна й диференційована. Щільністю розподілу випадкової величини Х у точці х називається похідна функції розподілу Х у цій точці. На графіку щільності розподілу ймовірність представляється площею.
Рис. 3.4 – Графік щільності розподілу
Властивості щільності розподілу ймовірностей: 1. Щільність розподілу невід’ємна, тобто f(x) ³ 0 як похідна неубутної функції. 2. Інтеграл від щільності розподілу в нескінченних межах дорівнює одиниці
3. Імовірність влучення безперервної випадкової величини в інтервал (х1, х2)
4. Функція розподілу визначається співвідношенням:
Функцію розподілу F(x) іноді називають інтегральним законом розподілу, а щільність розподілу f(x) - диференціальним законом розподілу. Випадкових величин
Закон розподілу Пуассона Можна показати, що при n ® ¥ границя вираження біноміального розподілу дорівнює
Отримана формула виражає закон розподілу Пуассона. Таким чином, коли імовірність p появи події А в кожному окремому досліді мала, а число дослідів n велике, біноміальний закон розподілу дискретної випадкової величини може бути приблизно замінений законом Пуассона:
Закон розподілу Пуассона визначається одним параметром а = np, що є одночасно математичним сподіванням і дисперсією випадкової величини Х, розподіленої за законом Пуассона. Розподіл Пуассона з параметром а = np можна приблизно застосовувати замість біноміального, коли число дослідів n дуже велике, а імовірність p дуже мала, тобто в кожному окремому досліді подія А з'являється вкрай рідко. Розподіл Пуассона часто використовується, коли ми маємо справу із числом подій, що з'являються на проміжку часу. Наприклад, число дефектів на новій дільниці шосе довжиною 10 км, число місць витоку води на 100 км водопроводу, число поломок надійного технічного устрою за певний період часу, наприклад, за рік.
Закон рівномірної щільності Безперервна випадкова величина Х має рівномірний розподіл на дільниці від a до b, якщо її щільність розподілу на цій дільниці постійна:
Наприклад, помилка Х при грубому вимірюванні, яка може приймати з постійною щільністю імовірності будь-яке значення між двома сусідніми цілими діленнями. Грубий вимір відрізняється від точного в тім, що результат грубих вимірів при повторенні завжди той самий; при точному ж вимірі - результат від разу до разу змінюється. Іншим прикладом рівномірного розподілу є абсциса навмання поставленої точки на відрізку [a, b]. Визначимо числові характеристики випадкової величини, розподіленої рівномірно.
Математичне сподівання:
Дисперсія:
Середнє квадратичне відхилення:
Визначимо ймовірність влучення значень рівномірно розподіленої випадкової величини на інтервал (a, b):
Функція рівномірного розподілу:
Характеристики системи Функції випадкових величин Функції однієї або декількох випадкових величин доводиться розглядати, коли аргументом деякої функції Y є система випадкових величин (X1, X2,…, Xn), закон розподілу яких відомий. Функція Y є випадковою величиною, закон розподілу якої варто визначити. У більшості задач для визначення числових характеристик функції декількох випадкових величин досить знати тільки числові характеристики аргументів. 1. Математичне сподівання суми двох залежних або незалежних випадкових величин X і Y дорівнює сумі їхніх математичних сподівань: M[X+Y] = S(xi+yi)pi = Sxipi +Syipi = M[X] + M[Y]. (6.10) Методом математичної індукції (узагальнення) дістанемо: M[SXi] = SM[Xi], Математичне сподівання суми n випадкових величин дорівнює сумі їхніх математичних сподівань. 2. Математичне сподівання добутку двох випадкових величин X і Y дорівнює добутку їхніх математичних сподівань плюс кореляційний момент. Запишемо вираження для кореляційного моменту:
звідки дістанемо M[XY] = M[X] * M[Y] + Kxy.(6.11) Якщо випадкові величини X і Y незалежні, математичне сподівання добутку дорівнює добутку їхніх математичних сподівань. 3. Дисперсія суми двох випадкових величин X і Y дорівнює сумі дисперсій цих величин плюс подвоєний кореляційний момент: D[X+Y] = M[((X+Y)-M(X+Y))2] = =M[X2+2XY+Y2 -2(X+Y)M(X+Y)+M 2(X+Y)] = = M[X2+2XY+Y2]-2M(X+Y)M(X+Y)+M 2(X+Y) = = M[X2+2XY+Y2]-(M[X]+ M[Y])2 = =M[X2]+ M[Y2]-M 2[X]- 2M[X]*M[Y]- M 2[Y] = =D[X] + D[Y]+2M[XY] – 2M[X]M[Y] = D[X] + D[Y]+2Kxy Таким чином, дисперсія суми двох випадкових величин X і Y дорівнює сумі їхніх дисперсій плюс подвоєний кореляційний момент D[X+Y] = D[X] + D[Y] + 2Kxy,(6.12) Якщо X і Y - незалежні випадкові величини, то дисперсія їхньої суми дорівнює сумі їхніх дисперсій, тоді сума n незалежних випадкових величин: D[SXi] = SD[Xi], звідки середнє квадратичне відхилення суми:
4. Дисперсія добутку двох незалежних випадкових величин X і Y визначається за формулою D[XY] = D[X]*D[Y] + M[X]2D[Y] + M[Y]2D[X](6.13)
Тема 7. Закон великих чисел Великих чисел Якщо подія має дуже малу ймовірність (відмінну від нуля), то в одиничному випробуванні ця подія може наступити й не наступити. Але так міркуємо ми тільки теоретично, а на практиці вважаємо, що подія, яка має малу імовірність, не наступить, і тому нехтуємо нею. Однак, у рамках математичної теорії не можна відповісти на запитання, якою повинна бути верхня границя імовірності, щоб можна було назвати «практично неможливими» події, імовірності яких не будуть перевищувати знайденої верхньої границі. Нехай, наприклад, робітник виготовляє на верстаті 100 виробів, з яких один в середньому виявляється бракованим. Очевидно, що імовірність браку дорівнює 0,01, але нею можна зневажити й вважати робітника непоганим фахівцем. Але якщо будівельники будуть будувати будинки так, що з 100 будинків (у середньому) в одному будинку буде мати місце руйнування даху, то навряд чи можна зневажити імовірністю такої події. Таким чином, у кожному окремому випадку варто виходити з того, наскільки важливі наслідки в результаті настання події. Імовірність, якою можна зневажити в даному дослідженні, називається рівнем значимості. Сформулюємо принцип практичної впевненості: «Якщо випадкова подія має малу ймовірність (наприклад, р < 0,01), то при одиничному випробуванні можна практично вважати, що ця подія не відбудеться, а якщо подія має ймовірність, близьку до одиниці (р > 0,99), то практично при одиничному випробуванні можна вважати, що ця подія відбудеться напевно». Основною закономірністю масових випадкових явищ є властивість усталеності середніх результатів. У широкому значенні слова під «законом великих чисел» розуміють відому із глибокої стародавності властивість усталеності масових випадкових явищ, що полягає в тому, що середній результат великої кількості випадкових явищ практично перестає бути випадковим і може бути передвіщений з достатньою визначеністю. У вузькому значенні слова під «законом великих чисел» розуміють сукупність теорем, у яких встановлюється факт наближення середніх характеристик явища до деяких постійних величин у результаті великої кількості спостережень. Розглянемо деякі з них. 1. Лема Маркова. Якщо випадкова величина X не приймає від’ємних значень, то для будь-якого позитивного числа справедлива нерівність:
Доказ. 1) Нехай X — дискретна випадкова величина, задана рядом розподілу, причому 0 £ х1 < х2 <…<хn.
Всі значення випадкової величини розіб'ємо на дві групи. До першої групи віднесемо значення, менші a (нехай це будуть х1, x2,..., хk), до другої - всі інші значення більші або рівні a (xk+1, хk+2,..., хn). Як відомо, математичне сподівання дискретної випадкової величини визначається за формулою: M[X]=x1p1 + x2p2 +... + xkpk + xk+lpk+l +... + хnрn. Відкинемо в правій частині формули перші k доданків. Оскільки рi > 0, хi- ³0 і, крім того, при хi ³ a, i ³ k+l, буде мати місце наступна нерівність: M[X] ³ xk+lpk+l +... + хnрn. ³ a(pk+l +... + рn). З того, що pk+l +... + рn = P{X=xk+1}+…+P{X=xn}=P{X³a}, слідкує, що: M[X] ³ a P{X³ a}. Розділимо обидві частини останньої нерівності на a і дістанемо нерівність (7.1). 2) Нехай X - безперервна випадкова величина. Оскільки за умовою X не приймає невід'ємних значень, то її щільність імовірності f(х) = 0 при всіх х < 0. Тому
розділимо на ³ a, дістанемо нерівність (7.1). Лему доведено.
2. Нерівність Чебишева. Імовірність того, що відхилення випадкової величини Х від її математичного сподівання за абсолютною величиною буде менше деякого додатного числа e, обмежена знизу величиною
Доказ. Нехай маємо випадкову величину (Х-M[X])2. Оскільки вона приймає тільки додатні значення, до неї можна вжити лему Маркова, покладаючи в ній a=e2, дістанемо:
Зазначимо, що
3. Теорема Чебишева. При необмеженому збільшенні числа n незалежних випробувань середня арифметична спостережуваних значень випадкової величини сходиться за імовірністю до її математичного сподівання, тобто для любого додатного e
Ця теорема встановлює зв'язок між середньою арифметичною Доказ. Спостережувані значення Х (х1, х2,…,хn) у силу незалежності дослідів можна розглядати як незалежні випадкові величини, що мають однаковий розподіл (таке ж, як в X) з однаковими параметрами – математичним сподіванням а = М[Х] і дисперсією D[X]. За властивостями математичного сподівання й дисперсії можна записати:
Скористаємося нерівністю Чебишева для випадкової величини Х і підставимо в нього отримані параметри:
Якщо тепер в отриманій нерівності взяти як завгодно мале додатне e і необмежено збільшити n, дістанемо
що й доводить теорему Чебишева. З теореми Чебишева випливає важливий практичний висновок: невідоме значення математичного сподівання випадкової величини ми вправі замінити середнім арифметичним значенням, отриманим за досить великою кількістю дослідів. При цьому, чим більше проведено дослідів, тим з більшою ймовірністю можна чекати, що пов'язана із цією заміною помилка ( 4. Теорема Бернуллі. При необмеженому зростанні числа незалежних випробувань n відносна частота
За допомогою цієї теореми встановлюється зв'язок між відносною частотою події і її ймовірністю. Вона була доведена Я. Бернуллі (опублікована в 1713р.) і поклала початок теорії ймовірностей як науки. Доказ. Відносна частота
Запишемо нерівність Чебишева для випадкової величини
Остаточно дістанемо:
Як би малим не було число e, при n®¥ величина дробі З теореми Бернуллі витікає, що при досить великій кількості випробувань відносна частота Незважаючи на те, що при необмеженому зростанні числа незалежних випробувань різниця Таким чином, при необмеженому числі незалежних випробувань може статися, що Змістовий модуль 3 Статистичними даними Однією із задач математичної статистики є одержання оцінок числових характеристик випадкових величин. Іншою задачею є визначення закону розподілу випадкової величини за статистичним даними. Оскільки ці дані завжди обмежені, то виникає задача згладжування або вирівнювання статистичних рядів за допомогою аналітичних виразів, що є найбільш компактним вираженням закономірності. Статистичний (варіаційний) ряд дозволяє побудувати шукані статистичні закони розподілу. Зокрема, для того, щоб знайти статистичну функцію розподілу F*(x), досить підрахувати число варіантів, у яких ознака Х прийняла значення менші х, тобто X<x. Якщо число таких варіантів m(x), а обсяг сукупності дорівнює n, то
Якщо результати спостереження зведені в згрупований статистичний ряд, то на його підставі будують гістограму, з урахуванням того, що частота появ ознаки на i-м інтервалі буде
де mi – кількість появ х на i-м інтервалі. Для оформлення статистичного ряду у вигляді гістограми по осі абсцис відкладають інтервали ряду, а потім на кожному інтервалі будують прямокутник, площа якого дорівнює р*i. Задача вирівнювання статистичних рядів зводиться до підбору теоретичної кривої розподілу, що виражає лише істотні риси статистичного матеріалу. Якщо клас функцій, що описують розподіл, відомий, то задача зводиться до раціонального вибору параметрів розподілу.
Наприклад, гістограма, наведена на рис. 8.3, наводить на думку про нормальний розподіл ознаки Х:
Тоді задача зводиться до відшукання двох параметрів - вибіркової середньої `х і вибіркового середнього квадратичного відхилення s. Одним з методів рішення поставленої задачі є метод моментів (початкових і центральних), що був запропонований в 1894 році англійцем Пірсоном. Відповідно до цього методу числові параметри розподілу вибираються з таким розрахунком, щоб кілька найважливіших числових характеристик (моментів) були рівні їхнім статистичним оцінкам. Зокрема, математичне сподівання й дисперсія приймаються рівними їхнім статистичним оцінкам - вибіркової середньої й вибіркової дисперсії: mx = Іншим методом визначення статистичних оцінок параметрів розподілу є метод максимальної правдоподібності, запропонований в 1912 році англійцем Фішером. Метод найменших квадратів Для визначення значень параметрів ryx і b рівняння регресії (10.3) застосовується метод найменших квадратів (МНК), що дозволяє при відомому класі залежності `yx = j(x) так вибрати їхні значення, щоб вона щонайкраще відображала дані спостережень. При використанні МНК вимога найкращого узгодження `yx = j(х) з дослідними даними зводиться до того, щоб сума квадратів відхилень кривої, що згладжує залежність, від експериментальних точок оберталася в мінімум:
де yi – значення Y, отримані в результаті спостережень; yiр - розрахункові значення Y, отримані за вираженням кривої, що згладжує j (х). Якщо всі виміри провадилися з однаковою точністю й помилки вимірів розподілені за нормальним законом, то знайдена залежність буде найбільш ймовірною із всіх можливих у даному класі функцій. З огляду на те, що yiр = j(хi), вираження (9.4) можна записати у вигляді
Невідомі параметри шуканої залежності визначають, записавши її не тільки як функцію аргументу х, але і як функцію невідомих параметрів aj.
Умова (10.6) виконується, якщо всі часткові похідні суми квадратів відхилень за параметрами aj будуть дорівнювати нулю. Часткові похідні дають систему m+1 рівнянь із m+1 невідомими, розв'язання якої дає шукані параметри aj, що задовольняють умові (10.5). Дістанемо для лінійного рівняння регресії (10.3) методом найменших квадратів вираження для коефіцієнта регресії rух і вільного члена b. Для цього підставимо в (10.6) вираження (10.3)
Для відшукання мінімуму візьмемо похідні за параметрами rух і b і дорівняємо їх до нуля, дістанемо систему рівнянь:
з якої в результаті перетворень отримаємо:
звідки виразимо rух і b
Статистичні гіпотези Будь-яка інформація, отримана в результаті обробки статистичних даних, носить імовірнісний характер. Зокрема, оцінка генеральної середньої є величиною випадковою, розподіленою нормально з параметрами `х і Основну гіпотезу, сформульовану в результаті обробки статистичного матеріалу, називають нульовою гіпотезою й позначають Н0. На противагу нульовій гіпотезі призначають одну або декілька альтернативних (конкуруючих) гіпотез. Їх позначають Н1, Н2, … і т.д. Наприклад, якщо перевіряється гіпотеза про рівність параметра а деякому заданому значенню а0, то як альтернативні гіпотези можна розглянути гіпотези, що а більше або менше а0: Н0: а = а0; Н1: а > а0; Н2: а < а0; Н3: а ¹ а0. Вибір альтернативної гіпотези обумовлюється формулюванням задачі. В якості критеріїв для перевірки статистичних гіпотез використовують випадкові величини (статистики), особливість яких полягає в тому, що кожна з них має свій закон розподілу, що не залежить від закону розподілу генеральної сукупності й вибірки, а залежить від умов обробки вибіркових даних. Значення цих випадкових величин, позначимо їх Z, з відповідними їм ймовірностями приводяться в довідкових таблицях.
|
||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 271; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.181.52 (0.225 с.) |

 .
.
 .
. ;
;  ;
;  ;
;  ;
;  .
. .
. .
. . (2.6)
. (2.6) (2.8)
(2.8) - імовірність того, що в n випробуваннях подія А з'явиться рівно m разів;
- імовірність того, що в n випробуваннях подія А з'явиться рівно m разів; - число сполучень із n елементів по m;
- число сполучень із n елементів по m; , (2.10)
, (2.10) , а значення функції
, а значення функції  визначаються з довідкових таблиць. Функція j (х) парна, тобто j (-х) = j (х).
визначаються з довідкових таблиць. Функція j (х) парна, тобто j (-х) = j (х). , (2.11)
, (2.11) ;
; 
 . Функція Ф(х) непарна, тобто Ф(-х) = -Ф(х). Таблиця містить значення функції Ф(х) тільки для х Î [0; 5]; для х > 5 приймають Ф(х) = 0,5.
. Функція Ф(х) непарна, тобто Ф(-х) = -Ф(х). Таблиця містить значення функції Ф(х) тільки для х Î [0; 5]; для х > 5 приймають Ф(х) = 0,5. (2.13)
(2.13)

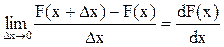
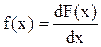 (3.2)
(3.2)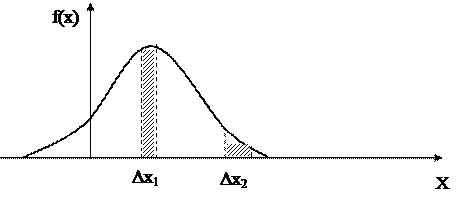
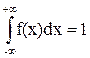
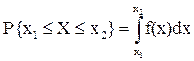 .
.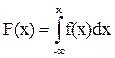 .
. 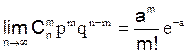 .
.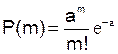 (5.9)
(5.9)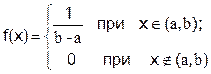 (5.21)
(5.21)
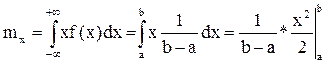
 (5.22)
(5.22) (5.23)
(5.23) (5.24)
(5.24)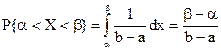 (5.25)
(5.25)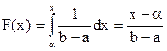 . (5.26)
. (5.26)
 ,
, .
.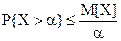 (7.1)
(7.1)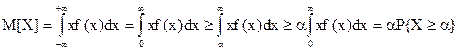 ,
, або
або  . (7.2)
. (7.2) .
. , а також урахуємо, що ймовірність
, а також урахуємо, що ймовірність  дорівнює ймовірності
дорівнює ймовірності  . На цій підставі можемо записати:
. На цій підставі можемо записати: . (7.3)
. (7.3) спостережуваних значень випадкової величини X і її математичним сподіванням М[X].
спостережуваних значень випадкової величини X і її математичним сподіванням М[X].
 .
.
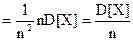 .
. (7.4)
(7.4) ,
, ) не перевершить задану величину e. При відомому значенні дисперсії D[X], наприклад, за заданим значенням імовірності
) не перевершить задану величину e. При відомому значенні дисперсії D[X], наприклад, за заданим значенням імовірності  й максимальній припустимій помилці e, визначити число необхідних дослідів n; або по заданим P і n визначити e; а також, по заданим e і n визначити границю ймовірності події
й максимальній припустимій помилці e, визначити число необхідних дослідів n; або по заданим P і n визначити e; а також, по заданим e і n визначити границю ймовірності події  .
. появи події А сходиться за імовірністю до його ймовірності Р, тобто
появи події А сходиться за імовірністю до його ймовірності Р, тобто , (7.5)
, (7.5) ;
; 
 .
. . (7.6)
. (7.6) ®0, а
®0, а  .
. може виявитися як завгодно малою, все ж таки не можна сказати, що
може виявитися як завгодно малою, все ж таки не можна сказати, що  . Таке твердження було б невірним, тому що в даному питанні не виконуються необхідні умови, що входять до складу визначення поняття границі. Справді, може статися, що подія А буде відбуватися при всіх наступних випробуваннях, починаючи з деякого номера n > N і тоді
. Таке твердження було б невірним, тому що в даному питанні не виконуються необхідні умови, що входять до складу визначення поняття границі. Справді, може статися, що подія А буде відбуватися при всіх наступних випробуваннях, починаючи з деякого номера n > N і тоді  .
. . Отже,
. Отже, 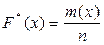 (8.5)
(8.5)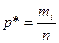 ,
,
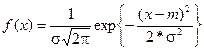 .
. , Dх =
, Dх = 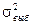 .
.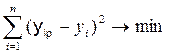 . (10.4)
. (10.4) (10.5)
(10.5)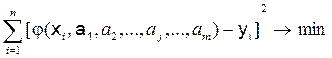 (10.6)
(10.6)
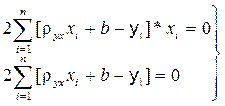 , (10.7)
, (10.7)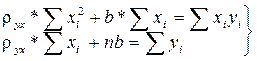 (10.8)
(10.8)
 (10.9)
(10.9) . Оцінка генеральної дисперсії також випадкова. Тому будь-який висновок, заснований на статистичних даних, є науковим припущенням і називається статистичною гіпотезою. Статистичні гіпотези підлягають перевірці, ціль якої - визначити, чи не суперечить висунута гіпотеза вихідному статистичному матеріалу (вибірці).
. Оцінка генеральної дисперсії також випадкова. Тому будь-який висновок, заснований на статистичних даних, є науковим припущенням і називається статистичною гіпотезою. Статистичні гіпотези підлягають перевірці, ціль якої - визначити, чи не суперечить висунута гіпотеза вихідному статистичному матеріалу (вибірці).


