Для решения рассматриваемой задачи используем уравнения движения (1.8), но предварительно их упростим. С учетом малости угловых скоростей  и
и  по сравнению с постоянными угловыми скоростями коррекции
по сравнению с постоянными угловыми скоростями коррекции  и
и  , будем пренебрегать влиянием скоростей
, будем пренебрегать влиянием скоростей  ,
,  . Угол скольжения (дрейфа) объекта считаем равным нулю, то есть полагаем, что вектор скорости совмещен с продольной плоскостью объекта (
. Угол скольжения (дрейфа) объекта считаем равным нулю, то есть полагаем, что вектор скорости совмещен с продольной плоскостью объекта ( ). С учетом неравенства
). С учетом неравенства  считаем
считаем  .
.
Для этих условий 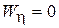 ,
,  (при левом вираже, то есть при
(при левом вираже, то есть при  вектор осестремительного ускорения совпадает с отрицательным направлением оси
вектор осестремительного ускорения совпадает с отрицательным направлением оси  , то есть направлен к левому борту объекта).
, то есть направлен к левому борту объекта).
С учетом сделанных упрощений уравнения движения прибора в условиях правильного виража можно представить:
 (1.17)
(1.17)
где  – угол отклонения маятника от вертикали при вираже объекта (если условие малости угла
– угол отклонения маятника от вертикали при вираже объекта (если условие малости угла  не выполняется, следует пользоваться формулой
не выполняется, следует пользоваться формулой  ).
).
Члены правой части системы уравнений (1.17) – нелинейные функции переменных  ,
,  и параметров движения объекта. Это делает уравнение (1.17) нелинейными и не позволяет составить их решение в общем виде. Однако нелинейность сигнум-функций проявляется лишь при нулевом значении аргументов, то при
и параметров движения объекта. Это делает уравнение (1.17) нелинейными и не позволяет составить их решение в общем виде. Однако нелинейность сигнум-функций проявляется лишь при нулевом значении аргументов, то при 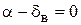 и
и 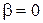 . При других значениях аргументов эти функции обращаются в положительную или отрицательную единицу, то есть нелинейных свойств не проявляют.
. При других значениях аргументов эти функции обращаются в положительную или отрицательную единицу, то есть нелинейных свойств не проявляют.
С учетом этой особенности составим решение уравнений (1.17) как линейных для значений переменных, удовлетворяющих условиям
 ,
,  (1.18)
(1.18)
и дополним эти решения качественным анализом выполнения условий (1.18) и установления знаков аргументов  и
и  сигнум-функций на различных участках движения гироскопа. Для участков движений, где одно или оба условия (1.18) не выполнены, определим движение гироскопа также на основе качественного анализа уравнений (1.17).
сигнум-функций на различных участках движения гироскопа. Для участков движений, где одно или оба условия (1.18) не выполнены, определим движение гироскопа также на основе качественного анализа уравнений (1.17).
Воспользуемся комплексной переменной  . С этой целью умножим первое уравнение на
. С этой целью умножим первое уравнение на  и сложим со вторым:
и сложим со вторым:
 (1.19)
(1.19)
Решение уравнения (1.19) для участков движения, на которых аргументы сигнум-функций знакоопределены, выглядит так:
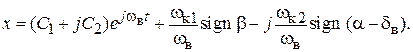
После замены, согласно формуле Эйлера, показательной функции тригонометрическими получим

 (1.20)
(1.20)
В исходных переменных  и
и  решение (1.20) примет вид
решение (1.20) примет вид
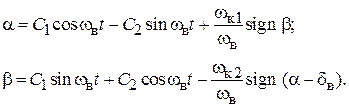 (1.21)
(1.21)
Для определения постоянных интегрирования зададим начальные условия. Предположим, что перед началом виража объекта главная ось гироскопа совпадает с вертикалью места, то есть при 
 . (1.22)
. (1.22)
Однако при выбранных начальных условиях не выполняется первое из условий (1.18). Следовательно, воспользоваться выражениями (1.21) для определения постоянных интегрирования нельзя. Проведем качественный анализ характера движения гироскопа при начальных условиях (1.22).
Из уравнений (1.17) следует, что в начальный момент после появления виража с учетом  возникает движение гироскопа по координате
возникает движение гироскопа по координате  со скоростью
со скоростью
 . (1.23)
. (1.23)
Действительно, из второго уравнения (1.17) видно, что в начальный момент
 .
.
С учетом того, что член 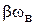 в начальный момент равен нулю, поскольку
в начальный момент равен нулю, поскольку  , получаем выражение (1.23), то есть накопление отрицательного угла
, получаем выражение (1.23), то есть накопление отрицательного угла  с постоянной скоростью
с постоянной скоростью  .
.
Каким будет движение по координате  ? Из первого уравнения системы (1.17) следует, что в начальный момент, то есть при
? Из первого уравнения системы (1.17) следует, что в начальный момент, то есть при  и
и 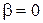 , система коррекции не включена,
, система коррекции не включена,  . Следовательно, движение по координате
. Следовательно, движение по координате  отсутствует.
отсутствует.
Действительно, в начальный момент времени, то есть при  , движение гироскопа по углу
, движение гироскопа по углу  определяется выражением
определяется выражением
 . (1.24)
. (1.24)
Если в силу тех или иных причин появляется сколько угодно малый угол  , отличный от нуля, например положительный (
, отличный от нуля, например положительный ( ), тотчас включается система коррекции
), тотчас включается система коррекции  , устраняющая положительный угол
, устраняющая положительный угол  . При отрицательном малом угле
. При отрицательном малом угле  появится, согласно (1.24), положительная скорость
появится, согласно (1.24), положительная скорость  , также устраняющая угол
, также устраняющая угол  .
.
Выясним, как изменится характер движения гироскопа по координате  с учетом члена
с учетом члена  по мере накопления угла
по мере накопления угла  .
.
Перепишем для этого первое уравнение системы (1.17) в виде
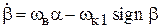 . (1.24а)
. (1.24а)
При увеличении со временем отрицательного угла  (
( ) член
) член  в выражении (1.24а) создает отрицательную скорость
в выражении (1.24а) создает отрицательную скорость  . Но при появлении угла
. Но при появлении угла  , удовлетворяющего условию
, удовлетворяющего условию  , включается система коррекции, появляется положительная скорость коррекции
, включается система коррекции, появляется положительная скорость коррекции  , устраняющая накопившийся отрицательный угол
, устраняющая накопившийся отрицательный угол  . Следовательно, при достаточно малых значениях угла
. Следовательно, при достаточно малых значениях угла  , то есть при условии
, то есть при условии  , отклонение гироскопа по координате
, отклонение гироскопа по координате  практически нулевое.
практически нулевое.
Характер движения изменится, когда нарастание отрицательного угла  приведет к нарушению условия
приведет к нарушению условия  . При достаточно большом (по модулю) значении угла
. При достаточно большом (по модулю) значении угла  , то есть при
, то есть при  , система коррекции уже не в состоянии удерживать гироскоп в положении
, система коррекции уже не в состоянии удерживать гироскоп в положении 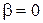 . В этом случае знак правой части равенства (1.24а) определяется знаком члена
. В этом случае знак правой части равенства (1.24а) определяется знаком члена  . Следовательно, при отрицательном значении
. Следовательно, при отрицательном значении  , удовлетворяющем условию
, удовлетворяющем условию  , появятся отрицательная скорость
, появятся отрицательная скорость  и отрицательный угол
и отрицательный угол  . Это произойдет при
. Это произойдет при  , где
, где  , то есть при
, то есть при 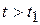 , где
, где  удовлетворяет условию
удовлетворяет условию  , а значит,
, а значит,
 ,
,
поскольку накопление угла  происходило с нулевого значения с постоянной скоростью
происходило с нулевого значения с постоянной скоростью  .
.
Таким образом, при 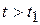 первое условие (1.18) выполняется. Если при этом второе условие (1.18) выполняется по-прежнему, то есть
первое условие (1.18) выполняется. Если при этом второе условие (1.18) выполняется по-прежнему, то есть  , то аргументы обеих сигнум-функций знакоопределены и дальнейшее движение происходит в соответствии с решениями (1.21).
, то аргументы обеих сигнум-функций знакоопределены и дальнейшее движение происходит в соответствии с решениями (1.21).
Поскольку выражения (1.21) отображают движение гироскопа лишь начиная с момента времени  , перепишем их в следующем виде
, перепишем их в следующем виде
 (1.25)
(1.25)
Постоянные интегрирования в (1.25) можно определить из условий при  :
:  ,
,  .
.
После подстановки этих значений в (1.25) получим:
 (1.26)
(1.26)
Для рассматриваемого участка движения при 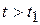 , как было показано при качественном анализе, угол
, как было показано при качественном анализе, угол  отрицателен. Поэтому
отрицателен. Поэтому  . В предположении
. В предположении  с учетом
с учетом  получим
получим  . С учетом приведенных значений сигнум-функций из (1.26) найдем:
. С учетом приведенных значений сигнум-функций из (1.26) найдем:  ,
,  . Из выражений (1.25) для этого участка движения следует, что:
. Из выражений (1.25) для этого участка движения следует, что:
 (1.27)
(1.27)
Исключив из выражений (1.27) время, получим следующее уравнение траектории движения вершины гироскопа на фазовой плоскости:
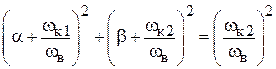 . (1.28)
. (1.28)
Траектория представляет собой окружность с радиусом, равным 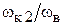 . Центр окружности в соответствии с (1.28) имеет координаты
. Центр окружности в соответствии с (1.28) имеет координаты
 .
.
 Для случая
Для случая  траектория показана на рис. 1.8. При
траектория показана на рис. 1.8. При 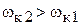 окружность дважды пересекает ось
окружность дважды пересекает ось  , а при
, а при  не доходит до оси
не доходит до оси  .
.
При правом вираже объекта, то есть при  угол отклонения маятника от истинной вертикали положительный. Вершина гироскопа вначале перемещается вдоль положительного направления оси
угол отклонения маятника от истинной вертикали положительный. Вершина гироскопа вначале перемещается вдоль положительного направления оси  , а при достижении значения
, а при достижении значения  начинает движение по окружности, лежащей в квадранте, ограниченном положительной полуосью
начинает движение по окружности, лежащей в квадранте, ограниченном положительной полуосью  и отрицательной полуосью
и отрицательной полуосью  .
.
Пользуясь рис. 1.8, нетрудно составить формулы максимальных погрешностей:
 (1.29)
(1.29)
По виду формул (1.29) не следует делать вывод о достижении погрешностями весьма больших величин при малой угловой скорости виража. Следует помнить, что показанная на рис. 1.8 траектория движения гироскопа получена для случая, когда 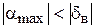 . При малой угловой скорости
. При малой угловой скорости  угол отклонения маятника от вертикали также мал и формулы (1.29) несправедливы.
угол отклонения маятника от вертикали также мал и формулы (1.29) несправедливы.
Если при движении по окружности (рис. 1.8) ось гироскопа достигает по координате  отклонения, равного углу отклонения маятника, то есть наступает равенство
отклонения, равного углу отклонения маятника, то есть наступает равенство  , нарушается второе условие (1.17). При этом для определения характера дальнейшего движения гироскопа нельзя пользоваться выражениями (1.27). Приходится снова определять характер движения на основе качественного анализа уравнений (1.17).
, нарушается второе условие (1.17). При этом для определения характера дальнейшего движения гироскопа нельзя пользоваться выражениями (1.27). Приходится снова определять характер движения на основе качественного анализа уравнений (1.17).
С этой целью перепишем (1.17):
 (1.30)
(1.30)
По первому из уравнений (1.30) легко определить скорость изменения угла  при
при  . Поскольку на рассматриваемом участке движения
. Поскольку на рассматриваемом участке движения  ,
,  и
и  :
:
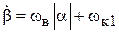 .
.
В этом выражении первый член правой части по модулю больше второго, поэтому знак  – отрицательный. Следовательно, отрицательный угол
– отрицательный. Следовательно, отрицательный угол  продолжает нарастать по модулю. Рассмотрим, как будет изменяться угол
продолжает нарастать по модулю. Рассмотрим, как будет изменяться угол  после достижения значения
после достижения значения 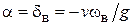 . Для этого проанализируем второе уравнение системы (1.30). При
. Для этого проанализируем второе уравнение системы (1.30). При  выключится система коррекции, то есть
выключится система коррекции, то есть  обратится в нуль. Первый член правой части рассматриваемого уравнения с учетом отрицательного значения угла
обратится в нуль. Первый член правой части рассматриваемого уравнения с учетом отрицательного значения угла  (
( ) даст положительную скорость изменения
) даст положительную скорость изменения  :
:  , то есть отрицательный угол
, то есть отрицательный угол  будет по модулю уменьшаться. Но как только угол
будет по модулю уменьшаться. Но как только угол  станет меньше
станет меньше  , снова включится система коррекции, которая создаст отрицательную скорость
, снова включится система коррекции, которая создаст отрицательную скорость  , превышающую положительную
, превышающую положительную  . Следовательно, система коррекции сохранит угол
. Следовательно, система коррекции сохранит угол  равным
равным  . Однако отрицательный угол
. Однако отрицательный угол  по модулю будет увеличиваться с постоянной скоростью
по модулю будет увеличиваться с постоянной скоростью  и в некоторый момент времени (обозначим его
и в некоторый момент времени (обозначим его  ) первый член правой части второго уравнения системы (1.30) –
) первый член правой части второго уравнения системы (1.30) –  достигнет по модулю значения
достигнет по модулю значения  и продолжит увеличиваться. Начиная с момента
и продолжит увеличиваться. Начиная с момента  система коррекции уже не сможет удерживать угол
система коррекции уже не сможет удерживать угол  равным
равным  , поскольку член
, поскольку член  по модулю превысит
по модулю превысит  . Следовательно, при
. Следовательно, при  :
:  ,
,  .
.
При отрицательном значении  (
( ) будет справедливо неравенство
) будет справедливо неравенство  и снова обеспечится знакоопределенность аргументов обеих сигнум-функций:
и снова обеспечится знакоопределенность аргументов обеих сигнум-функций:  ,
,  , то есть при
, то есть при  справедливы равенства
справедливы равенства  ,
,  .
.
Воспользуемся поэтому для  снова решениями (1.21). Перепишем эти решения в виде
снова решениями (1.21). Перепишем эти решения в виде
 (1.31)
(1.31)
Постоянные интегрирования  и
и  определим исходя из следующих граничных условий: при
определим исходя из следующих граничных условий: при 
 ,
,  .
.
После подстановки этих условий в (1.31):
 (1.32)
(1.32)
С учетом (1.32) выражение (1.31) перепишем в следующем виде:


Уравнение траектории для рассматриваемого участка движения таково:
 (1.33)
(1.33)
Таким образом, при  начиная с точки
начиная с точки  ,
,  вершина гироскопа движется по окружности радиусом
вершина гироскопа движется по окружности радиусом 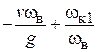 , центр которой в соответствии с (1.33) имеет координаты
, центр которой в соответствии с (1.33) имеет координаты  и
и  .
.

В целом траектория движения в рассматриваемом случае, то есть при 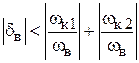 , состоит из следующих участков (рис. 1.9): отрезок прямой, совпадающий с отрицательным направлением оси
, состоит из следующих участков (рис. 1.9): отрезок прямой, совпадающий с отрицательным направлением оси  ; дуга окружности радиуса
; дуга окружности радиуса  ; отрезок прямой, параллельный оси
; отрезок прямой, параллельный оси  , соответствующий ординате
, соответствующий ординате 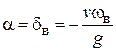 ; окружность радиуса
; окружность радиуса 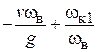 . В этом случае, как видно из рис. 1.9, максимальные погрешности прибора определяются выражениями
. В этом случае, как видно из рис. 1.9, максимальные погрешности прибора определяются выражениями  ,
,  .
.
Возможен, наконец, третий случай, когда угол  отклонения маятника от вертикали весьма мал и ось гироскопа достигает угла отклонения маятника, находясь на первом прямолинейном участке траектории, то есть случай, когда
отклонения маятника от вертикали весьма мал и ось гироскопа достигает угла отклонения маятника, находясь на первом прямолинейном участке траектории, то есть случай, когда  .
.
В такой ситуации после достижения гироскопом отклонения  дальнейшее его движение прекращается. Системы коррекции удерживают гироскоп в положении
дальнейшее его движение прекращается. Системы коррекции удерживают гироскоп в положении  ,
,  (рис. 1.10).
(рис. 1.10).
Пример.  ,
,  ,
,  .
.
Для этих параметров  . Точнее,
. Точнее, 

 ,
,  .
.
Следовательно,  ,
, 
 .
.
Из полученных формул максимальных значений виражных погрешностей рассматриваемой ГВ видно, что эти погрешности малы как при больших, так и при малых угловых скоростях  виража. В первом случае погрешность мала потому, что при больших отклонениях маятника она обратно пропорциональна
виража. В первом случае погрешность мала потому, что при больших отклонениях маятника она обратно пропорциональна  . При малых
. При малых  виражная погрешность ограничивается углом отклонения маятника, пропорциональным
виражная погрешность ограничивается углом отклонения маятника, пропорциональным  . Таким образом, наибольших значений погрешности достигают при средних значениях ускорений, то есть средних значениях угловой скорости виража (малое осестремительное ускорение
. Таким образом, наибольших значений погрешности достигают при средних значениях ускорений, то есть средних значениях угловой скорости виража (малое осестремительное ускорение  при большой угловой скорости
при большой угловой скорости  практически невозможно, поскольку большая угловая скорость
практически невозможно, поскольку большая угловая скорость  может быть достигнута при хорошей управляемости объекта, то есть при большей линейной скорости
может быть достигнута при хорошей управляемости объекта, то есть при большей линейной скорости  ). Поэтому можно для заданной скорости
). Поэтому можно для заданной скорости  рассчитать критическую угловую скорость
рассчитать критическую угловую скорость  , при которой виражная погрешность максимальна. Из сопоставления рис. 1.7 и 1.8 нетрудно сделать вывод, что критической угловой скорости
, при которой виражная погрешность максимальна. Из сопоставления рис. 1.7 и 1.8 нетрудно сделать вывод, что критической угловой скорости  соответствует случай, когда окружность траектории радиуса
соответствует случай, когда окружность траектории радиуса  касается в своей верхней точке линии
касается в своей верхней точке линии  , то есть при выполнении условия (рис. 1.11)
, то есть при выполнении условия (рис. 1.11)

 .
.
Отсюда:
 .
.
Максимальные значения погрешности при критической угловой скорости виража можно вычислить по формулам

Для параметров приведенного примера:



Для уменьшения виражных погрешностей целесообразно снижать скорость коррекции гироскопа. В практике для уменьшения виражных погрешностей авиационных ГВ используют радикальный способ – выключение поперечной коррекции на время виража самолета.
Поведение ГВ в условиях виража при выключенной поперечной коррекции рассмотрим в 1.7.


 и
и  по сравнению с постоянными угловыми скоростями коррекции
по сравнению с постоянными угловыми скоростями коррекции  и
и  , будем пренебрегать влиянием скоростей
, будем пренебрегать влиянием скоростей  ). С учетом неравенства
). С учетом неравенства  считаем
считаем  .
.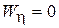 ,
,  (при левом вираже, то есть при
(при левом вираже, то есть при  вектор осестремительного ускорения совпадает с отрицательным направлением оси
вектор осестремительного ускорения совпадает с отрицательным направлением оси  , то есть направлен к левому борту объекта).
, то есть направлен к левому борту объекта). (1.17)
(1.17) – угол отклонения маятника от вертикали при вираже объекта (если условие малости угла
– угол отклонения маятника от вертикали при вираже объекта (если условие малости угла  не выполняется, следует пользоваться формулой
не выполняется, следует пользоваться формулой  ).
). ,
,  и параметров движения объекта. Это делает уравнение (1.17) нелинейными и не позволяет составить их решение в общем виде. Однако нелинейность сигнум-функций проявляется лишь при нулевом значении аргументов, то при
и параметров движения объекта. Это делает уравнение (1.17) нелинейными и не позволяет составить их решение в общем виде. Однако нелинейность сигнум-функций проявляется лишь при нулевом значении аргументов, то при 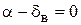 и
и 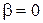 . При других значениях аргументов эти функции обращаются в положительную или отрицательную единицу, то есть нелинейных свойств не проявляют.
. При других значениях аргументов эти функции обращаются в положительную или отрицательную единицу, то есть нелинейных свойств не проявляют. ,
,  (1.18)
(1.18) и
и  . С этой целью умножим первое уравнение на
. С этой целью умножим первое уравнение на  и сложим со вторым:
и сложим со вторым: (1.19)
(1.19)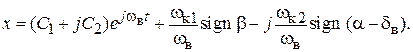

 (1.20)
(1.20)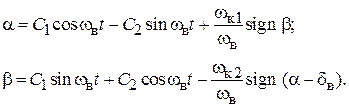 (1.21)
(1.21)
 . (1.22)
. (1.22) возникает движение гироскопа по координате
возникает движение гироскопа по координате  . (1.23)
. (1.23) .
.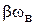 в начальный момент равен нулю, поскольку
в начальный момент равен нулю, поскольку  , получаем выражение (1.23), то есть накопление отрицательного угла
, получаем выражение (1.23), то есть накопление отрицательного угла  и
и  . Следовательно, движение по координате
. Следовательно, движение по координате  . (1.24)
. (1.24) ), тотчас включается система коррекции
), тотчас включается система коррекции  , устраняющая положительный угол
, устраняющая положительный угол  , также устраняющая угол
, также устраняющая угол  по мере накопления угла
по мере накопления угла 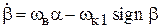 . (1.24а)
. (1.24а) ) член
) член  в выражении (1.24а) создает отрицательную скорость
в выражении (1.24а) создает отрицательную скорость  . Но при появлении угла
. Но при появлении угла  , включается система коррекции, появляется положительная скорость коррекции
, включается система коррекции, появляется положительная скорость коррекции  , устраняющая накопившийся отрицательный угол
, устраняющая накопившийся отрицательный угол  , отклонение гироскопа по координате
, отклонение гироскопа по координате  , система коррекции уже не в состоянии удерживать гироскоп в положении
, система коррекции уже не в состоянии удерживать гироскоп в положении  , появятся отрицательная скорость
, появятся отрицательная скорость  . Это произойдет при
. Это произойдет при  , где
, где  , то есть при
, то есть при 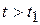 , где
, где  удовлетворяет условию
удовлетворяет условию  , а значит,
, а значит, ,
, , то аргументы обеих сигнум-функций знакоопределены и дальнейшее движение происходит в соответствии с решениями (1.21).
, то аргументы обеих сигнум-функций знакоопределены и дальнейшее движение происходит в соответствии с решениями (1.21). , перепишем их в следующем виде
, перепишем их в следующем виде (1.25)
(1.25) ,
,  .
. (1.26)
(1.26) . В предположении
. В предположении  с учетом
с учетом  получим
получим  . С учетом приведенных значений сигнум-функций из (1.26) найдем:
. С учетом приведенных значений сигнум-функций из (1.26) найдем:  ,
,  . Из выражений (1.25) для этого участка движения следует, что:
. Из выражений (1.25) для этого участка движения следует, что: (1.27)
(1.27)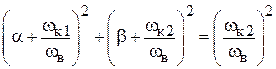 . (1.28)
. (1.28)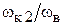 . Центр окружности в соответствии с (1.28) имеет координаты
. Центр окружности в соответствии с (1.28) имеет координаты .
. Для случая
Для случая  траектория показана на рис. 1.8. При
траектория показана на рис. 1.8. При 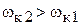 окружность дважды пересекает ось
окружность дважды пересекает ось  не доходит до оси
не доходит до оси  угол отклонения маятника от истинной вертикали положительный. Вершина гироскопа вначале перемещается вдоль положительного направления оси
угол отклонения маятника от истинной вертикали положительный. Вершина гироскопа вначале перемещается вдоль положительного направления оси  (1.29)
(1.29)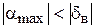 . При малой угловой скорости
. При малой угловой скорости  угол отклонения маятника от вертикали также мал и формулы (1.29) несправедливы.
угол отклонения маятника от вертикали также мал и формулы (1.29) несправедливы. , нарушается второе условие (1.17). При этом для определения характера дальнейшего движения гироскопа нельзя пользоваться выражениями (1.27). Приходится снова определять характер движения на основе качественного анализа уравнений (1.17).
, нарушается второе условие (1.17). При этом для определения характера дальнейшего движения гироскопа нельзя пользоваться выражениями (1.27). Приходится снова определять характер движения на основе качественного анализа уравнений (1.17). (1.30)
(1.30) :
: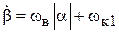 .
.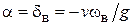 . Для этого проанализируем второе уравнение системы (1.30). При
. Для этого проанализируем второе уравнение системы (1.30). При  обратится в нуль. Первый член правой части рассматриваемого уравнения с учетом отрицательного значения угла
обратится в нуль. Первый член правой части рассматриваемого уравнения с учетом отрицательного значения угла  , то есть отрицательный угол
, то есть отрицательный угол  станет меньше
станет меньше  , снова включится система коррекции, которая создаст отрицательную скорость
, снова включится система коррекции, которая создаст отрицательную скорость  , превышающую положительную
, превышающую положительную  . Следовательно, система коррекции сохранит угол
. Следовательно, система коррекции сохранит угол  и в некоторый момент времени (обозначим его
и в некоторый момент времени (обозначим его  ) первый член правой части второго уравнения системы (1.30) –
) первый член правой части второго уравнения системы (1.30) –  и продолжит увеличиваться. Начиная с момента
и продолжит увеличиваться. Начиная с момента  система коррекции уже не сможет удерживать угол
система коррекции уже не сможет удерживать угол  по модулю превысит
по модулю превысит  . Следовательно, при
. Следовательно, при  :
:  ,
,  ) будет справедливо неравенство
) будет справедливо неравенство  и снова обеспечится знакоопределенность аргументов обеих сигнум-функций:
и снова обеспечится знакоопределенность аргументов обеих сигнум-функций:  ,
,  .
. (1.31)
(1.31) и
и  определим исходя из следующих граничных условий: при
определим исходя из следующих граничных условий: при 
 ,
,  .
. (1.32)
(1.32)

 (1.33)
(1.33) ,
,  вершина гироскопа движется по окружности радиусом
вершина гироскопа движется по окружности радиусом 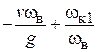 , центр которой в соответствии с (1.33) имеет координаты
, центр которой в соответствии с (1.33) имеет координаты  и
и  .
.
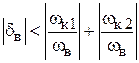 , состоит из следующих участков (рис. 1.9): отрезок прямой, совпадающий с отрицательным направлением оси
, состоит из следующих участков (рис. 1.9): отрезок прямой, совпадающий с отрицательным направлением оси  ; отрезок прямой, параллельный оси
; отрезок прямой, параллельный оси 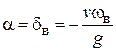 ; окружность радиуса
; окружность радиуса  ,
,  .
. .
. ,
,  (рис. 1.10).
(рис. 1.10). ,
,  ,
,  .
. . Точнее,
. Точнее, 

 ,
,  .
. ,
, 
 .
. при большой угловой скорости
при большой угловой скорости  ). Поэтому можно для заданной скорости
). Поэтому можно для заданной скорости  , при которой виражная погрешность максимальна. Из сопоставления рис. 1.7 и 1.8 нетрудно сделать вывод, что критической угловой скорости
, при которой виражная погрешность максимальна. Из сопоставления рис. 1.7 и 1.8 нетрудно сделать вывод, что критической угловой скорости  касается в своей верхней точке линии
касается в своей верхней точке линии  , то есть при выполнении условия (рис. 1.11)
, то есть при выполнении условия (рис. 1.11)
 .
. .
.






