
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оценка состояния эргатических систем управления
Для эффективного управления технической системой с человеком-оператором в контуре управления (эргатической системой управления) необходимо обеспечить должное состояние, как её технической, так и биологической составляющих. Своевременное обнаружение зарождающихся переходов систем из штатного состояния в нештатное – один из путей предупреждения и/или минимизации последствий нарушения штатного состояния систем управления. Оценка состояния (в смысле способности достижения цели управления) систем управления (СУ), как и их обобщенные характеристики, в общем случае определяются значениями n различных параметров, представляемых функциями одного или нескольких аргументов. К числу таких аргументов, в зависимости от типа рассматриваемой СУ, относят: количество элементов, узлов или сборочных единиц. При решении любой конкретной задачи учитываемые параметры СУ всегда образуют конечное множество параметров P i (i =1, 2, …, n), причем индексация параметров не ставится в зависимость от степени их важности. Характер учета отдельных параметров и их групп в процессе решения задачи, как правило, различен. Поэтому множество P обычно разбивают на ряд подмножеств P 1, P 2,..., P d в соответствии с используемыми признаками d ≤ n, если n – количество учитываемых параметров. Разбиение производится по следующим правилам:
В отдельных случаях решения практических задач допустимо трансформирование условия (4.5.1) к виду
при этом должны соблюдаться условия (4.5.1). Комплексный учет всех необходимых параметров при оценке состояния СУ практически перекрывает частные оценки, когда на базе одного или нескольких параметров строятся некоторые критерии работоспособности. Такие частные оценки могут использоваться лишь при синтезе относительно несложных СУ и только в случаях, когда на значения их параметров не накладываются жесткие ограничения. Когда все параметры P i определяются значениями всех аргументов x i (i =1, 2, …, k), при оценке состояния СУ рассматривается система функций:
Аргументы x j могут быть как дискретными, так и непрерывными, что определяется их физической сущностью, а также условиями функционирования СУ. Для СУ аргументы часто являются дискретными, что определяет и дискретность функций f i (i =1, 2, …, n). Так, например, если f 1 представляет вес узла СУ как её параметр и зависит от принятой разрядности x 1 и типа используемых для синтеза элементов x 2, то функция f 1 определена только на допустимых наборах аргументов x 1 и x 2 и является сугубо дискретной функцией.
Реальные СУ проектируются с учетом различных требований, накладываемых на значения параметров. В общем случае эти ограничения являются двухсторонними, поэтому система функций (38.1) дополняется следующей системой неравенств:
где A i и B i (i =1, 2, …, n) – некоторые числа, определяющие соответственно нижний и верхний пределы допустимых значений i -го параметра. Для различных параметров, используемых на практике, характер ограничений может не совпадать. Это обстоятельство учитывается при решении конкретных задач, в частности, характер ограничений, как один из признаков, учитывается при разбиении множества параметров на подмножества в соответствии с (4.5.1). Общий критерий состояния СУ формируется с учетом системы неравенств (38.2), которая выражает основные требования, предъявляемые к данной СУ. При этом используются допустимые значения параметров, удовлетворяющие условиям (4.5.2). Структура СУ оптимальна в том случае, когда все её параметры, учитываемые при синтезе, имеют оптимальные значения; в противном случае она относится к неоптимальным структурам. Таким образом,
если A i≤ P i≤ B i для всех i Соотношение (4.5.3) представляет собой признаки выявления оптимальной в принятом смысле структуры СУ. Эти признаки оказываются основными для формирования общего критерия состояния СУ и выявления условий существования оптимальной её структуры. Если все аргументы x i берутся с тем или иным шагом дискретности, что отвечает реальным случаям постановки задачи выявления оптимальных структур, то множество возможных значений любого x i конечно; множество N всех возможных наборов аргументов также конечно, а его мощность не превосходит некоторую величину H. Обозначим через N i
Структура СУ оптимальна, если существует хотя бы один такой набор аргументов, на котором все параметры, учитываемые при решении конкретной задачи и задаваемые функциями f i, принимали бы оптимальные значения. С учетом введенных обозначений это условие существования оптимальной структуры записывается в виде
Таким образом, оптимальная структура СУ существует, если объединение всех пересечений множеств N i, т. е. множеств наборов аргументов, на которых отдельные параметры принимают оптимальные значения, не являются пустым множеством. Условие (4.5.4) представляет собой и общий критерий работоспособности, так как позволяет разделить СУ или их структуры по степени пригодности в конкретных условиях. Кроме того, оно может служить критерием выявления оптимальных структур СУ; при синтезе и оптимизации его применение позволяет исключить из рассмотрения структуры, не отвечающие предъявляемым требованиям. Эффективность применения полученного критерия зависит от достоверности и полноты функциональных зависимостей для всех параметров. Большое значение имеет также конкретно реализуемый алгоритм, построенный на базе общего алгоритма выявления оптимальных структур, но полученный общий критерий не обеспечивает непосредственного определения лучших из числа выявленных структур СУ. Общий алгоритм выявления оптимальных структур, базирующийся на условии (4.5.4), строится для ограниченного числа учитываемых параметров, представляемых функциями нескольких аргументов (например, учитываются время реализации алгоритма, вес, габариты, энергоёмкость, вероятность безотказной работы, рассчитываемые в зависимости от количества элементов, необходимых для синтеза различных структур СУ, и характеристик стандартных элементов, приемлемых для данных конкретных условий эксплуатации СУ). Он предусматривает: 1) определение наборов аргументов N i, на которых функции, представляющие параметры СУ, удовлетворяют условиям (4.5.2); 2) кодирование множеств N i для обеспечения эффективного использования принимаемых методов решения задачи выявления оптимальных структур; и 3) выявление пересечений множества N i, т. е. выявление оптимальных структур систем. При этом необходимо находить значения функций на всех наборах аргументов и сравнивать их с их допустимыми величинами. Так, для вычисления одного значения функции f i требуется выполнить G i операций. Общее же количество операций, выполняемых при решении задачи с учетом односторонних ограничений, равно
тогда как при двухсторонних ограничениях для всех параметров, оно оценивается по формуле
Решение задачи кодирования осуществляется путём присвоения наборам N i условных номеров, формируемых из двух частей, одна из которых представляет признак функции, а другая – номер набора, на котором эта функция принимает оптимальное значение. Выявление пересечений множеств N i, т. е. реализация заключительной части алгоритма, сводится к сравнению кодов наборов, имеющих различные признаки.
Общий критерий состояния СУ не позволяет выявлять максимально приемлемые, в конкретных условиях, оптимальные структуры, поэтому приходится общие критерии дополнять частными критериями, при формировании которых не обязателен учет всех возможных параметров СУ. Использование частных критериев в качестве основных при оптимизации структур СУ допустимо в тех случаях, когда на значения отдельных параметров не накладываются жесткие ограничения, а указывается лишь направление желаемого их изменения. Кроме того, они могут использоваться для предварительной оценки состояния известных или возможных структур, а также при решении частных задач синтеза СУ. Примером частного критерия могут служить соотношения P i≤ P iдоп; P 2 опт= P 2min, которые, в частности, отвечают случаю выявления структуры со временем реализации алгоритма, не большем допустимого, и минимальным аппаратным составом. К частным критериям во многих случаях решения практических задач относятся и функциональные критерии, которые при синтезе СУ используются как частные, позволяющие выявить лучшую из общеоптимальных структур, выявленных по общему критерию. Тогда система (38.6) трансформируется в
где j Функциональные критерии в общем случае вводятся для определения данной структуры СУ. Она считается подходящей или лучшей, если функционал (может быть линейным или нелинейным)
где W i – некоторые коэффициенты, имеет экстремум или отличается от некоторого значения не более чем на установленную величину. При использовании нелинейных функционалов и незначительном числе учитываемых параметров, в большей степени учитывается взаимосвязь параметров системы. При проведении сравнительных оценок различных структур СУ нелинейные функциональные критерии строятся без учета коэффициентов W i при сложной размерности, определяемой размерностью учитываемых параметров и видом принимаемых зависимостей. Линейный функциональный критерий рассчитывается с учетом нормированных значений функций f ij, взятых с определенными весовыми коэффициентами w i, по
где F i0 – нормирующий делитель.
Параметры СУ могут представляться полиномами m -й степени от x, тогда и функциональный критерий (4.5.9) представляется полиномом, степень которого определяется максимальной степенью исходных полиномов, например степенью m. Использование линейного критерия при оценке состояния СУ, т. е. и при определении строго оптимальных структур, в этих случаях сводится к решению линейных алгебраических уравнений (m –1)-го порядка вида
Одним из основных вопросов, решаемых при формировании критерия (38.9), является вопрос об определении или назначении величин весовых коэффициентов w i и нормируемых делителей F i0. Если величина F i0 назначается только для получения безразмерных функциональных критериев без должного учета ограничений (4.5.3), то имеет место система зависимостей
где С i и С’ i – некоторые постоянные величины, причем
Поэтому при формировании критерия (4.5.10) отдельные параметры «взвешиваются» дважды. Устранение двойного «взвешивания» может быть обеспечено назначением таких w i, которые дополнительно учитывают значения уже выбранных или назначенных величин F i0. а так как это не всегда возможно, то значения w i и F i0 определяются без использования дополнительных функциональных связей. Учет требования о необходимости приведения нормируемых функций f ij к определенному уровню приводит к определению значений нормирующих делителей F i0. При проведении расчетов по (4.5.10) принимаются во внимание только те значения функций, которые удовлетворяют условиям (4.5.4). Поэтому для их нормирования и приведения к определенному уровню необходимо выполнение условий
при пропорциональной связи между F i0 и A i(B i), выражаемой через
Если на параметры СУ заданы односторонние ограничения, то принимается A i=0 или B i=0 при вычислениях по (4.5.12), а если на параметры заданы двухсторонние ограничения, то значения F i0 определяются по (4.5.11) и (4.5.12). Большинство параметров, характеризующих состояние (функциональную готовность) СУ, непосредственно выражаются величинами, значения которых должны быть минимальными из возможных для оптимальных структур. При этом значения всех параметров не должны отличаться от желаемых больше, чем на заданные величины, т. е.
где D i – желаемое значение i -го параметра, Δ D i – допустимое отклонение значения i -го параметра от желаемого или заданного. Для упрощения последующих действий целесообразно принять
В реальных условиях функции f ij принимают оптимальные значения, равные D i, при различных значениях аргумента х, но при условии, что относительные пределы изменения значений функционала не превосходят средние допустимые пределы составляющих его функций. Тогда
Совокупность условий и ограничений (4.5.13)÷(4.5.16) обеспечивает решение общей задачи выявления оптимальных структур СУ. Соответствующий алгоритм предусматривает такую последовательность действий:
а) определение исходных, для расчета на последующих этапах, величин Δ Ф согласно (4.5.16) с заданием шага Δ х, определяющего частость получения решений; б) формирование функционала вида (4.5.10) с учетом соотношений (4.5.13); в) расчет значений функционала (4.5.10) с шагом Δ х и выявление функционалов, удовлетворяющих условию (4.5.15), с фиксацией значений аргумента x i, отвечающего выделенным значениям Ф; г) для каждого Ф 0, удовлетворяющего условию (4.5.16), рассчитываются значения всех составляющих его функций f ij; д) проверка всех наборов f ij, найденных в г), условиям (4.5.15); и е) выявление случаев удовлетворения условиям (4.5.14) и (4.5.16), т. е. выявление оптимальных структур СУ по
для всех i Все части алгоритма последовательно реализуются для различных наборов условий j. Если по (4.5.16) оптимальные структуры не выявлены, то, последовательно увеличивая значения Δ Ф, допустимо выявление квазиоптимальных структур различных градаций. Выше сказанное применимо для СУ, например, летательного аппарата с управлением автопилотом, но автоматизированные системы управления, т. е. системы с человеком-оператором в контуре управления, в силу значительного объема информации о состоянии человека пока оценить предварительно и аналитически не представляется возможным. Например, при управлении летательным аппаратом пилотом оценку состояния системы производить проще, с учетом человеческого фактора, инструментально и менее инерционно. Раздельная оценка состояния технической составляющей эргатической системы управления и её биологической части позволяет минимизировать временные и инструментальные затраты и предупредить, в масштабе реального времени, выход системы из штатного состояния. Первые, пока локальные, проверки целесообразности оценки текущего состояния пилота уже подтвердили целесообразность оценки состояния пилота. Таким образом, оценка текущего состояния (функциональной готовности) технического оборудования и человека-оператора, как интегрированной системы, позволяет оперативно принять адекватные меры по недопущению и/или минимизации последствий перехода системы в нештатное состояние. Предлагаемый метод является достаточно универсальным и может быть рекомендован для нормализации ситуаций на транспорте, преимущественно в авиации. Эволюционный процесс системы математически описывается векторным полем в фазовом пространстве её состояний. Точка P фазового пространства задает состояние системы, а приложенный в точке A вектор F отражает скорость изменения состояния системы. Если приложенный вектор F А=0, тогда точка А→P – точка равновесия, состояние системы не меняется с течением времени. Однако с течением времени t, при определенных условиях, в системе могут установиться колебания, а равновесное состояние становится неустойчивым. Установившиеся колебания системы изображаются замкнутой кривой на фазовой плоскости, отражающей предельный цикл. Кривые в фазовом пространстве, образованные последовательными состояниями процесса, называют фазовыми кривыми. В окрестности положения равновесия, как показал еще А. Пуанкаре, поведение фазовых кривых отображаются фазовыми портретами (см. рис. 4.5.1) типа «фокус» (а, д), «узел» (б, г), для устойчивых (направление вектора к точке P; а и б), «седло» (в) и фазовыми портретами типа «узел» и «фокус» для неустойчивых (направление вектора от точки P; г и д).
Рис. 4.5.1 Если устойчивое положение равновесия описывает установившийся режим в реальной системе, то его слияние с неустойчивым положением равновесия система должна совершить скачок, перескочив на совершенно другой режим: при изменении параметра равновесное состояние в рассматриваемой окрестности исчезает. Скачки этого рода и привели к термину «теория катастроф». При столкновении положения равновесия («узел») с неустойчивым положением («седлом») оба положения исчезают. Таким образом перестройка через «седло-узел» ведет к скачкообразному изменению режима системы. При этом возможны два варианта нового состояния системы: А. При изменении параметра системы (например, А) из положения равновесия рождается предельный цикл (радиус порядка ε 0.5, когда значение параметра А отличается от бифуркационного на ε), а устойчивость равновесия переходит к циклу, само же равновесие становится неустойчивым. Б. В положении равновесия вырождается неустойчивый предельный цикл; область притяжения положения равновесия уменьшается с ним до нуля, после чего цикл исчезает, а его неустойчивость передается равновесному новому состоянию. Если новое положение равновесия – установившийся режим в реальной системе, то при изменении параметра (А) в случаях А и Б наблюдаются следующие явления. А. После потери устойчивости равновесия установившимся режимом оказывается колебательный периодический режим (рис. 4.5.2, а), амплитуда колебаний которого пропорциональна корню квадратному из закритичности (отличия параметра А от критического значения, при котором равновесие теряет устойчивость), при этом отрезок времени t 0÷ t 2 характеризует квазистационарное приближение (инерционность переходного процесса), а участок временной оси t 1– t 2 – время потери устойчивости. Этот вид потери устойчивости называют мягкой потерей устойчивости, так как установившийся колебательный режим при малой закритичности параметра А мало отличается от состояния равновесия. Б. Перед тем как установившийся режим теряет устойчивость, область притяжения t 0– t 1 (см. рис. 4.5.2, б) значительно сокращается и случайные внешние возмущения переводят систему из этой области в другую еще до полного исчезновения области притяжения. Этот вид потери устойчивости называют жесткой потерей устойчивости, так как система переходит из стационарного режима скачком в иное состояние (иной режим движения, он может быть устойчивым стационарным, колебательным или более сложным).
После того как параметр А прошел бифуркационное значение, соответствующее рождению цикла, т. е. мягкому возникновению автоколебаний, система остается в окрестности потерявшего устойчивость состояния равновесия еще некоторое время, за которое параметр А успевает измениться на конечную величину. И лишь затем система скачком переходит на родившийся в момент бифуркации автоколебательный режим, так что потеря устойчивости кажется жесткой. Таким образом сложные колебания в электронных системах управления могут быть связаны как со случайными внешними (климатическими, радиационными и др.) воздействиями, так и с внутренними процессами деградации элементов и узлов систем, а в частности и с основными уравнениями задачи управления.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-23; просмотров: 89; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.189.22.136 (0.051 с.) |
 P ξ=0, f 1(x 1, x 2, …, x k), η
P ξ=0, f 1(x 1, x 2, …, x k), η  {1, 2, …, d }, ξ
{1, 2, …, d }, ξ 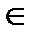 {1, 2, …, d };
{1, 2, …, d };
 P η= P, P η≠0.
P η= P, P η≠0.
 N множество наборов аргументов, на которых функция f i, представляющая i -й параметр, принимает оптимальные значения. Для любого i количество таких наборов практически всегда меньше величины H.
N множество наборов аргументов, на которых функция f i, представляющая i -й параметр, принимает оптимальные значения. Для любого i количество таких наборов практически всегда меньше величины H. N i≠0, i
N i≠0, i  G i),
G i),
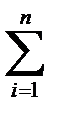 w i F i0-1 f ij(x),
w i F i0-1 f ij(x),
 (q +1) a q+1 x q=0.
(q +1) a q+1 x q=0.
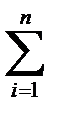 w i=1.
w i=1.
 а б в г д
а б в г д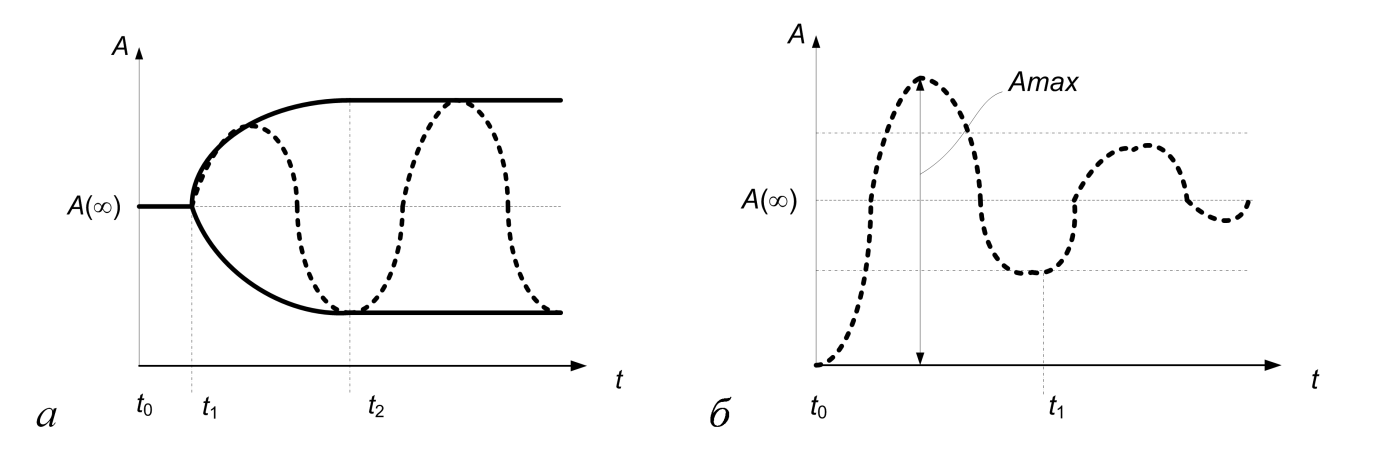 Рис. 4.5.2
Рис. 4.5.2


