
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Правила принудительного ранжированияСтр 1 из 25Следующая ⇒
1) Наименьшему числовому значению начисляется ранг 1. 2) Наибольшему числовому значению – ранг, равный n – количеству ранжируемых величин. 3) Если несколько числовых значений равны, то им начисляется ранг, равный среднему значению из тех рангов, которые они получили бы, если бы не были равны. 4) Правильность начисления рангов проверяется формулой:
где n – количество ранжируемых величин. 5) Не рекомендуется ранжировать более 20 величин, поскольку в этом случае ранжирование в целом окажется малоустойчивым. 6) При необходимости ранжирования достаточно большого числа объектов их следует объединять по какому-либо признаку в достаточно однородные классы, а затем уже ранжировать полученные классы. Пример начисления рангов для результатов тестирования представлен в таблице 2.3.
Таблица 2.3
В примере встречаются три значения 75, в обычной нумерации они получили бы ранг 3, 4, 5. Таким образом, каждое из них получает ранг, равный Для проверки правильности начисления рангов найдем:
РАСПРЕДЕЛЕНИЕ ЧАСТОТ При описании общей картины результатов теста список студентов из таблицы можно сократить, классифицируя баллы по распределению частот, иногда называемому распределением. Числа, показывающие, сколько раз варианты встречаются в данной совокупности, называются частотами, или весами вариант. Они обозначаются fi и имеют индекс «i», соответствующий номеру переменной. Частость (относительная частота) – доля каждой частоты fi в общем объеме выборки n:
В таблице 2.4 приведен пример нахождения частоты и частости результатов тестирования из таблицы 2.3. В случае большого диапазона разброса данных имеет смысл обобщение данных в виде группирования по интервалам. Правила выбора количества интервалов не существует, но предпочтительно группировать по 12-15 интервалам (классам).
Ширина интервалов (класса) должна быть одинаковой и равной
где h – ширина интервалов; k – количество классов; Xmax – максимальное значение из данных; Xmin – минимальное значение из данных.
Таблица 2.4
Количество классов выбирается таким образом, чтобы ширина была целым числом. Задача 2.1 Данные из таблицы 2.4 необходимо разбить на интервалы, найти середины интервалов, а также частоту и частость в интервалах. Максимальный балл равен 90 баллам, минимальный – 71. Ширина определяется по формуле (2.3):
Для того чтобы ширина была целым числом, количество интервалов должно быть или 4, или 5, или 10. Найдем ширину интервалов при количестве интервалов, равном пяти:
Определение середины интервала состоит в усреднении зафиксированных границ интервала. Например, для первого интервала середина будет (74+71)/2=72,5. Занесем все вычисления в таблицу 2.5.
Таблица 2.5
СТАТИСТИЧЕСКИЕ РЯДЫ
Особую форму группировки данных представляют так называемые статистические ряды, или числовые значения признака, расположенного в определенном порядке. В зависимости от того, какие признаки изучаются, статистические ряды делят на атрибутивные, вариационные, ряды динамики, регрессии, ряды ранжированных значений признаков и ряды накопленных частот. Наиболее часто в психологии используются вариационные ряды, ряды регрессии и ряды ранжированных значений признаков. Вариационным рядом распределения называют двойной ряд чисел, показывающий, каким образом числовые значения признака связаны с их повторяемостью в данной выборке. Например, результаты вступительного тестирования оказались следующими: 71, 75, 84, 75, 87, 84, 75, 88, 90, 88. Как видим, некоторые цифры попадаются в данном ряду по несколько раз. Следовательно, учитывая число повторений, данные ряда можно представить в более удобной, компактной форме:
Это и есть вариационный ряд. Числа, показывающие, сколько раз отдельные варианты встречаются в данной совокупности, называются частотами, или весами, вариант. Они обозначаются строчной буквой латинского алфавита и имеют индекс «i», соответствующий номеру переменной в вариационном ряду. Общая сумма частот вариационного ряда равна объему выборки, т.е.
Частоты можно выражать и в процентах. При этом общая сумма частот или объем выборки принимается за 100%. Процент каждой отдельной частоты или веса подсчитывается по формуле:
Процентное представление частот полезно в тех случаях, когда приходится сравнивать вариационные ряды, сильно различающиеся по объемам. Например, при тестировании школьной готовности детей города, поселка городского типа и села были обследованы выборки детей численностью 1000, 300 и 100 человек соответственно. Различие в объемах выборок очевидно. Поэтому сравнение результатов тестирования лучше проводить, используя проценты частот. Приведенный выше ряд (2.4) можно представить по-другому. Если элементы ряда расположить в возрастающем порядке, то получится так называемый ранжированный вариационный ряд:
Подобная форма представления (2.6) более предпочтительна, чем (2.4), поскольку лучше иллюстрирует закономерность варьирования признака. Частоты, характеризующие ранжированный вариационный ряд, можно складывать или накапливать. Накопленные частоты получаются последовательным суммированием значений частот от первой частоты до последней. В качестве примера вновь обратимся к ряду 2.6. Преобразуем его в ряд 2.7, в котором введем дополнительную строчку и назовем ее «кумуляты частот».
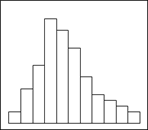
ПОНЯТИЕ РАСПРЕДЕЛЕНИЯ И ГИСТОГРАММЫ В статистике под рядом распределения понимают распределение частот по вариантам. Измеренные величины признака в выборке варьируют в пределах от минимального до максимального значения. Этот предел разбивают на так называемые классовые интервалы, которые, в зависимости от конкретных данных, могут быть как равными по величине, так и неравными. Существует четыре общих метода графического представления распределения частот: гистограмма, полигон распределения и сглаженная кривая, кумулятивный полигон. Если по оси абсцисс – OX откладывать величины классовых интервалов, а по оси ординат – OY – величины частот, попадающих в данный классовый интервал, то получается так называемая гистограмма распределения частот. При этом над каждым классовым интервалом строится колонка или прямоугольник, площадь которого оказывается пропорциональной соответствующей частоте. Пример построения гистограммы представлен на рисунке 2.1.
Рис.2.1. Гистограмма результатов тестирования 43 абитуриентов.
Гистограмма представляет собой графическое изображение данного частотного распределения. Виды распределения представлены на рисунке 2.2. Построение полигона распределения во многом напоминает построение гистограммы. В гистограмме каждый столбец заканчивается горизонтальной линией, причем на высоте, соответствующей частоте в этом разряде. А в полигоне он заканчивается точкой над серединой своего разрядного интервала на той же высоте. Далее точки соединяются отрезками прямых (см. рисунок 2.3). – это и будет полигон распределения. Если эти же точки соединить плавной линией – получим сглаженную кривую распределения (см. рисунок 2.4). Если по оси OY откладывать кумуляты частот, то получим кумулятивный полигон (см. рисунок 2.5).
а) Обычный тип б) Гребенка
в) Положительно г) Распределение с скошенное распределение обрывом слева
д) Плато е) Двухпиковый тип
ж) Распределение с изолированным пиком
Рис. 2.2. Виды гистограмм.
Рис.2.3. Полигон распределения, представляющий результаты тестирования 43 абитуриентов.
Рис.2.4. Кривая распределения результатов тестирования 43 абитуриентов.
Рис.2.5. Кумулятивный полигон.
? ВОПРОСЫ И УПРАЖНЕНИЯ
1. Дайте определение следующим понятиям: группировка данных, ранжирование, ранг, частота, частость, статистический и вариационный ряды, распределение, гистограмма, полигон распределения и сглаженная кривая. 2. В исследовании 3. Эта задача – на построение группового распределения частот. Следующие данные представляют собой оценки 75 взрослых людей в тесте на определение коэффициента интеллектуальности Стенфорда-Бине: В задаче: · сгруппируйте результаты наблюдений; · определите частоту и частость показателей; · выберите интервал группирования разрядов; · постройте распределение сгруппированных частот, полигон распределения и сглаженную кривую.
ТЕМА 3
МЕРЫ ЦЕНТРАЛЬНОЙ ТЕНДЕНЦИИ Свойства совокупности данных можно представить в форме графиков или таблиц. Часто график или таблица говорят больше, чем мы хотим или должны знать, а передаваемая информация может оцениваться временем, потребным на сообщение. Поэтому обычно используется для описания совокупности данных только два-три свойства. Эти свойства (например, «значение», наиболее часто встречающееся среди результатов, или разброс значений) могут быть описаны показателями, известными как «статистики свертки», «методы оценки средних величин» или «меры центральной тенденции».
Термин «статистики» совокупности данных используется при описании выборочной совокупности данных. Если речь идет о генеральной совокупности, то ее показатели именуются «параметрами».
МОДА
Наиболее просто получаемой мерой центральной тенденции является мода. Мода – это значение во множестве наблюдений, которое встречается наиболее часто. В совокупности значений (1, 2, 2, 7, 8, 8, 8, 10) модой является 8, потому что оно встречается чаще любого другого значения. Мода представляет собой наиболее частое значение (в данном примере 8), а не частоту этого значения (в примере равную 3). Однако не всякая совокупность значений имеет единственную моду в строгом понимании этого определения, поэтому рабочее определение моды содержит особенности и соглашения. 1. В случае, когда все значения в группе встречаются одинаково часто, принято считать, что группа оценок не имеет моды. Так, в группе (0,2; 0,2; 2,3; 2,3; 4,1; 4,1) моды нет. 2. Когда два соседних значения имеют одинаковую частоту и они больше частоты любого другого значения, мода есть среднее этих двух значений. Итак, мода группы значений (0,1, 1, 2, 2, 2, 3, 3, 3, 4) равна 2,5. 3. Если два несмежных значения в группе имеют равные частоты и они больше частот любого значения, то существуют две моды. В группе значений (5, 7, 7, 7, 10, 11, 12, 12, 12, 17) модами являются и 7 и 12. В таком случае говорят, что группа оценок является бимодальной. Замечание Большие множества данных часто рассматриваются как бимодальные, когда они образуют полигон частот, похожий на спину бактриана – верблюда двугорбого, даже если частоты на двух вершинах не строго равны. Это незначительное искажение определения вполне оправданно, ибо термин «бимодальный» допустим и удобен для описания. Можно условиться различать большие и меньшие моды. Наибольшей модой в группе называется единственное значение, которое удовлетворяет определению моды. Однако во всей группе может быть и несколько меньших мод. Эти меньшие моды представляют собой, в сущности, локальные вершины распределения частот. Например, на рисунке 3.1 наибольшая мода наблюдается при значении 6, а меньшие – при 3,5 и 10.
Рис. 3.1. Распределение частот тестовых оценок с наибольшей модой 6 и меньшими модами 3,5 и 10.
МЕДИАНА
Медиана (Md) – значение, которое делит упорядоченное множество данных пополам, так что одна половина значений оказывается больше медианы, а другая – меньше.
Вычисление медианы 1. Если данные содержат нечетное число различных значений, то медиана есть среднее значение для случая, когда они упорядочены. Например, в группе (17, 19, 21, 24, 27) медиана равна 21. 2. Если данные содержат четное число различных значений, то медиана есть точка, лежащая посредине между двумя центральными значениями, когда они упорядочены. В группе (3, 11, 16, 20) медиана вычисляется как (11+ 16)/2 = 13,5. 3. Если в данных есть объединенные классы, особенно в окрестности медианы, возможно, потребуется табулирование частот. В таких случаях придется интерполировать внутри разряда значений. Задача 3.1 Пусть, например, 36 значений, упорядоченных от 7,0 до 10,5, имеют следующее распределение:
Оценкой медианы будет величина n /2, равная 18-му значению снизу. Медиана будет находиться по формуле:
(3.1) В задаче 3.1: § фактическая нижняя граница интервала равна 8,25; § ширина интервала медианы равна 0,5; § оценка медианы n /2 = 36/2 =18; § частота, накопленная к интервалу медианы, равна13; § частота в интервале медианы равна 10. Подставляя найденные значения в формулу (3.1), получим: Md = 8,25 + 0,5× (18-13) /10 = 8,5.
СРЕДНЕЕ
Третья мера – среднее выборочное, называемое иногда «средним», «арифметическим средним» или «математическим ожиданием». Среднее выборочной совокупности п значений определяется как
или:
Если даны значения и частоты их повторения, то среднее значение определяется формулой:
Найдем, например, среднее для значений из задачи 3.1:
Если даны значения в интервале, тогда за xi берутся середины интервалов. Соответствующим параметром генеральной совокупности будет средняя генеральной совокупности m, которая вычисляется по формуле (3.4), аналогичной формуле (3.2):
где N – численность или объем генеральной совокупности. Свойства среднего 1) Сумма всех отклонений от среднего значения равна нулю:
2) Если константу прибавить к каждому значению, то среднее увеличится ровно на эту константу:
3) Если каждое значение умножить на константу с, то среднее увеличится в с раз:
4) Сумма квадратов отношений значений от их среднего значения меньше суммы квадратов отклонений от любой другой точки:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 485; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.191.22 (0.092 с.) |
 , (2.1)
, (2.1) – сумма всех рангов,
– сумма всех рангов, .
. ,
,  .
.
 . (2.2)
. (2.2) , (2.3)
, (2.3) .
. .
.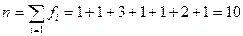 .
. . (2.5)
. (2.5)













 8,0
8,0


 . (3.2)
. (3.2) . (3.3)
. (3.3)
 , (3.4)
, (3.4) . (3.5)
. (3.5) . (3.6)
. (3.6) . (3.7)
. (3.7) . (3.8)
. (3.8)


