
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Остаточным членом в форме Пеано
Джузеппе Пеано (1858-1932) – итальянский математик 1. Возьмём произвольную функцию 2. Пусть функция 3. Тогда многочлен
называется многочленом Тейлора для функции 4. Хотя многочлен 5. В данном случае многочлен 6. Разность 7. Изучим поведение разности 8. Прежде всего, функция 9. При этом 10. Действительно,
11. Рассмотрим отношение 12. Для раскрытия этой неопределённости следует n раз применить первое правило Лопиталя (первую теорему или первое правило Лопиталя) при x®x0:
13. Отсюда следует, что остаточный член Обозначают это условно так: 14. Тогда можно записать 15. Эта формула называется формулой Тейлора с остаточным членом в форме Пеано. 16. Остаточный член формулы Тейлора — это разность 17. Отсюда дифференциальная форма формулы Тейлора будет иметь вид
Формула Тейлора для функции одной переменной с Остаточным членом в форме Лагранжа Считаем, что функция
Теорема. Для любого где Доказательство 1. Зафиксируем 2. Очевидно, что 3. Кроме того
4. Применим теорему Коши к функциям
ч.т.д. 5. Аналогично проводится доказательство для отрезка [x;x0].
Формула Тейлора для функции одной переменной с
Остаточным членом в форме Коши Считаем, что функция Теорема. Для любого Доказательство 1. Зафиксируем
2. Ясно, что 3. Кроме того,
4. Применим теорему Коши к функциям
5. Так как где 6. Тогда ч.т.д. Замечание 1. C учётом последних двух теорем, формула Тейлора с остаточным членом в форме Лагранжа и Коши примет вид:
где 2. При или форме Пеано: Разложение элементарной функции ex по формулам Тейлора и Маклорена Рассмотрим пример приближенного представления элементарной функции ex с помощью формулы Маклорена. 1. Формула Маклорена для где 2. Так как
3. А 4. Формула Маклорена с остаточным членом в форме Лагранжа примет вид: 5. Формула Маклорена с остаточным членом в форме Пеано имеет вид:
6. Для функции ex формула Маклорена с остаточным членом в форме Пеано примет вид: Разложение элементарных функций sin x, cos x, (1+x)α
|
|||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 980; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.143.239 (0.02 с.) |
 , определённую на
, определённую на  и не являющуюся целым многочленом.
и не являющуюся целым многочленом. имеет производные до n го порядка включительно в некоторой точке
имеет производные до n го порядка включительно в некоторой точке  .
.
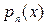 и
и  , функция
, функция  .
. , очевидно, будет погрешностью, допускаемой при замене
, очевидно, будет погрешностью, допускаемой при замене  на
на  .
. в окрестности точки
в окрестности точки 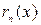 n раз дифференцируема в окрестности точки
n раз дифференцируема в окрестности точки  и
и  в точке
в точке  , следовательно,
, следовательно,
 , x ® x0. Оно представляет собой неопределенность вида
, x ® x0. Оно представляет собой неопределенность вида  .
.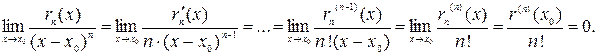
 в точке
в точке 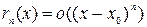 при x®x0.
при x®x0.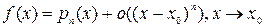 или
или  или
или  .
. .
. ,
,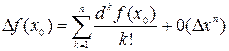 ,
,  — формула Тейлора для функции в дифференциальном виде с остаточным членом в форме Пеано.
— формула Тейлора для функции в дифференциальном виде с остаточным членом в форме Пеано. остаточный член формулы Тейлора может быть представлен в виде или в форме Лагранжа:
остаточный член формулы Тейлора может быть представлен в виде или в форме Лагранжа: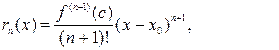
 если
если  и
и  если
если  .
. и рассмотрим вспомогательную функцию
и рассмотрим вспомогательную функцию .
.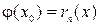 , а
, а  .
. , дифференцируема на
, дифференцируема на 
 и отрезку [x0;x]:
и отрезку [x0;x]: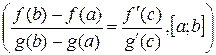


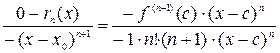
 Þ
Þ  .
. остаточный член формулы Тейлора может быть представлен в виде или в форме Коши:
остаточный член формулы Тейлора может быть представлен в виде или в форме Коши:


 дифференцируема на
дифференцируема на  и ее производная имеет вид
и ее производная имеет вид
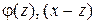 и отрезку [ x 0 ;x ]:
и отрезку [ x 0 ;x ]:

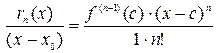 Þ
Þ  .
. ,
, .
. , поэтому
, поэтому

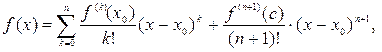
 , если
, если  , если
, если  .
.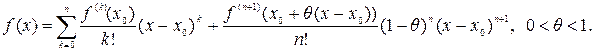
 , формулы Тейлора становятся формулами Маклорена соответственно:
, формулы Тейлора становятся формулами Маклорена соответственно:

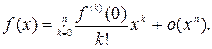
 ,
, при
при 
 , то
, то
 , при
, при 
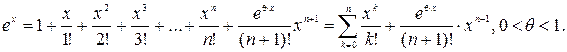

 .
.


