
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дифференциал сложной функции
1. Пусть у = f [ φ (t)] есть сложная функция от t, т.е. у = f (x), где х = φ (t). 2. Тогда ее дифференциал в случае существования производных у ′х и х ′t запишется в виде: dу = y ′t∙ dt, где y ′t = y ′х∙ х ′t так как у = f [ φ (t)]. 3. Тогда dу = y ′х∙ х ′t∙ dt = y ′х∙ dx = f ′x∙ dx. 4. Итак, получили, что формула dу = f ′(х)∙ dx верна как в случае, когда х – независимая переменная, так и в случае, когда х – функция от малой переменной t. 5. В первом случае под dx понимается дифференциал независимой переменной (dx = ∆x), а во втором случае – дифференциал функции (dx ≠ ∆x). Поэтому формула дифференциала dу = f ′(х)∙ dx носит название инвариантной (неизменной) формы дифференциала. А формула dу = f ′(х)∙ ∆x свойством инвариантности не обладает [4]. Пример. у = tg x, dy -? Если х = t 2, то dy = sec2 xdx = sec2 х 2 tdt = 2t sec2 t2· dt, так как dx = 2·t· dt [4]. Дифференциалы высших порядков Определение 17 Дифференциал от дифференциала функции у = f (x) в некоторой точке x 0 называется дифференциалом второго порядка в этой точке и обозначается: d (dy) = d 2 y = d (f ′(x 0) dx) = f ′′(x 0) dx 2. Определение 18 Дифференциал от дифференциала второго порядка называется дифференциалом третьего порядка и обозначается d 3 y. Определение 19 Дифференциал от дифференциала (n -1) порядка называется дифференциалом n ого порядка и обозначается: dny. Замечание При этом дифференциал независимой переменной рассматривается всё время как постоянная. Из определения дифференциалов высшего порядка следует их способ вычисления. Пусть функция у = f (x) имеет в точке х производные любого порядка (х – независимая переменная): dу = y ′∙ dx. Тогда d 2 y = d (dy) = (y ′∙ dx)′ dx = y ″ dx dx = y ″ dx 2; d 3 y = d (d 2 y) = (y ″ dx 2)′ dx = y″′ dx 2 dx = y ″′ dx 3; ……………………………………………….; dny = d (dn -1 y) = (y (n -1)∙ dxn -1)′ dx = y (n)∙ dxn -1 dx = y (n)∙ dxn. Из этих выражений следует, что для любого n: dny = y ( n )∙ dxn, следовательно ч.т.д. Теорема Как для производных, так и для дифференциалов высшего порядка справедлива следующая формула: dn (c ∙ U) = c dn U; dn (U dn (U ∙ V) = dnU ∙ V + n ∙ dn -1 UdV + Замечание Формула dny = y ( n )∙ dxn не обладает свойством инвариантности [4]. Модуль Тема №7
Основные теоремы дифференциального исчисления и их приложение к исследованию функций Лекция №5 1. Теорема Ферма. 2. Геометрическая интерпретация теоремы Ферма. 3. Теорема Ролля. 4. Геометрическая интерпретация теоремы Ролля. 5. Теорема Лагранжа. 6. Геометрический смысл теоремы Лагранжа. 7. Следствия к теореме Лагранжа. 8. Теорема Коши. Теорема Ферма Пьер Ферма (1601-1665) – французский математик
Теорема. Пусть функция Доказательство 1. Пусть функция 2. Тогда для любой точки 3. Если 4. Если 5. Тогда если в точке 6. Известно, что производная в точке существует тогда и только тогда, когда левая и правая производные равны между собой и равны производной в точке. Значит, должны существовать правая и левая производные функции в точке a) б) 7. Но ч.т.д.
|
|||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 966; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.137.218 (0.007 с.) |
 .
. [4].
[4]. V) = dnU
V) = dnU 
 определена в некоторой окрестности точки
определена в некоторой окрестности точки  и принимает в ней наибольшее или наименьшее значение. Тогда если в точке
и принимает в ней наибольшее или наименьшее значение. Тогда если в точке  , то она равна нулю, т.е.
, то она равна нулю, т.е.  .
. , и для определенности принимает в точке
, и для определенности принимает в точке  выполняется неравенство:
выполняется неравенство:  .
. , то дробь
, то дробь  . (1)
. (1) , то дробь
, то дробь  . (2)
. (2) .
.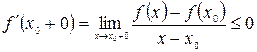 ;
; .
. , только тогда будут равны производные.
, только тогда будут равны производные.


