
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ограниченные сверху, снизу и ограниченные функцииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Определение №1. Функция Определение №2. Функция Определение №3. Функция Очевидно, что функция Верхняя и нижняя грани функции Определение №1. Верхняя грань множества значений Определение №2. Нижняя грань множества значений Замечание. 1. Верхняя (нижняя) грань функции может быть как конечной, так и бесконечной. 2. Функция ограничена сверху (снизу) на множестве Наибольшие, наименьшие, максимальные, минимальные и экстремальные значения функции Определение №1. Функция Определение №2. Наибольшие (наименьшие) значения функции называется также максимальным (минимальным) значением и пишется: Определение №3.
График функции Определение №1. График функции – это множество пар точек Определение №2. Соотношение Пример: График функции
Рис.1.Рис.2. Замечание. Не всякая линия является графиком какой-либо одной функции. Пример. Уравнение окружности А это противоречит требованию однозначности в определении функций. Но часть окружности, лежащая в нижней полуплоскости, является графиком функции
Способы задания функции Определение. Задать функцию Существует три способа задания функции: аналитический, табличный и графический. I. Аналитический явный способ задания функции Сущность способа: Зависимость между переменными величинами определяется с помощью формулы. Она указывает, какие действия надо выполнить, чтобы получить значение функции, соответствующие данному значению аргумента. Пример: Формула
Рис.3. Данная функция задана с помощью нескольких формул. Эта функция определена на всей числовой прямой. А множество ее значений состоит из –1;0;1. 2. Функция Дирихле определена на всей числовой прямой. А множество ее значений состоит из двух чисел: 1,0. Функцию Дирихле графически изобразить нельзя. II. Аналитически неявный способ задания функции 1. Неявные функции Определение. Пусть задано уравнение вида Замечание. 1. Термин «неявная» отражает не характер функциональной зависимости, а лишь способ ее задания. 2. Одна и та же функция может быть задана как явно, так и неявно. Пример: Функции, заданные явно 3. Сложные функции Если заданы функции Определение. Функция, определяемая соотношением
Сложная функция отражает не характер функциональной зависимости, а лишь способ ее задания. Пример. III. Табличный способ задания функции Пусть дана таблица
Поставим в соответствие каждому значению Пример: Таблицы тригонометрических функций; таблицы логарифмов и т.д. IV. Графический способ задания функции Соответствие между переменными
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 3540; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |

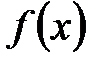 , определенная на некотором множестве
, определенная на некотором множестве 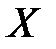 , называется ограниченной сверху на этом множестве, если существует такое число
, называется ограниченной сверху на этом множестве, если существует такое число 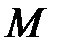 , что для любого
, что для любого 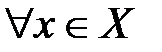 выполняется неравенство:
выполняется неравенство: 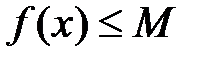 .
.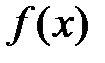 , определенная на некотором множестве
, определенная на некотором множестве 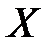 , называется ограниченной снизу на этом множестве, если существует такое число
, называется ограниченной снизу на этом множестве, если существует такое число 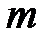 , что для любого
, что для любого 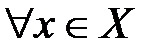 выполняется неравенство
выполняется неравенство 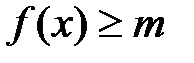 .
. , ограниченная сверху и снизу на множестве
, ограниченная сверху и снизу на множестве  ограничена на множестве
ограничена на множестве 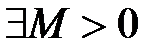 , что для любого
, что для любого 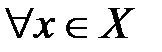 выполняется неравенство
выполняется неравенство 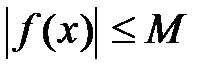 или
или 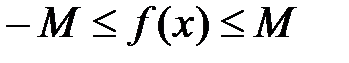 .
. числовой функции
числовой функции 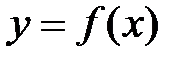 , определенной на множестве
, определенной на множестве 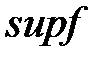 или
или 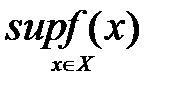 .
.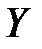 числовой функции
числовой функции 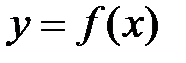 , определенной на множестве
, определенной на множестве 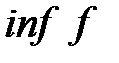 или
или 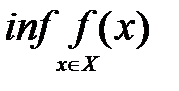 .
.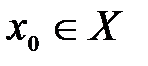 наибольшие (наименьшие) значения, если
наибольшие (наименьшие) значения, если 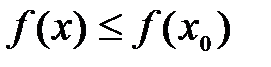
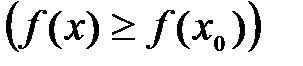
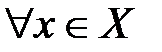 .
.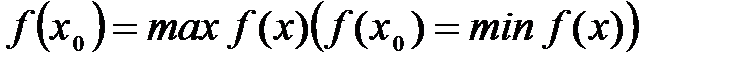 или
или 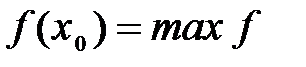
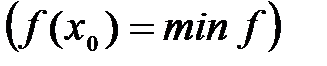 .
.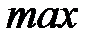 и
и 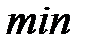 значения функции называются экстремальными.
значения функции называются экстремальными.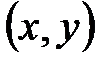 , координаты которых связаны соотношением
, координаты которых связаны соотношением 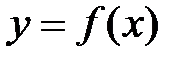 .
.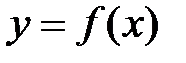 называется уравнением графика функции.
называется уравнением графика функции.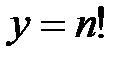 состоит из отдельных точек (рис.1.).
состоит из отдельных точек (рис.1.).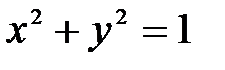 не является графиком одной функции, так как каждое
не является графиком одной функции, так как каждое  входит не в одну, а в две пары чисел
входит не в одну, а в две пары чисел 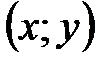 этого множества
этого множества 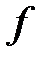 .
. 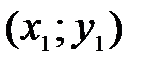 и
и 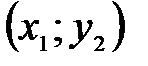 , где
, где 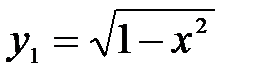 ;
; 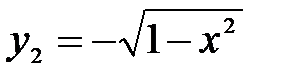 .
.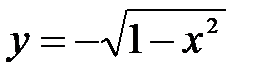 . А другая часть окружности, лежащая в верхней полуплоскости, является графиком функции
. А другая часть окружности, лежащая в верхней полуплоскости, является графиком функции 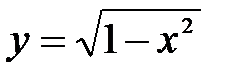 .
.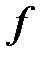 – это значит, указать, как по каждому значению аргумента
– это значит, указать, как по каждому значению аргумента 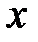 найти соответствующие ему значения функции
найти соответствующие ему значения функции 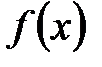 .
.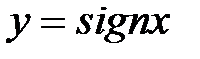 (сигнум с латинского языка «знак») задает функцию
(сигнум с латинского языка «знак») задает функцию 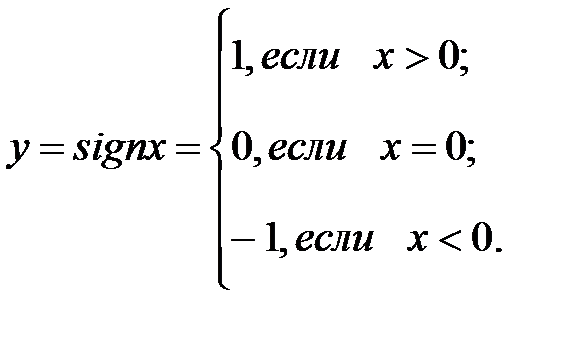
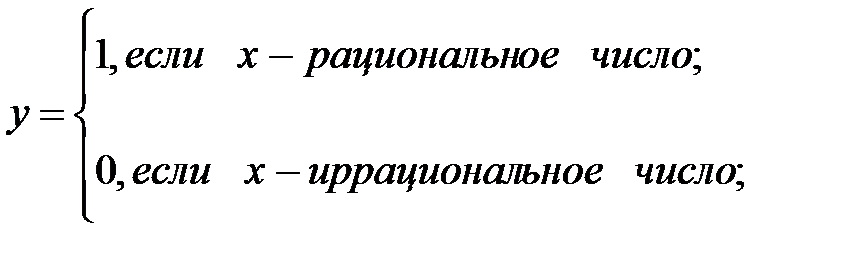
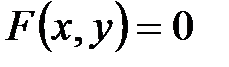 , т.е. задана функция двух действительных переменных
, т.е. задана функция двух действительных переменных 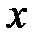 и
и 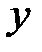 . Причем, рассматриваются только такие пары (если они существуют), для которых выполняется условие
. Причем, рассматриваются только такие пары (если они существуют), для которых выполняется условие 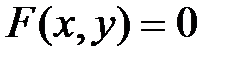 . Функции, задаваемые таким образом, называются неявными.
. Функции, задаваемые таким образом, называются неявными.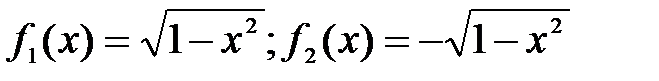 могут быть заданы и неявным образом с помощью уравнения:
могут быть заданы и неявным образом с помощью уравнения:  .
.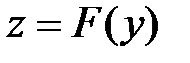 и
и 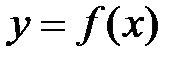 , причем, область определения функции
, причем, область определения функции 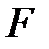 содержит множество значений функции
содержит множество значений функции 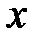 из области определения функции
из области определения функции 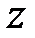 такое, что
такое, что 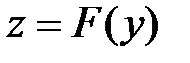 , где
, где 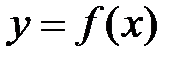 .
.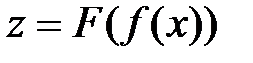 называется сложной функцией или, композицией функций или суперпозицией функций
называется сложной функцией или, композицией функций или суперпозицией функций 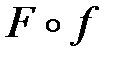 т.е.
т.е.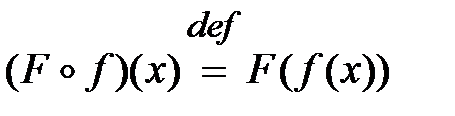 .
.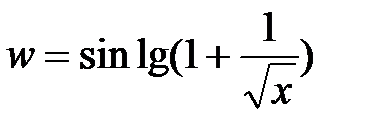 . Данную функцию можно рассматривать как суперпозицию следующих функций:
. Данную функцию можно рассматривать как суперпозицию следующих функций: 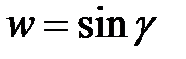 ;
; 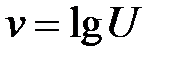 ;
; 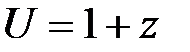 ;
; 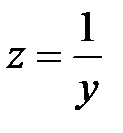 ;
; 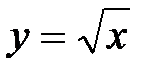 .
.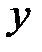 , стоящее во второй строке под числом
, стоящее во второй строке под числом 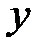 , перечисленных во второй строке. С помощью таблицы можно задать функцию только при конечном числе значений аргумента. Таблицы часто используются для задания функции.
, перечисленных во второй строке. С помощью таблицы можно задать функцию только при конечном числе значений аргумента. Таблицы часто используются для задания функции.


