
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Практическое занятие № 8. Производная и дифференциал.
Задания АЗ 6.1: [14], часть 1, №№ 1,2, АЗ 6.2: [14], часть 1, №№ 1-3, АЗ 6.3: [14], часть 1, №№ 1-3 АЗ 6.4: [14],часть 1, №№ 1-3. Методические рекомендации. При нахождении производной функции необходимо применять правила дифференцирования и таблицу производных. Сложную функцию следует дифференцировать, разложив на элементарные, обратную по формуле Пример 1. Найти производную функции Решение: Полагая Пример 2. Найти производную Решение.Преобразуем функцию Тогда Пример 4. Найти дифференциал второго порядка функции Решение: Имеем
Осн. лит. 14, часть 1, [189-201] Доп. лит. 29,[272-275]. Контрольные вопросы: 1. Как найти производную функции заданной параметрически? 2. В чем заключается геометрический и механический смысл производной первого порядка? 3. Сформулируйте алгоритм метода логарифмического дифференцирования.
Практическое занятие № 9. Исследование поведения функций и их графиков. Приложения дифференциального исчисления к геометрии. Задания. АЗ - 6.7 [14], часть 1, №№ 1-5, АЗ - 6.8 [14], часть 1, №№ 1. Методические рекомендации. Для полного исследования поведения функции необходимо определить точки экстремума и точки перегиба графика данной функции с помощью производных. А для определения основных свойств функции нужно применить материал изложенный в Лекции 8. С помощью теории пределов находятся асимптоты и возможные точки разрыва графика функции. Пример 1. Найти интервалы возрастания и убывания функции Решение.Найдем производную Пример 2. Найти точки перегиба кривой Решение. Находим Определим знак Следовательно, точка Пример 3. Найти асимптоты кривой Решение.Функция определена в интервалах
Итак, наклонные асимптоты: Осн. лит. 14, часть 1, [202-214] Доп. лит. 29, [ 277-279]. Контрольные вопросы: 1. Как используется правило Лопиталя для устранения неопределенностей вида 2. Как определяются интервалы монотонности и выпуклости графика функции? 3. Чему равен угловой коэффициент наклонной асимптоты? Практическое занятие № 10. Неопределенный интеграл. Свойства неопределенного интеграла. Таблица основных интегралов. Метод подстановки. Интегрирование по частям. Задания: А3 – 8.1 [14], часть 1, № 1-8, А3 – 8.2 [14], часть 1, № 1-8, А3 – 8.4 [14], часть 1, № 1-4. А3 – 8.5 [14], часть 1, № 1-3. Методические рекомендации. При нахождении неопределенных интегралов используются их свойства и таблица интегралов. Для приведения заданного интеграла к табличному применяется методы подведения под знак дифференциала и метод подстановки. При использовании метода интегрирования по частям нужно правильно представить подынтегральное выражение в виде произведения двух сомножителей Пример 1. Вычислить интеграл Решение. Представляя интеграл алгебраической суммы в виде суммы интегралов, вынося постоянные множители за знаки интегралов и применяя формулы 1,2 таблицы основных интегралов, получим
Пример 2. Найти интеграл Решение. Полагаем
Пример 3. Найти интеграл Решение. Полагаем Тогда Полагаем Применяя формулу интегрирования по частям, получим:
Осн. лит.: 14, часть 2, [15-34] Доп. лит.: 29,[297-301]. Контрольные вопросы: 1. Как правильно представить подынтегральное выражение в виде произведения двух сомножителей 2. Как внести множитель под знак дифференциала? 3. Как выделить целую часть у неправильной дроби подынтегральной функции?
|
|||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 368; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.19.30.232 (0.01 с.) |
 и т.д. Производная n-го порядка определяется дифференцированием производной n-1 го порядка. Согласно определению дифференциала можно найти дифференциала любого порядка.
и т.д. Производная n-го порядка определяется дифференцированием производной n-1 го порядка. Согласно определению дифференциала можно найти дифференциала любого порядка. .
. и
и 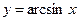 , имеем
, имеем  и
и  . Отсюда получаем
. Отсюда получаем  .
.
 .
.
 .
. .
. ,
,  . Тогда
. Тогда  .
.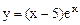 . Исследовать функцию на экстремум.
. Исследовать функцию на экстремум. и стационарные точки, решая уравнения
и стационарные точки, решая уравнения  . Определим знак производной
. Определим знак производной  в окрестности точки
в окрестности точки  :
:  , при
, при  и
и 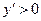 при
при  . Следовательно, в точке
. Следовательно, в точке  функция имеет минимум
функция имеет минимум  . Функция возрастает на интервале
. Функция возрастает на интервале  ; убывает на интервале
; убывает на интервале  .
. .
. ,
,  . Критическая точка второго рода:
. Критическая точка второго рода:  .
. в окрестности
в окрестности  , т.е. (5,2) – точка перегиба.
, т.е. (5,2) – точка перегиба. .
. . Имеем
. Имеем  , следовательно
, следовательно 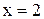 - вертикальная асимптота. Горизонтальных асимптот нет, так как предел
- вертикальная асимптота. Горизонтальных асимптот нет, так как предел 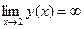 не является конечной величиной. Находим:
не является конечной величиной. Находим:
 .
.
 .
. , т.е.
, т.е.  .
. ,
,  и
и  ?
? и
и 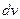 .
. .
. Здесь и далее произвольные постоянные, входящие в каждый из складываемых неопределенных интегралов, объединяются в одну произвольную постоянную.
Здесь и далее произвольные постоянные, входящие в каждый из складываемых неопределенных интегралов, объединяются в одну произвольную постоянную. .
. , внесем функцию
, внесем функцию  под знак дифференциала, получим:
под знак дифференциала, получим: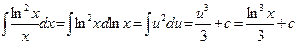 .
. .
.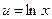 ,
,  , тогда
, тогда  .
. .
. , так как достаточно иметь какую – либо одну первообразную. Итак,
, так как достаточно иметь какую – либо одну первообразную. Итак,  .
.
 .
.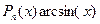 ?
?


