
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Решение уравнения колебания струны методом Даламбера.
Одним из широко используемых способов решения уравнений колебание струны является метод характеристик, называемый методом Даламбера. В основе его лежит тот, факт, что с помощью замены
уравнение
Преобразуется в уравнение
где Для определиний функций
Это общее решение (решение Даламбера). Здесь Рассмотрим задачу Коши для бесконечной струны: найти функцию
По заданным начальным условиям
Определяются функции Φ и Т, и искомое решение имеет вид
Формула (3) называется формулой Даламбера. Эта формула доказывает единственность решения задачи Коши. В частности, когда начальная скорость равна нулю (
Откуда легко вычислить отклонение струны от положения равновесия для любой из её точек; оно равно сумме левой и правой бегущих волн, причем начальная форма каждой волны определяется функцией В случае полубесконечной струны, кроме
для закрепленной в точке х=0 струны,
для свободного конца в точке х=0,
для упругого закрепления в точке х=0. В случае однородных граничных условий (4) и (5) решение задачи о колебании полубесконечной струны сводиться к решению задачи о колебании бесконечной струны путем продолжении начальных условий на всю ось нечетным образом для условия (4), то есть полагают Задача. Найти форму достаточно длинной струны, определяемой уравнением a) b) c) Решение: а) Полагая в формуле Даламбера
откуда определяем форму кривой в указанном моменте времени
б)
В момент времени в) По условию
Примеры: 1. Найти решение уравнения 2. Найти решение уравнения 1) 2) 3) 3. Найти форму струны в момент времени 1) 2) 3)
4. Найти решение уравнения
Лекция 10
|
|||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 2694; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.240.224 (0.01 с.) |
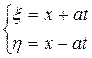
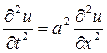 (1)
(1) , которое имеет общее решение
, которое имеет общее решение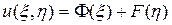 ,
,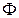 и F - произвольные дважды дифференцируемые функции.
и F - произвольные дважды дифференцируемые функции.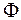 и F, то есть для определения закона колебаний струны, требуется использовать начальные условия, а для некоторых задач и граничные. Если вернуться к старым переменнам x и t, то общее решение примет вид
и F, то есть для определения закона колебаний струны, требуется использовать начальные условия, а для некоторых задач и граничные. Если вернуться к старым переменнам x и t, то общее решение примет вид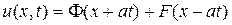
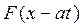 характеризует прямую волну (кривая F(x) смещается вправо со скоростью а), а
характеризует прямую волну (кривая F(x) смещается вправо со скоростью а), а  - обратную волну (кривая Φ(х) смещается влево со скоростью а).
- обратную волну (кривая Φ(х) смещается влево со скоростью а).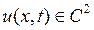 , удовлетворяющую уравнению
, удовлетворяющую уравнению
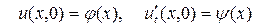 (2)
(2)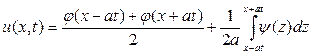 (3)
(3) ), то
), то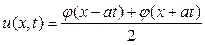
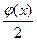 , равной половине начального отклонения.
, равной половине начального отклонения. , необходимо добавить еще граничные условия (конец предполагается в точке х=0).
, необходимо добавить еще граничные условия (конец предполагается в точке х=0).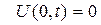 (4)
(4)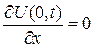 (5)
(5)
 и четным образом для условия (5), то есть
и четным образом для условия (5), то есть  .
.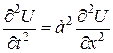 в момент времени
в момент времени 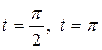 , если заданы начальные смещение и скорости:
, если заданы начальные смещение и скорости:
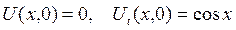

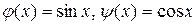 , найдем смещение
, найдем смещение 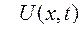 в любой точке и в любой момент t
в любой точке и в любой момент t
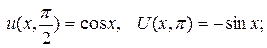

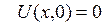 при
при 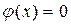 колебательный процесс будет описан по формуле
колебательный процесс будет описан по формуле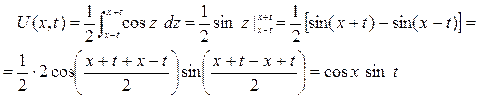
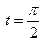 струна имеет форму косинусоида:
струна имеет форму косинусоида: 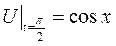 а момент
а момент 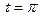 она совпадает с осью абсцисс
она совпадает с осью абсцисс  .
.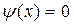 , тогда имеем
, тогда имеем Форма струны в указанном моменте времени определяется уравнением
Форма струны в указанном моменте времени определяется уравнением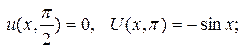
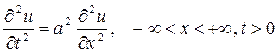 , удовлетворяющее начальным условиям
, удовлетворяющее начальным условиям  ,
, 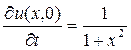 .
. и
и 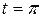 , если
, если ,
, 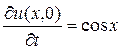
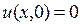 ,
, 
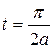 , определяемую уравнением
, определяемую уравнением 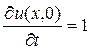
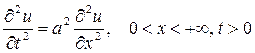 , удовлетворяющее начальным условиям
, удовлетворяющее начальным условиям 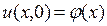 ,
, 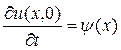 и граничными условиями
и граничными условиями 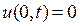 .
.


