
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дифференциальные уравнения первого порядка, разрешенные относительно производной. Общие сведенияСтр 1 из 4Следующая ⇒
ВАРИАНТЫ
15. Бегунов М. 16. Горбачева В. 17. Евсикова А. 18. Заикин А. 19. Камсулина М. 20. Марченкова О. 21. Маюрова Г. 22. Прадед А. 23. Шумакова М. 24. Юрасова А.
Замечание: теория и примеры – в помощь. Решаем то, где написано: ЗАДАНИЯ ПО ВАРИАНТАМ:
ЗАДАЧИ № 1-7
Задачи № 1-№ 5. Уравнения первого порядка: с разделяющимися переменными и приводящиеся к ним, однородные и приводящиеся к однородным, линейным уравнения, уравнение Бернулли, уравнение в полных дифференциалах. Задача № 6. Смешанные задачи на д.у. первого порядка. Определить тип уравнения и указать в общем виде метод решения. Задача № 7. Смешанные задачи на д.у. первого порядка. Определить тип уравнения и решить.
Задача № 1. Уравнения с разделяющимися переменными и приводящиеся к ним. Дифференциальное уравнение
Уравнение Путем деления на произведение
Общий интеграл этого уравнения имеет вид
Замечание. Деление на Дифференциальное уравнение
где уравнение с разделяющимися переменными. Пример 1. Решить уравнение Решение. Разделим обе части уравнения на произведение
Получим уравнение с разделенными переменными. Интегрируя его, найдем
После потенцирования получим
Откуда Обозначая Получили общий интеграл этого уравнения. Функции Ответ: Пример 2. Найти частное решение уравнения Решение. Имеем Разделяем переменные, для этого обе части уравнения делим на произведение
Интегрируя, найдем общий интеграл
в качестве производной константы После потенцирования, получим Найдем константу
Искомое частное решение или решение задачи Коши
Ответ: Упражнения. Решить уравнения 1. 2. 3. 4. ЗАДАНИЯ ПО ВАРИАНТАМ: Решить уравнения с разделяющимися переменными:
Пример 3. Решить уравнение Решение. Запишем уравнение в виде Разделяя переменные, будем иметь Отсюда интегрированием находим
Ответ: Упражнения. Решить уравнения 1. 2. 3. 4.
ЗАДАНИЯ ПО ВАРИАНТАМ: Решить однородные дифференциальные уравнения:
Пример 4. Решить уравнение Решение. Вид уравнения нормальный
Ответ:
Упражнения. Решить уравнения 1. 2. Приводим к виду 3. 4.
Уравнение линейное относительно функции
ЗАДАНИЯ ПО ВАРИАНТАМ: Решить линейные дифференциальные уравнения первого порядка:
Пример 5. Решить уравнение Бернулли Приведем уравнение к виду
Обе части уравнения умножим на
Получили Поэтому Ответ: Упражнения. Решить уравнения 1. 2. 3. Уравнение следует переписать в виде
4. Обе части уравнения следует умножить на
ЗАДАНИЯ ПО ВАРИАНТАМ: Решить уравнения Бернулли:
Пример 6. Решить уравнение Решение. Проверим является ли данное уравнение уравнением в полных дифференциалах
Получили, что Найдем функцию
Из первого уравнения, интегрированием по
где Частная производная
Отсюда
Ответ:
Упражнения. Решить уравнения 1. 2. 3. 4.
ЗАДАНИЯ ПО ВАРИАНТАМ: Проинтегрировать уравнения в полных дифференциалах:
ВАРИАНТЫ
15. Бегунов М. 16. Горбачева В. 17. Евсикова А. 18. Заикин А. 19. Камсулина М. 20. Марченкова О. 21. Маюрова Г. 22. Прадед А. 23. Шумакова М. 24. Юрасова А.
Замечание: теория и примеры – в помощь. Решаем то, где написано: ЗАДАНИЯ ПО ВАРИАНТАМ:
ЗАДАЧИ № 1-7
Задачи № 1-№ 5. Уравнения первого порядка: с разделяющимися переменными и приводящиеся к ним, однородные и приводящиеся к однородным, линейным уравнения, уравнение Бернулли, уравнение в полных дифференциалах. Задача № 6. Смешанные задачи на д.у. первого порядка. Определить тип уравнения и указать в общем виде метод решения. Задача № 7. Смешанные задачи на д.у. первого порядка. Определить тип уравнения и решить.
Дифференциальные уравнения первого порядка, разрешенные относительно производной. Общие сведения
Д.У. первого порядка это равенство, содержащее неизвестную функцию
Обычно уравнение (1) стараются представить в форме, разрешенной относительно производной:
или в форме, содержащей дифференциалы:
От формы (2) можно перейти к форме (3) и наоборот. В самом деле, если в уравнении (2) заменить
Что представляет собой форму (3), где Наоборот, член уравнения (3) вправо и разделить обе части уравнения на Таким образом, Формы (2) и (3) совершенно равноправны, в дальнейшем используется та или другая форма. Еще раз подчеркнем, что для того, чтобы от формы (2), перейти к форме (3) надо Чтобы от формы (3) перейти к форме (2), из равенства (3) надо выразить отношение (частное) Дифференциальному уравнению удовлетворяет, вообще говоря, целая система функций. Для выделения одной из них следует указать ее значение при каком-либо значении аргумента
Решение уравнения (2) с условием (4) называют еще задачей Коши. Решение.
Практически для определения С следует подставить в общее решение (общий интеграл) вместо
Относительно произвольного С. Пусть Перейдем к рассмотрению отдельных типов дифференциальных уравнений, нахождение общих решений (общих интегралов) которых сводится к выполнению обычных операций вычисления интегралов. В задачах № 1 - № 5 найти общее решение
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 289; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.156.140 (0.158 с.) |
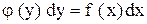 называется уравнением с разделенными переменными, его общий интеграл имеет вид
называется уравнением с разделенными переменными, его общий интеграл имеет вид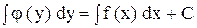 .
. , в котором коэффициенты при дифференциалах распадаются на множители, зависящие только от
, в котором коэффициенты при дифференциалах распадаются на множители, зависящие только от  и только от
и только от 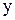 называется уравнением с разделяющимися переменными.
называется уравнением с разделяющимися переменными.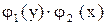 оно приводится к уравнению с разделенными переменными:
оно приводится к уравнению с разделенными переменными: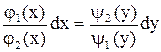 .
.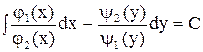 .
.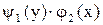 может привести к потере частных решений, обращающих в ноль произведение
может привести к потере частных решений, обращающих в ноль произведение 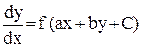 ,
,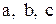 - постоянные, заменой переменных
- постоянные, заменой переменных 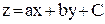 преобразуется в
преобразуется в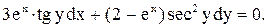

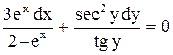 .
.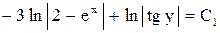 .
.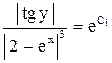 или
или 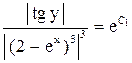 .
.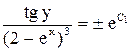 .
.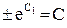 , будем иметь
, будем иметь 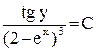 или
или 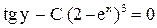 .
.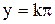 ,
, 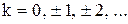 и
и  - являются частными решениями.
- являются частными решениями.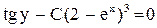 - общий интеграл.
- общий интеграл.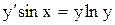 , удовлетворяющее начальному условию
, удовлетворяющее начальному условию 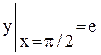 .
.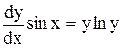 или
или 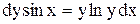 .
.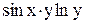
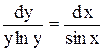 .
.
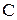 взяли
взяли 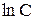 .
.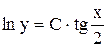 или
или 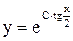 - общее решение исходного уравнения.
- общее решение исходного уравнения. ,
,  или
или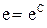 отсюда
отсюда  .
.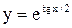 .
.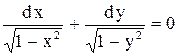 . Ответ:
. Ответ: 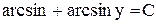 .
.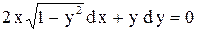 . Ответ:
. Ответ:  .
.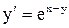 . Ответ:
. Ответ: 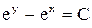 .
.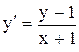 . Ответ:
. Ответ: 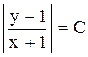 или
или 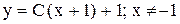 .
.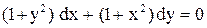 .
.
 .
.
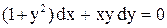 .
.
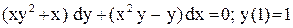 .
.
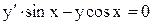 .
.
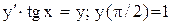 .
.
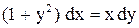 .
.
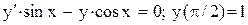 .
.
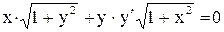 .
.
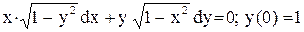 .
.
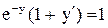 .
.
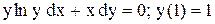 .
.
 .
.
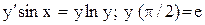 .
.
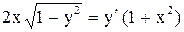 .
.
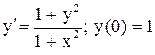 .
.
 .
.
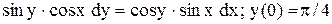 .
.
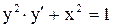 .
.
 .
.
 .
.
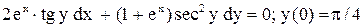 .
.
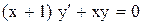 .
.
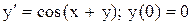 .
.
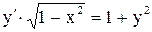 .
.
 .
.
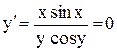 .
.
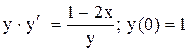 .
.
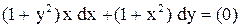 .
.
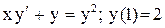 .
.
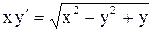 .
. , разделив на
, разделив на 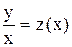 . Тогда
. Тогда 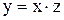 ,
,  . Получим
. Получим 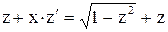 или
или  .
.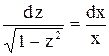 .
.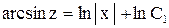
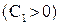 или
или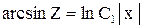 , так как
, так как 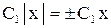 , то обозначая
, то обозначая 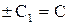 , получим
, получим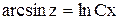 . Заменяя
. Заменяя 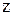 на
на 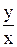 , будем иметь общий интеграл
, будем иметь общий интеграл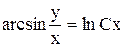 , отсюда
, отсюда 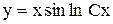 - общее решение.
- общее решение.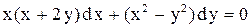 . Ответ:
. Ответ: 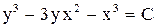 .
.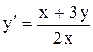 . Ответ:
. Ответ: 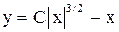 .
.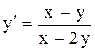 . Ответ:
. Ответ: 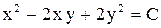 .
.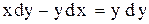 . Соберем коэффициенты при
. Соберем коэффициенты при 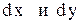
 . Ответ:
. Ответ: 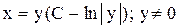 .
.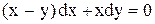 .
.
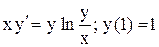 .
.
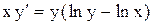 .
.
 .
.
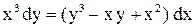 .
.
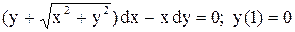 .
.
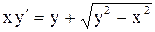 .
.
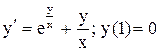 .
.
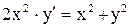 .
.
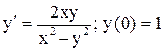 .
.
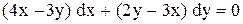 .
.
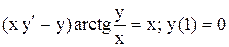 .
.
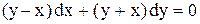 .
.
 .
.
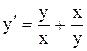 .
.
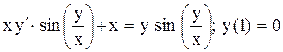 .
.
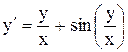 .
.
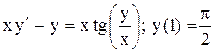 .
.
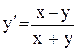 .
.
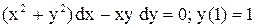 .
.
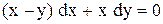 .
.
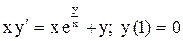 .
.
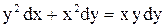 .
.
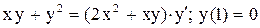 .
.
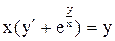 .
.
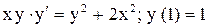 .
.
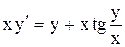 .
.
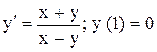 .
.
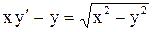 .
.
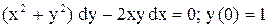 .
.
 .
.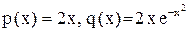 .
.
 .
.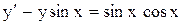 . Ответ:
. Ответ: 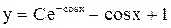 .
.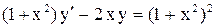 .
.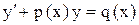 ,
,  и решаем по формуле
и решаем по формуле  . Ответ:
. Ответ: 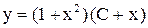 .
.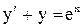 . Ответ:
. Ответ: 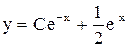 .
. . Ответ:
. Ответ: 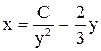 .
.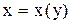 . Приводим его к виду
. Приводим его к виду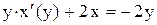 или
или  .
.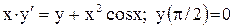 .
.
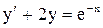 .
.
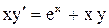 ;
; 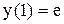 .
.
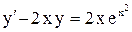 .
.
 .
.
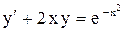 .
.
 .
.
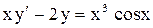 .
.
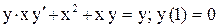 .
.
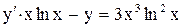 .
.
 .
.
 .
.
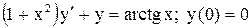 .
.
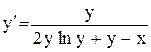 .
.
 .
.
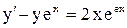 .
.
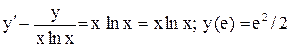 .
.
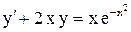 .
.
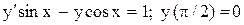 .
.
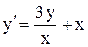 .
.
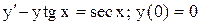 .
.
 .
.
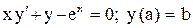 .
.
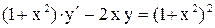 .
.
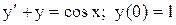 .
.
 .
.
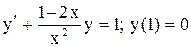 .
.
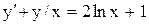 .
.
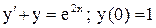 .
.
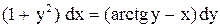 .
.
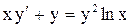 .
.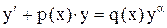
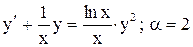 .
.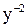 и сделаем замену
и сделаем замену 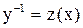 , причем,
, причем, 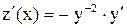 , получим
, получим  - это линейное уравнение относительно
- это линейное уравнение относительно 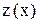 .
.
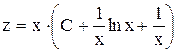 .
. .
.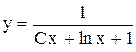 .
. . Ответ:
. Ответ: 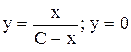 .
.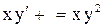 . Ответ:
. Ответ:  .
.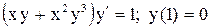 . Ответ:
. Ответ: 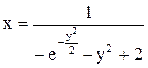 .
.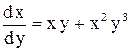 или
или 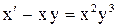 - это уравнение Бернулли относительно функции
- это уравнение Бернулли относительно функции 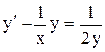 . Ответ:
. Ответ: 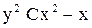 .
. .
. .
.
 .
.
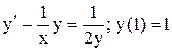 .
.
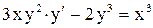 .
.
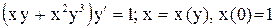 .
.
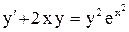 .
.
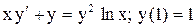 .
.
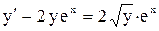 .
.
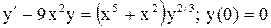 .
.
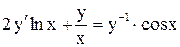 .
.
 .
.
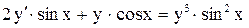 .
.
 .
.
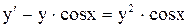 .
.
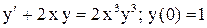 .
.
 .
.
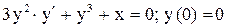 .
.
 .
.
 .
.
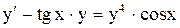 .
.
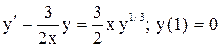 .
.
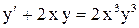 .
.
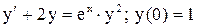 .
.
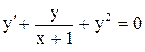 .
.
 .
.
 .
.
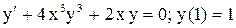 .
.
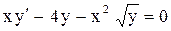 .
.
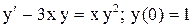 .
.
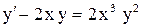 .
.
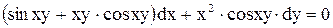 .
.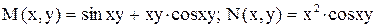 .
.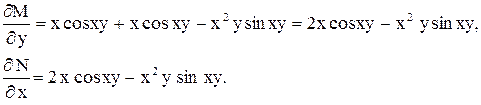
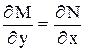 , условие (2) выполнено, значит данное уравнение в полных дифференциалах.
, условие (2) выполнено, значит данное уравнение в полных дифференциалах.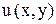 . Для этого имеем систему:
. Для этого имеем систему:
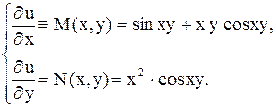
 ,
,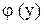 - произвольная функция (вместо постоянной интегрирования С берем функцию
- произвольная функция (вместо постоянной интегрирования С берем функцию  , найденной функции
, найденной функции 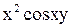 , что дает
, что дает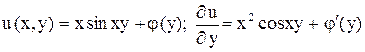 ,
, .
.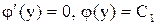 ,
,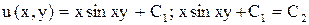 - общий интеграл.
- общий интеграл. , где
, где 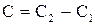 .
.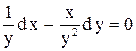 . Ответ:
. Ответ: 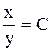 .
. . Ответ:
. Ответ: 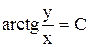 .
.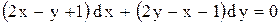 . Ответ:
. Ответ: 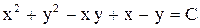 .
. . Ответ:
. Ответ:  .
.
 ,
, уравнение в полных дифференциалах.
уравнение в полных дифференциалах.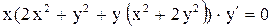 .
.
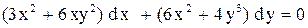 .
.
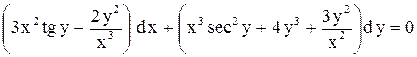 .
.
 .
.
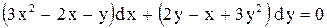 .
.
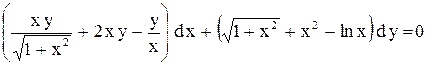 .
.
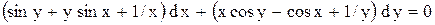 .
.
 .
.
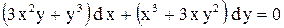 .
.
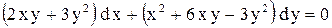 .
.
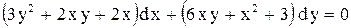 .
.
 .
.
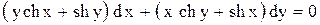 .
.
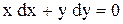 .
.
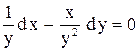 .
.
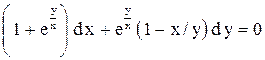 .
.
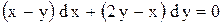 .
.
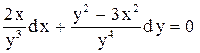 .
.
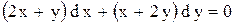 .
.
 .
.
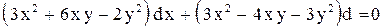 .
.
 .
.
 .
.
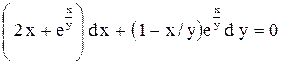 .
.
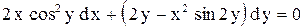 .
.
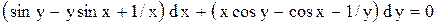 .
.
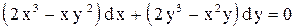 .
.
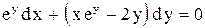 .
.
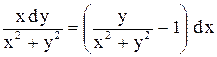 .
.
 .
.
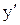 и переменную
и переменную  (1)
(1)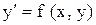 (2)
(2)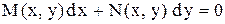 (3)
(3)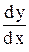 , умножить обе части уравнения на
, умножить обе части уравнения на 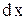 и перенести все члены в одну сторону, то получим
и перенести все члены в одну сторону, то получим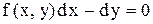 ,
, , а
, а  .
.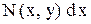 , предполагая, что
, предполагая, что 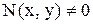 , то получим
, то получим 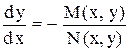 , т.е. форму (2), где
, т.е. форму (2), где 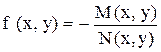 .
.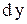 и
и 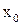 , т.е. задать условие вида
, т.е. задать условие вида 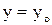 при
при 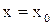 , которое называют начальным условием. Часто его записывают в виде
, которое называют начальным условием. Часто его записывают в виде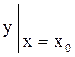
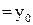 (4)
(4)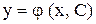 (или интеграл
(или интеграл 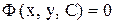 ) д.у. (2), зависящие от произвольного постоянного С, называется общим решением (общим интегралом) д.у. (2), если путем подбора значений произвольного постоянного из него можно получить частное решение (частный интеграл), удовлетворяющее любому возможному начальному условию
) д.у. (2), зависящие от произвольного постоянного С, называется общим решением (общим интегралом) д.у. (2), если путем подбора значений произвольного постоянного из него можно получить частное решение (частный интеграл), удовлетворяющее любому возможному начальному условию  заданные значения
заданные значения 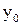 и разрешить уравнение
и разрешить уравнение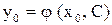
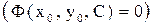
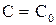 , тогда частное решение будет
, тогда частное решение будет 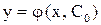 (соответственно частный интеграл
(соответственно частный интеграл 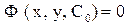 ).
).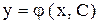 или общий интеграл
или общий интеграл 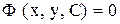 и, где указано, решить задачу Коши.
и, где указано, решить задачу Коши.


