
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теоремы и свойства непрерывных функций. ⇐ ПредыдущаяСтр 4 из 4
Теорема 1: Сумма, произведение и частное двух непрерывных функций есть функция непрерывная (для частного за исключением тех значений аргумента, в которых делитель равен нулю).
Теорема 2: Пусть функции
Теорема 3: Если функция
Всякая элементарная функция непрерывна в каждой точке, в которой она определена. Свойства непрерывных функций: Теорема 1 (Вейерштрасса): Если функция непрерывна на отрезке, то она достигает на этом отрезке своего наибольшего и наименьшего значений. Следствие: Если функция непрерывна на отрезке, то она ограничена на этом отрезке.
Теорема 2(Больцано-Коши): Если функция Следствие: Если функция концах принимает значения разных знаков, то внутри отрезка [а; b] найдется хотя бы одна точка с, в которой данная функция f(x) обращается в нуль:
Четыре условия непрерывности. Точки разрыва и их классификация. 4 условия непрерывности: 1) Определение 1: Функция 1) функция 2) существует 3)
Если в точке x0 нарушено хоть одно из условий, то функция называется разрывной в точке x0 , а точка x0 называется точкой разрыва. 2) Определение 2: Функция 3) Определение 3: Функция 4) Определение 4: Функция
Если в точке x0 нарушено хоть одно из условий, то функция называется разрывной в точке x0 , а точка x0 называется точкой разрыва. Классификация: 1) Существует
2) Не существует
3) Если хотя бы один из односторонних пределов обращается в бесконечность или не существует то точка x0 называется точкой разрыва второго рода.
|
|||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 417; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.131.178 (0.004 с.) |
 непрерывна в точке хо, а функция
непрерывна в точке хо, а функция  непрерывна в точке
непрерывна в точке 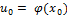 . Тогда сложная функция
. Тогда сложная функция  , состоящая из непрерывных функций, непрерывна в точке x0.
, состоящая из непрерывных функций, непрерывна в точке x0. непрерывна и строго монотонна на [а;b] оси Ох, то обратная функция
непрерывна и строго монотонна на [а;b] оси Ох, то обратная функция так же непрерывна и монотонна на соответствующем отрезке [с;d] оси Оу (без доказательства).
так же непрерывна и монотонна на соответствующем отрезке [с;d] оси Оу (без доказательства).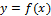 непрерывна на отрезке [a,b] и принимает на его концах неравные значения
непрерывна на отрезке [a,b] и принимает на его концах неравные значения  и
и  , то на этом отрезке она принимает и все промежуточные значения между А и В.
, то на этом отрезке она принимает и все промежуточные значения между А и В. непрерывна на отрезке [а;b] и на его
непрерывна на отрезке [а;b] и на его .
. называется непрерывной в точке x0, если выполняются следующие три условия:
называется непрерывной в точке x0, если выполняются следующие три условия:

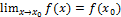
 называется непрерывной в точке x0, если
называется непрерывной в точке x0, если

 , но или
, но или  или
или  , то точка х0 называется точкой устранимого разрыва.
, то точка х0 называется точкой устранимого разрыва. , которые не равны между собой, то точка х0 называется точкой разрыва первого рода, а разность
, которые не равны между собой, то точка х0 называется точкой разрыва первого рода, а разность 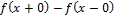 скачком функции
скачком функции 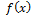 в точке x0.
в точке x0.


