
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Разложение некоторых элементарных функций по формуле маклонена
Формула Тейлора является эффективным средством для вычисления пределов функций, с которыми часто приходится иметь дело при исследовании функций.
Условия возрастания и убывания функций. Точки экстремума. Достаточные условия возрастания и убывания функции в точке и на интервале Теорема. Для того чтобы функция f (x), дифференцируемая в точке х 0 Î (а, b), возрастала (убывала) в точке х 0, достаточно, чтобы f ' (x 0) > 0 (f ' (x 0) < 0).
В достаточно малой окрестности точки х 0 имеем
где sign A означает "знак выражения А". Для случая f ' (x 0) > 0 имеем sign f ' (x 0) = + 1, поэтому sign (f (x 0 + h) − f (x 0)) = sign (h). Откуда следует f (x 0 − h) < f (x 0) < f (x 0 + h), что означает возрастание функции в точке.
Необходимые условия возрастания и убывания функции в точке и на интервале Теорема. Для того чтобы функция f (x), дифференцируемая в точке х 0 Î (а, b), возрастала (убывала) в точке x 0, необходимо, чтобы её производная в точке х 0 была неотрицательной f ' (x0) ≥ 0 (неположительной f ' (x0) ≤ 0). f (x 0 − h) < f (x 0) < f (x 0 + h) В этом случае для положительного приращения h имеем
Выполняя предельный переход в неравенствах, получим
Аналогично
Так как функция имеет производную в точке, то
что и требовалось доказать. f ' (x) > 0, (f ' (x) < 0), то функция f (x) возрастает (убывает) на отрезке [ а, b ]. f (x 2) − f (x 1) = f ' (c)·(x 2 − x 1), где с Î (x 1; x 2). Из этого соотношения следует sign (f (x 2) − f (x 1)) = sign f ' (c) В случае f ' (x) > 0 для всех х Î (а, b) имеем f (x 2) > f (x 1), и большему значению аргумента соответствует большее значение функции. Что свидетельствует о возрастании функции.
Точки экстремума Точка x 0 называется точкой строгого локального максимума (минимума) функции f (x), если для всех значений аргумента из некоторой достаточно малой δ -окрестности точки х 0 выполняется неравенство f (x) < f (x 0) (f (x) > f (x 0)) при х ≠ x 0.
|
|||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 350; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.215.75 (0.005 с.) |
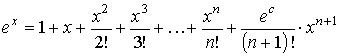 ,
,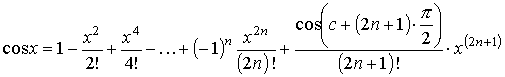 ,
,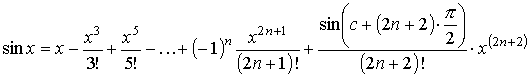 ,
,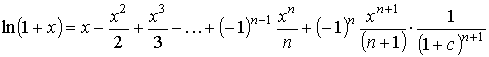 ,
,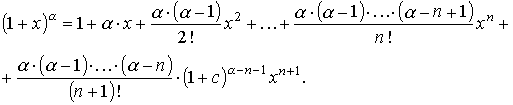
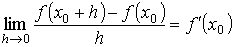 .
.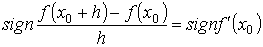 ,
,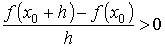 и
и 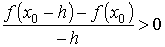 .
.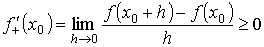 .
.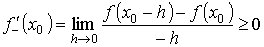 .
.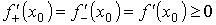 ,
,


