
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Геометрический смысл теоремы Лагранжа
Величина f (x) − f (x 0) ≈ f '(x 0)·(x −x 0). Отличие только лишь в выборе точки для подсчета значения производной и в знаке равенства. Теорема Коши Пусть функции f (x) и g (x) непрерывны на [ a, b ] и дифференцируемы на (a, b). Пусть, кроме того, во всех точках интервала (a, b) функция g (x) имеет ненулевую производную g ' (x) ≠ 0. Тогда существует точка c Î (a, b), такая, что справедлива формула
Д о к а з а т е л ь с т в о. Покажем сначала, что знаменатель левой части формулы не обращается в ноль. Если допустить, что g (b) = g (a), то по теореме Ролля для функции g (x) найдется точка x Î (a, b), в которой g ' (x) = 0. А это противоречит условию, что g ' (x) ≠ 0 на (a, b).
Функция F (x) на [ a, b ] удовлетворяет условиям теоремы Ролля: F(x) непрерывна на [ a, b ], дифференцируема на (a, b), и, кроме того, на концах интервала принимает равные значения F (a) = F (b) = 0. По теореме Ролля для F (x) существует точка c Î (a, b), такая,что F ' (c) = 0. Так как
то
Откуда, учитывая, что g '(c) ≠ 0, следует искомое соотношение.
Правило Лопиталя. Первое правило Лопиталя Пусть функции f (x) и g (x) непрерывны на отрезке [ а, b ] и дифференцируемы на интервале (а, b), и пусть g ' (x) ≠ 0 всюду в (а, b). Пусть, далее, известно, что f (а) = g (а) = 0. Тогда говорят, что отношение
при х → а + 0 представляет собой неопределённость вида
то и
Доказательство. Предположим, что ∞ < A < + ∞. Для заданного как угодно малого числа e > 0 выберем х 0 так, чтобы в интервале (а, x 0) выполнялось неравенство
Применим теорему Коши к отрезку [ а, x 0], Если х
и, следовательно, для всех х
Это означает, что Второе правило Лопиталя Пусть функции f (x) и g (x) непрерывны и дифференцируемы в интервале (a, b) (может быть, бесконечном) и g ' (x) не обращается в нуль в (a, b). Пусть известно, что
Тогда говорят, что отношение
то и
Доказательство. Пусть А конечно. Для заданного как угодно малого числа ε > 0 выберем х 0 так, чтобы в интервале (а, x 0) выполнялось неравенство
Определим функцию D (x, x 0) из условия
Имеем
при x → a + 0. Применяя к отрезку [ x, x 0] теорему Коши, получаем, что некоторой точки с
Отсюда для всех х, для которых | D (x, x 0) - 1 | < ε, находим
Так как ε произвольно мало, то
Формула Тейлора.
Пусть функция f (x) имеет в точке а и некоторой её окрестности производные порядка n + 1. Пусть x ≠ a есть любое значение аргумента из указанной окрестности, тогда между точками а и х найдётся такая точка с, что справедлива формула
Доказательство. Положим
Функция F (x) имеет производные до порядка n + 1 вместе с функцией f (x). Функция G (x) имеет производные всех порядков, причём её производные положительны при х > a. Легко проверить, что
и поэтому F (m)(а) = f (m)(а) – f (m)(а) = 0 при m = 0, 1, …, n. Так как G (m)(а) = 0 при m = 0, 1, …, n, то выполнены все условия обобщённой формулы Коши. При этом очевидно, что F (n + 1)(х) = f (n + 1)(х), G (n + 1)(х) = (n + 1)! Применение обобщённой формулы Коши к этим функциям приводит к соотношению
откуда и получается формула Тейлора с остаточным членом в форме Лагранжа
Как видно, функция раскладывается на две части. Главная часть
называется многочленом Тейлора порядка n. Второе слагаемое
называется остаточным членом функции в форме Лагранжа.
где с
|
|||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 434; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.26.246 (0.008 с.) |
 является угловым коэффициентом секущей, проходящей через точки M1 (a; f (a)) и M2(b; f (b)) графика функции у = f (x), a f ' (c) — угловой коэффициент касательной к графику в точке (c; f (c)). Из теоремы Лагранжа следует, что существует точка " c " такая, что касательная к графику в точке (c; f (c)) параллельна секущей M1M2. Таких точек может быть и несколько, но, по крайней мере, одна всегда существует.
является угловым коэффициентом секущей, проходящей через точки M1 (a; f (a)) и M2(b; f (b)) графика функции у = f (x), a f ' (c) — угловой коэффициент касательной к графику в точке (c; f (c)). Из теоремы Лагранжа следует, что существует точка " c " такая, что касательная к графику в точке (c; f (c)) параллельна секущей M1M2. Таких точек может быть и несколько, но, по крайней мере, одна всегда существует.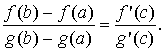
 .
. ,
, .
.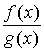
 .
.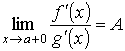 ,
, .
. .
. [ а, x 0], то существует такая точка с
[ а, x 0], то существует такая точка с 
 .
.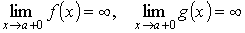 .
. .
.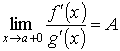 ,
, .
.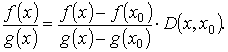 .
.
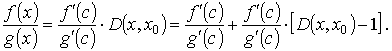

 .
. ,
, 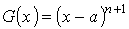 .
.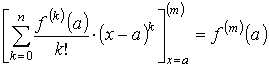 ,
,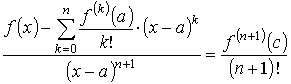 ,
, .
.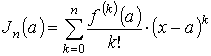
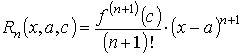
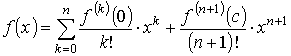 ,
,


