
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Алгебраичность конечного расширения.
Расширение полей наз. алгебраическим, если каждый эл-т е явл. алгебраическим над F. Теорема. Каждое конечное расширение ЕᴐF ([E:F]< Д-во: Пусть ЕᴐF – конечное расширение степени n: [E:F]=n. Возьмем произвольный эл-т a?E\{0}. С-ма векторов 1,а,а2,…,an л.з. над F [
25. Простое расширение Пусть ЕᴐF– расширение полей, а?Е, Теорема. 1. F(a) – поле. 2. F(a) - наименьшее подполе Е, которое содержит F, a. 3. F(a) – пересечение всех подполей поля Е, которое содержит F,a. Д-во: (1)
F(a)сЕ подполе Е, зн. F(a) – поле. Поле F(a) наз. простым расширением поля F. Эл-т а наз. примитивным эл-том этого расширения. Пусть ЕᴐF, a?E. 1. Если а – алгебр.эл-т над полем F, то F(a) наз. простым алгебр.расширением. 2. Если а – трансцендентный эл-т, то F(a) наз. простым трансцендентным расширением. Примеры. 1. Q(
2.
26. Простое расширение Пусть ЕᴐF– расширение полей, а?Е, Теорема. 1. F(a) – поле. 2. F(a) - наименьшее подполе Е, которое содержит F, a. 3. F(a) – пересечение всех подполей поля Е, которое содержит F,a. Д-во: (2) FcF(a). Д-ть, что f(x)=c, g(x)=1. F(a) – наименьшее поле, которое содержит F,a. Если TcE, которое содержит F,a, то F(a)cT.
f(a)=anan+…+a1a+a0?T ?F?T?F?T?F g(a)=bmam+…+b1a+b0?T ?F?T?F?T?F Получили, что каждый эл-т поля F(a) (3) Пусть Р – пересечение всех подполей поля Е, которое содержит F и а. Докажем, что P=F(a). Т.к.каждое из полей содержит F и a, то пересечение этих подполей тоже содержит F и а. Пересечение Р содержится в каждом из таких полей, т.е. PcF(a). Т.к. F(a) – наименьшее из подполей Е, то F(a)cP. Поле F(a) наз. простым расширением поля F. Эл-т а наз. примитивным эл-том этого расширения.
Пусть ЕᴐF, a?E. 1. Если а – алгебр.эл-т над полем F, то F(a) наз. простым алгебр.расширением. 2. Если а – трансцендентный эл-т, то F(a) наз. простым трансцендентным расширением. Примеры. 1. Q(
2.
Квадратичное расширение поля. Критерий квадратичности расширения поля. Пусть F- числовое поле, d?F, Теорема. Е – квадратичное расширение поля F ó когда степень расширения =2, т.е. [E:F]=2. Д-во: => F- числовое поле [подполе C], d?F,
=> [E:F]=2. <= [E:F]=2, ᴲa?E\F и степень этого эл-та над полем F =2. Если рассм. 1,а,а2, то они л.з., зн. ᴲс0,с1?F | a2+c1a+c0=0. Зн., а – корень полинома f(x)= x2+c1x+c0 => E=F(a)=F( [E:F(a)][F(a):F]=[E:F]=2 => E=F(a)=F( =1 =2 28. Теорема об избавлении от иррациональности в знаменателе дроби: построение взаимно простых полиномов Теорема: Пусть Д-во:
Ранее было доказано, что если p(x) не приводим над полем От противного если бы
u(x) Возьмем x=a: u(a) u(a)
t=h(a)
29. Теорема об избавлении от иррациональности в знаменателе дроби: единственность. Построение поля Теорема: Пусть Д-во: единственность Пусть t=h(a) t= deg h(x) deg тогда а - корень полинома h(a)-
возможны два случая: если [ Противоречие: т.к. а – алгебраический элемент степени n над F и степень полинома наименьшей степени над F корнем которого является а= n] Следствие 1: Пусть E [то есть степень ровна степени min полинома элемента а надF,другими словами векторы 1,а,…, Д-во: Т. обр. каждый элемент из F(a) имеет вид:
=> - Допустим Это значит, что a- корень полинома f(x)= f(a)=0,но f(x) Конец док-ва.
|
||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 491; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.178.240 (0.017 с.) |
 ) явл. алгебраическим над F.
) явл. алгебраическим над F. (n+1) векторов в n-мерном пространстве л.з.], это зн., что ᴲ такие с0,с1,…,сn?F не все =0, такие что с0+с1а+…сnаn=0 => эл-т а явл. корнем полинома f(x)=anxn+…+a1x+a0, f(x)≠0 => a – алгебр. эл-т над F.
(n+1) векторов в n-мерном пространстве л.з.], это зн., что ᴲ такие с0,с1,…,сn?F не все =0, такие что с0+с1а+…сnаn=0 => эл-т а явл. корнем полинома f(x)=anxn+…+a1x+a0, f(x)≠0 => a – алгебр. эл-т над F. поля
поля  с помощью примитивного элемента. Поле
с помощью примитивного элемента. Поле  .
. ] подкольцо, a-1?F(a), 1?F(a).
] подкольцо, a-1?F(a), 1?F(a).

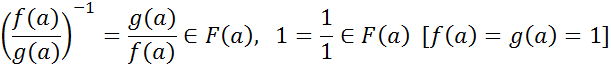
 ) – простое алгебр. расширение.
) – простое алгебр. расширение. r1+r2
r1+r2  - простое трансцендентное расширение поля Q, которое получается присоединением к полю Q трансцендентного эл-та
- простое трансцендентное расширение поля Q, которое получается присоединением к полю Q трансцендентного эл-та  .
.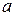 . Простое алгебраическое расширение и простое трансцендентное расширение: определение, примеры.
. Простое алгебраическое расширение и простое трансцендентное расширение: определение, примеры. .
. c?F.
c?F.  .
. . a?F(a),
. a?F(a),  .
.  ,
, 
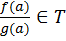 => F(a)cT.
=> F(a)cT. ) – простое алгебр. расширение.
) – простое алгебр. расширение. r1+r2
r1+r2  - простое трансцендентное расширение поля Q, которое получается присоединением к полю Q трансцендентного эл-та
- простое трансцендентное расширение поля Q, которое получается присоединением к полю Q трансцендентного эл-та  .
.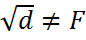 . Поле F(
. Поле F( ) наз. квадратичным расширением поля F.
) наз. квадратичным расширением поля F. F.
F.

 .
.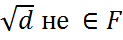 .
. и
и  .
. -расширение полей,
-расширение полей,  -алгебраический элемент степени n под F, тогда каждый элемент
-алгебраический элемент степени n под F, тогда каждый элемент  (а) из простого расширения F(a),можно представить в виде t=h(a),где h(x) – полином над полем F
(а) из простого расширения F(a),можно представить в виде t=h(a),где h(x) – полином над полем F  степень которого deg h(x)
степень которого deg h(x)  такое представление единственное.
такое представление единственное. F(a)=
F(a)= 


 p(x)
p(x)  deg p(x)=n элемента a, min полином p(x) не приводим.
deg p(x)=n элемента a, min полином p(x) не приводим. , то
, то  возможны только два случая:
возможны только два случая: 

 u(x),v(x)
u(x),v(x) 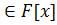
 v(x)p(x)=1
v(x)p(x)=1 v(a)
v(a) 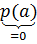 =1
=1
 =
= 
 разделим с остатком на
разделим с остатком на 


 , deg h(x)
, deg h(x)  n-1
n-1 для алгебраического элемента
для алгебраического элемента  такое представление единственное.
такое представление единственное. , где t=h(a), t=
, где t=h(a), t= 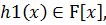
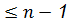



 , то это полином степени
, то это полином степени  над F корнем которого является а.?!
над F корнем которого является а.?! F -расширение полей, а
F -расширение полей, а  Е-алгеброический элемент степени n над F, тогда F(a)=
Е-алгеброический элемент степени n над F, тогда F(a)=  и степень[F(a):F]=n
и степень[F(a):F]=n базис F(a)над F]
базис F(a)над F] F(a) можно записать в виде t=h(a), где h(x)
F(a) можно записать в виде t=h(a), где h(x)  F[x], deg h(x)
F[x], deg h(x)  n-1
n-1



 , f(x)
, f(x)  deg p(x)=n?!
deg p(x)=n?!


