
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расширение поля. Степень расширения. Расширение как линейное пространство. Мультипликативность степени расширения(система образующих).
Опр. Если Р-подполе поля F, то F –наз. расширением поля Р. Замечание: В этом случае F можно рассматривать как линейное пространство над полем Р. Опр. Размерность F над Р наз. степенью расширения F над Р. Обозначение - [F:P] Если F над Р <∞, то F наз. конечным расширением поля Р. Другими словами F конечное над Р. Теорема. Пусть L, K, F – поля. L Верно равенство: [L:K][K:F]=[L:F]- мультипликативность степени расширения. Док-во: · пусть степень расширения [L:K]=S, зн. Имеем базисс из S-элементов(векторов) u1, u2, ….., us · пусть степень расширения [K:F]=t,тогда расширение K⊃F имеет базисс из t-векторов: v1, v2, ….,vt Докажем, чтос тепеньвекторов ui vj, где 1 2) Докажем, что: система векторов (*) над F
· Пусть х с1,с2, ….., сs · v1, v2, ….,vt –базис К над F, поэтому каждый вектор сi линейной комбинацией векторов v1, v2, ….,vt с коэффициентами из поля F. Т.е. мы получим · Подставим Образом(*)-система образующих линейного пространства Lнад полем F 3) Так как в базисе (*) st векторов, то степень расширения [L:F]=st=[L:K][K:F] ◄ 19.Характеристика поля: определения, примеры, свойства. Опр. Пусть P-поле, для Если для некоторого n Обозн. char P=0 или char P=p>0. Примеры. 1. Поле Q, R, C имеет характеристику 0. char Q=0, char R=0,char C=0 2. Кольцо классов вычетов
Замечание. 1) Примерами полей положительной хар-ки явл. все конечные поля, т.е. поля которые состоят из конечного числа эл-ов. Но существуют и бесконечные поля,которые имеют положительную характеристику. 2) Теорема. Если поле Р имеет хар-ку р>0,то р-простое число. Док-во. (от противного)
Из рав-ва р=s*t,где s<p, t<p⇒ (s*1)(t*1)=st*1=p*1=0,но в поле нет делителей 0,поэтому s*1=0 или t*1=0.Противоречие. Свойства 1. а) если хар-ка поля Р=р, то б) если р=0, то а) char P=p, пусть n=p* б) char P=0, то из n*a=(n*1)* char P=0⇒n=0-противоречие. 2. Если char P=p, то Док-во. ММИ по n. n=1:
Значит, Пусть утверждение верно при n=k-1. n=k: Следствие. Если характеристика Р=р, то
20. Пересечение подполей как подполе поля. Простое поле: определение, примеры, Изоморфизм простого подполя Св-во 1. Если Р поле, Р1,Р2 – подполя поля Р, тогда Р1∩ Р2 – подполе поля Р. ►1) 0 и 1 поля Р содержаться и в Р1 и в Р2 (по определению подполя)⇒0 и 1 2.) а) Рассмотрим 2 этапа a и b b) Следствие. Пересечение Рi (i Опр. Поле в котором нет не одного собственного подполя, наз простым. Св-во 2. Q, Zp- простые поля. Теорема. В произвольно поле Р содержится ровно 1 или ровно одно подполе Р: 1) если char P=0, то Р0 изоморфно Q. 2)если char P=р, то Р0 Алгебраические и трансцендентные эл-ты: определение, пр-ры. Минимальный полином. Степень алгебраического эл-та. Неприводимость миним. полинома. Пусть ЕᴐF расширение полей. Эл-т а?Е наз. алгебраическим над F, если ᴲ ненулевой полином f(x)?F[x] такой, что f(a)=0. Если такого полинома не ᴲ, это зн., что Замечание. Если F=Q – слова «над полем Q» не говорят. Пример. Рассм. эл-т а= a-3= Пусть расширение полей ЕᴐF, а?Е. Минимальным полиномом эл-та а наз. ненулевой полином f(x)?F[x] наименьшей степени со старшим коэф-том 1, такой что f(a)=0. Степень полинома f(х) наз. степенью эл-та а. Пример. Явл. ли число алгебраическим? Если да, то найти его степень. 1. 2. a=
Утверждение. Миним. полином f(x) эл-та а неприводим. Д-во: Пусть f(x)=g(x)h(x), f(x),g(x),h(x)?F[x], deg g(x)<deg f(x), deg h(x)<deg f(x). 0=f(a)=g(a)h(a)
|
||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 1272; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.171.121 (0.013 с.) |
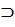 K⊃F. [L:K]<∞,[K:F]<∞,тогда L⊃F-конечное расширение, т.е. [L:F]<∞.
K⊃F. [L:K]<∞,[K:F]<∞,тогда L⊃F-конечное расширение, т.е. [L:F]<∞. L.
L.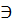 K
K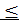 i
i  S, 1
S, 1  (*)
(*)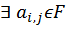 , 1
, 1  i
i  S, 1
S, 1 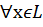 можно представить в виде линейной комбинации векторов из системы (*).
можно представить в виде линейной комбинации векторов из системы (*). К такой что х= с1u1+ …+ с1u1=
К такой что х= с1u1+ …+ с1u1=  (1)
(1) (2)
(2)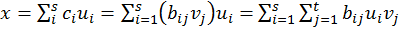 . Таким
. Таким n
n  N элемент n*1=
N элемент n*1=  неравный 0,то говорят, что поле Р имеет характеристику 0.
неравный 0,то говорят, что поле Р имеет характеристику 0. -поле ⇔m=p-простое число
-поле ⇔m=p-простое число -поле классов вычетов целых чисел, но поле Р состоит из р эл-ов. char
-поле классов вычетов целых чисел, но поле Р состоит из р эл-ов. char  /n
/n  p имеет место n*a=0.
p имеет место n*a=0. и
и  n*a
n*a  0
0 , тогда n*a=
, тогда n*a= 
 =0⇒n*1=0.
=0⇒n*1=0. то верно рав-но
то верно рав-но  .
.



 .
.

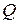 или
или  .
. Р1∩ Р2.
Р1∩ Р2. a, b
a, b  подполей поля Р,является подполем поля Р.
подполей поля Р,является подполем поля Р. Zp
Zp f(x)?F[x] f(a)≠0, то эл-т а наз. трансцендентным над F.
f(x)?F[x] f(a)≠0, то эл-т а наз. трансцендентным над F. .
. , (a-3)3=7-2i, (a-3)3-7=-2i, ((a-3)3-7)2=(-2i)2, ((a-3)3-7)2=-4, ((a-3)3-7)2+4=0, f(x)= ((a-3)3-7)2+4 => а – алгебраическое число.
, (a-3)3=7-2i, (a-3)3-7=-2i, ((a-3)3-7)2=(-2i)2, ((a-3)3-7)2=-4, ((a-3)3-7)2+4=0, f(x)= ((a-3)3-7)2+4 => а – алгебраическое число. =a, 5-а2=0, а2-5=0, f(x)=x2-5 алг.эл-т, f(x) – миним.полином, f(x) – неприводим по критерию Эйзенштейна, р=5.
=a, 5-а2=0, а2-5=0, f(x)=x2-5 алг.эл-т, f(x) – миним.полином, f(x) – неприводим по критерию Эйзенштейна, р=5.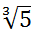 , a3-5=0, f(x)=x3-5 – по критерию Эйзенштейна неприводим.
, a3-5=0, f(x)=x3-5 – по критерию Эйзенштейна неприводим.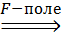 [нет делителей 0] g(a)=0 или h(a)=0 (противоречие).
[нет делителей 0] g(a)=0 или h(a)=0 (противоречие).


