
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теплопередача через плоскую однослойную стенку при граничных условиях III-рода
Теплопередача – процесс теплообмена между двумя средами (теплоносителями), разделёнными стенкой (перегородкой). В этом случае при граничных условиях III-рода задаются температуры сред теплоносителей, коэффициенты теплоотдачи
Требуется найти плотность теплового потока, тепловой поток и температуру поверхности стенки. Согласно закону Ньютона-Рихмана плотность теплового потока между горячей средой и поверхностью стенки:
По закону Фурье этот же поток передаётся теплопроводностью:
Этот же тепловой поток согласно закону Ньютона-Рихмана от наружной поверхности стенки отдаётся холодной среде:
Выражая из этих уравнений разности температур и складывая между собой, мы окончательно получаем выражение для плотности теплового потока q:
Обозначим величину
К – коэффициент теплопередачи через плоскую однослойную однородную стенку. Он представляет собой количество теплоты, передаваемое в единицу времени через единицу поверхности при разности температур между средами в один градус. Значения коэффициентов теплопередачи для различных видов теплообмена будут даны в таблице в разделе конвективного теплообмена. Коэффициент теплопередачи всегда меньше меньшего α. Для того чтобы увеличить теплопередачу, нужно увеличить меньшее α.
Тепловой поток
Величина обратная коэффициенту теплопередачи – полное термическое сопротивление теплопередачи:
где
Полное количество теплоты, передаваемое через стенку за время τ
Коэффициента теплопередачи не является термофизическим коэффициентом, его нет в справочниках. Он рассчитывается по формуле (3.11). Из (3.9) легко найти температуры горячей и холодной стенок:
Теплопередача через многослойную плоскую стенку при граничных условиях III-рода Пусть заданы температуры сред
Аналогично формуле (3.9) записывают уравнение сохранения плотности теплового потока q, выражая разность температур и складывая почленно полученные выражения плотности теплового потока
Коэффициент теплопередачи:
Из уравнения (3.16), определяя плотность теплового потока, находим температуры на поверхностях стенки Получение эмпирических формул или Критериальных зависимостей Моделированием называется метод экспериментального изучения модели используемой вместо натурного явления. Модель выбирается так, чтобы результаты эксперимента можно было распространить на натуральное явление. Моделирование представляется двумя этапами: – создание модели; – измерение и наблюдение на модели. По результатам измерения и наблюдения на модели определяется, например, экспериментальная зависимость коэффициента теплоотдачи вида:
Эта зависимость пригодна для натурного объекта при следующем условии: если процессы теплообмена в модели и в натурном образце подобны. Процессы будут подобны, если модель геометрически подобна натурному образцу (в n раз меньше или больше), и числа подобия модели и объекта равны между собой. По данным измерений подсчитываются значения:
и соответствующее им (a рассчитано по формуле (2)) Зависимость между числами подобиями представлена степенной функцией:
где с, n, m – постоянные безразмерные числа. Предположим, что число Нуссельта Nu зависит только от числа Рейнольдса Re (опыты проводятся с теплоносителями, у которых число Прандтля постоянно
Логарифмируя выражение (3) получаем:
Обозначим члены следующим образом:
Показатель степени n определяется как тангенс угла наклона, образованного прямой в логарифмических координатах с осью абсцисс (Х). Постоянная С в уравнении (3) определяется как:
Проверкой правильности степенной зависимости является тот факт, что в логарифмических координатах либо в логарифмической анаморфозе все точки укладываются на одну прямую.
Если искомое число Nu является функцией двух переменных – Re и Pr, на графике в логарифмических координатах получается семейство прямых. Второй аргумент (Pr) берётся в качестве параметра.
Тогда по одной из прямых определяется показатель n как tgj, затем опытные данные представляются на графике в виде:
Тогда m определяется как Затем определяем постоянную C из уравнения (2):
Сущёствуют специальные программы для расчёта c, n, m.
|
||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 903; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.160.156 (0.01 с.) |
 между горячей средой и стенкой и
между горячей средой и стенкой и  между стенкой и холодной средой, т.е. задаётся закон теплообмена. Также задаётся коэффициент теплопроводности
между стенкой и холодной средой, т.е. задаётся закон теплообмена. Также задаётся коэффициент теплопроводности  и толщина стенки δ.
и толщина стенки δ.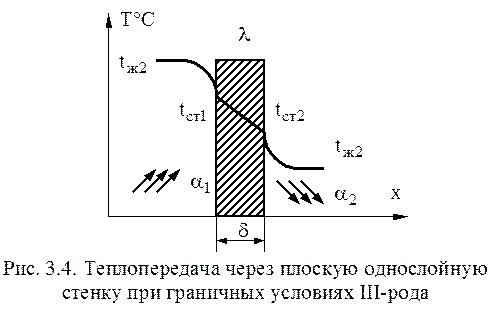
 . (3.9)
. (3.9)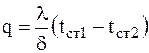 . (3.9)
. (3.9)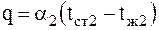 . (3.9)
. (3.9) ,
, 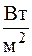 . (3.10)
. (3.10)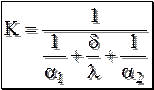 ,
,  (3.11)
(3.11) . (3.12)
. (3.12) . (3.13)
. (3.13)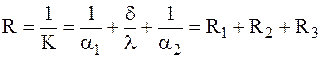 , (3.14)
, (3.14)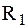 – термическое сопротивление теплоотдачи со стороны горячей жидкости;
– термическое сопротивление теплоотдачи со стороны горячей жидкости; – термическое сопротивление стенки (чем меньше l, тем выше
– термическое сопротивление стенки (чем меньше l, тем выше 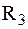 – термическое сопротивление теплоотдачи от стенки к холодной среде.
– термическое сопротивление теплоотдачи от стенки к холодной среде.  .
. , Дж.
, Дж. , (3.15)
, (3.15)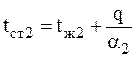 .
. и
и  , коэффициенты теплоотдачи
, коэффициенты теплоотдачи 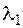 ,
,  и
и  , толщина слоёв стенки
, толщина слоёв стенки  ,
,  и
и  .
.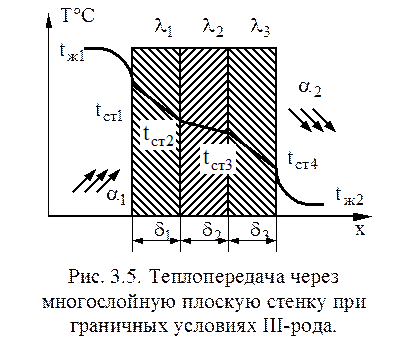
 ,
,  ,
, 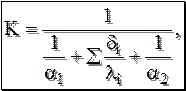
 (3.18)
(3.18)
 (3.19)
(3.19) ,
,  и температуры на границах слоёв
и температуры на границах слоёв  ,
,  .
.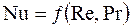 . (13.28)
. (13.28)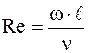 ,
, 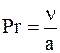 ,
,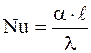 .
.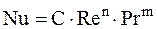 , (13.29)
, (13.29) ). В этом случае:
). В этом случае: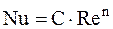 . (13.30)
. (13.30)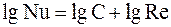 . (13.31)
. (13.31)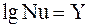 ,
, 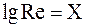 ,
, 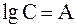 . Получаем уравнение прямой линии в логарифмических координатах (рис. 13.4):
. Получаем уравнение прямой линии в логарифмических координатах (рис. 13.4):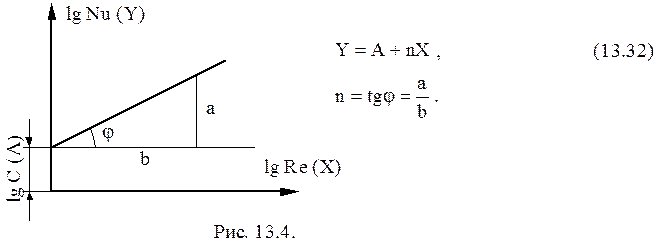
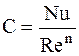 . (13.33)
. (13.33)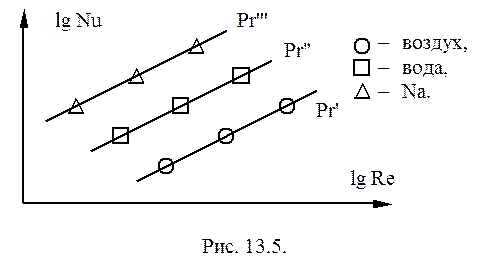
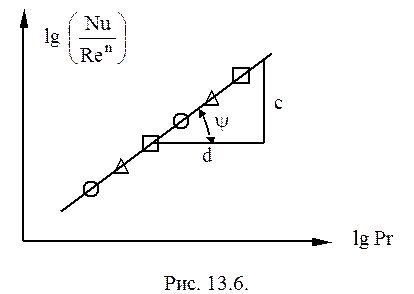
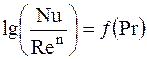 .
.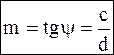 . (13.34)
. (13.34)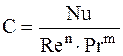 . (13.35)
. (13.35)


