
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод непрямих найменших квадратів
Непрямий метод найменших квадратів (НМНК) використовують для знаходження оцінок точно ототожнених моделей. Процедуру знаходження структурних параметрів симультативної моделі НМНК можна умовно поділити на 3 етапи: 1. Для заданої структурної моделі будуємо скорочену форму у згорнутому та розгорнутому вираженні. 2. Оскільки екзогенні змінні у скороченій формі є не стохастичними, тобто не залежать від випадкової величини, то для знаходження оцінок коефіцієнтів скороченої форми застосовують метод найменших квадратів. 3. На основі системи параметричних взаємозв’язків та оцінених коефіцієнтів скороченої форми знаходимо оцінки структурних параметрів моделі. Оскільки рівняння точно ототожнене, то між структурними параметрами та параметрами скороченої форми є взаємооднозначна відповідність – ці оцінки будуть однозначними. Оцінки параметрів симультативної моделі, знайдені НМНК, є оцінками з відхиленнями, які зникають із збільшенням вибірки, ці оцінки є консистентними. Недоліком НМНК є те, що його застосовують тільки для точно ототожнених моделей. Двокроковий метод найменших квадратів Застосування для знаходження оцінок невизначених параметрів та пере ототожнених моделей. Ідея полягає у записані стохастичних ендогенних змінних деякими допоміжними інструментальними змінними, які є незалежними від випадкових величин з р-ння. Розглянемо деяке і -те рівняння симультативної-моделі При цьому Якщо у р-ння (*) є ще стохастичні ендогенні змінні то аналогічні допоміжні змінні необхідно побудувати для них. Рівняння (*) після усунення стохастичних ендогенних змінних буде мати вигляд Враховуючи що у рівнянні (**) не включені стохастичні змінні то для знаходження оцінок параметрів цього р-ння можна використовувати МНК. Включає такі етапи 1. будуємо допоміжні змінні для кожної ендогенної змінної моделі. Для цього застосовують звичайний МНК, а допоміжну змінну будують у вигляді
2. замість ендогенних змінних, які наявні в правій частині р-ння що оцінюють, записують допоміжні змінні 3. оскільки після введення допоміжних змінних у правій частині р-ння не має стохастичних змінних то для оцінки параметрів такого р-ння застосовують МНК. Двокроковий МНК можна застосовувати для оцінки окремого р-ння моделі.
Послідовне оцінювання параметрів дистрибутивно-лагових моделей Нехай необхідно оцінити параметри ДЛМ. Метод включає такі етапи: 1) оцінюють модель Побудову моделей припиняють, якщо настає хоча б одна з таких умов: 1) оцінка будь-якого з параметрів 2) статистична незначущість параметра Для перетворення статистичних значень парам. Знаходимо критичне значення t-стат. за таблицями розподілу Стюдента при заданому рінвні значущості Емпіричне знач. t-стат. знаходимо за формулою Недоліки методу послідовного оцінювання: 1) наперед невідомою є довжина лагу; 2) можливість наявності мультиколінеарності між лаговими змінними; 3) зменшення ступенів свободи на кожному наступному етапі.
Модель Койка Роблять 2 припущення: 1) Коефіцієнти Параметр Враховуючи припущення (1) нескінченно ДЛМ можна записати у вигляді: Модель (2) з запізненням в 1 період Модель (3) домножимо на Від моделі (2) віднімемо модель (4)
Має такі особливості: 1) у ДЛМ ми отримуємо авто-регресійну модель; 2) під час оцінювання моделі (5) необхідно перевірити чи змінна
Переваги: 1) чітке припущення що всі 27. Модель адаптивних очікувань (перша модель модифікації Койка) Підхід Койка до дистрибутивно-лагових моделей Койк запропонував досить цікавий метод оцінки дистрибутивно-лагових моделей. Припустимо, ми починаємо з дистрибутивно-лагової моделі з невизначеним лaгом ( - припускаючи, що λ можуть бути від'ємними, Койк абстрагувався від зміни знака коефіцієнта при βі; - завдяки тому, що λ<1 віддалені за часом, значення βі стали менш впливовими, ніж поточні; - сума βі, яка складає довгостроковий мультиплікатор, є скінченною, тобто . як результат (1.4), модель з кінцевим лагом (1.5) можна записати таким чином: .
28. Модель часткових пристусувань(друга МОДИФІКАЦІЇ моделі Койка) Як бачимо, модель (1.6) також незручна для оцінки, оскільки залишається дуже велика (фактично нескінченна) кількість оцінюваних параметрів, крім того, параметр λ входить до моделі в нелінійній формі: тобто метод лінійної (за параметрами) регресії не можна застосувати до цієї моделі. Але Койк пропонує модифікований метод, який полягає в тому, що в модель (1.6) вводиться затримка на один період. Виходячи з цього, модель записується таким чином:
Далі помножуємо (1.7) на λ і отримаємо:
Віднявши (1.8) від (1.6), маємо:
де Зазначимо деякі особливості трансформації Койка. 1. Трансформація Койка переводить дистрибутивно-лагову модель в авторегресивну, оскільки серед незалежних змінних залишається уt-1. 2. Поява уt-1 може спричинити ряд статистичних проблем: уt-1, як і уt, - стохастична; це означає, що в модель ми вводимо стохастичну змінну. 3. У початковій моделі (1.3) помилка дорівнювала εt, а в перетвореній 4. Наявність лагового значення у порушує одне з припущень d-тесту Дарбіна-Уотсона. Отже, нам потрібно розробити альтернативу для тестування серійної кореляції при лаговому у. Цією альтернативою є h-тест Дарбіна.
|
|||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 301; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.216.174 (0.014 с.) |
 Якщо ендогенна змінна
Якщо ендогенна змінна  є стохастичною то для неї необхідно побудувати допоміжну змінну, яка буде мати вигляд
є стохастичною то для неї необхідно побудувати допоміжну змінну, яка буде мати вигляд  - де
- де  -допоміжна змінна;
-допоміжна змінна; 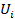 -випадкова величина для якої використовують усі припущення класичного кореляційно-регресійного аналізу.
-випадкова величина для якої використовують усі припущення класичного кореляційно-регресійного аналізу.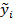 буде тісно корелювати зі змінною
буде тісно корелювати зі змінною 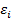 .
. ;
; 
 (знаходимо значення допоміжних змінних для кожного спостереження)
(знаходимо значення допоміжних змінних для кожного спостереження)
 2) оцінюють модель
2) оцінюють модель 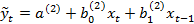 ; 3) оцінюють модель
; 3) оцінюють модель 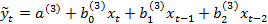
 змінює знак
змінює знак формують таку нульову гіпотезу: параметр
формують таку нульову гіпотезу: параметр 
 к-ті ступенів вільності 0=n-k-1 (к-ть змін в правій частині) за таб. нормального розподілу при заданому рівні
к-ті ступенів вільності 0=n-k-1 (к-ть змін в правій частині) за таб. нормального розподілу при заданому рівні  .
.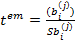 . Якщо
. Якщо  то нульову гіпотезу відхиляють і з довірчою ймовірн. р=1- а можна стверджувати що парам. статистично значущий. В протилежному випадку нульову гіпотезу приймають.
то нульову гіпотезу відхиляють і з довірчою ймовірн. р=1- а можна стверджувати що парам. статистично значущий. В протилежному випадку нульову гіпотезу приймають. мають одинаковий знак; 2) Коефіцієнти
мають одинаковий знак; 2) Коефіцієнти 
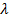 наз. темп зростання ДЛ, а
наз. темп зростання ДЛ, а  швидкість прискорювання
швидкість прискорювання


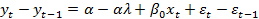
 для оцінювання параметрів моделі (5) можна застосувати МНК
для оцінювання параметрів моделі (5) можна застосувати МНК є не стохастична, тобто чи не зал. від випадкової величини
є не стохастична, тобто чи не зал. від випадкової величини 
 і змін в геометричній прогресії; 2) мат. модель.
і змін в геометричній прогресії; 2) мат. модель. =
=  ). Припускаючи, що βі мають той самий знак, Койк припустив також, що вони змінюються в геометричній прогресії:
). Припускаючи, що βі мають той самий знак, Койк припустив також, що вони змінюються в геометричній прогресії: 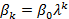 k = 0, 1, …, (1.4) де λ такі, що 0 < λ < 1 – темп зменшення дистрибутивного лагу, а (1- λ) – швидкість пристосування. Співвідношення (1.4) показує, що кожний наступний коефіцієнт β менший, ніж попередній (оскільки λ< 1), тобто з кожним наступним кроком у минуле вплив лaгу на уt поступово зменшується, що є досить імовірним припущенням. Значення лaгового коефіцієнта βк -залежить, крім загального β0 також і від λ. Чим ближче значення λ до 1, тим повільніший темп зменшення βк, а чим ближче він до 0, тим швидше спадає βк. У попередньому випадку віддалені в минулому значення х досить сильно впливали на уt, тоді як у нашому випадку їхній вплив на уt швидко зменшується. Слід зазначити, що метод Койка має такі переваги:
k = 0, 1, …, (1.4) де λ такі, що 0 < λ < 1 – темп зменшення дистрибутивного лагу, а (1- λ) – швидкість пристосування. Співвідношення (1.4) показує, що кожний наступний коефіцієнт β менший, ніж попередній (оскільки λ< 1), тобто з кожним наступним кроком у минуле вплив лaгу на уt поступово зменшується, що є досить імовірним припущенням. Значення лaгового коефіцієнта βк -залежить, крім загального β0 також і від λ. Чим ближче значення λ до 1, тим повільніший темп зменшення βк, а чим ближче він до 0, тим швидше спадає βк. У попередньому випадку віддалені в минулому значення х досить сильно впливали на уt, тоді як у нашому випадку їхній вплив на уt швидко зменшується. Слід зазначити, що метод Койка має такі переваги: (1.5)
(1.5) (1.6)
(1.6)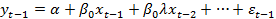 (1.7)
(1.7) (1.8)
(1.8) (1.10)
(1.10) . Ця процедура відома як перетворення Койка. Порівнюючи (1.10) з (1.3), бачимо надзвичайне спрощення моделі. Якщо раніше нам треба було оцінювати параметр αλ та нескінченну кількість параметрів βі, тепер достатньо оцінити лише три змінних: α,βо і λ, тобто немає причин очікувати мультиколінеарність. Фактично ми позбулись мультиколінеарності заміною хt-1, хt-2 … на одну змінну, тобто уt-1.
. Ця процедура відома як перетворення Койка. Порівнюючи (1.10) з (1.3), бачимо надзвичайне спрощення моделі. Якщо раніше нам треба було оцінювати параметр αλ та нескінченну кількість параметрів βі, тепер достатньо оцінити лише три змінних: α,βо і λ, тобто немає причин очікувати мультиколінеарність. Фактично ми позбулись мультиколінеарності заміною хt-1, хt-2 … на одну змінну, тобто уt-1.


