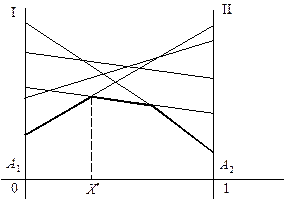Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Нехай маємо скінченну матричну гру з платіжною матрицею
Оптимальні змішані стратегії гравців А і В за теоремою визначають вектори
Використання оптимальної змішаної стратегії гравцем А має забезпечувати виграш на рівні, не меншому, ніж ціна гри за умови вибору гравцем В будь-яких стратегій. Математично ця умова записується так [4; с. 218]:
З другого боку, використання оптимальної змішаної стратегії гравцем В має забезпечувати за будь-яких стратегій гравця А програш, що не перевищує ціну гри u, тобто [4; с. 218]:
Ці співвідношення використовуються для знаходження розв’язку гри. 1.5. Геометрична інтерпретація гри 2´2
Найпростішим випадком скінченної гри є парна гра, коли у кожного учасника є дві стратегії [13; с. 42].
Розглянемо випадок, коли гра не має сідлової точки. Отже, Згідно з основною теоремою теорії ігор, якщо гравець А дотримується своєї оптимальної стратегії, то виграш буде дорівнювати ціні гри. Отже, якщо гравець А притримуватиметься своєї оптимальної стратегії
Оскільки
Розв’язавши дане рівняння відносно невідомого
тоді: Провівши аналогічні міркування стосовно гравця В, маємо:
Оскільки
Розв’язавши це рівняння відносно невідомого
тоді: Ціну гри u знаходять, підставляючи значення
Розв’язку гри 2 ´ 2 можна дати наочну геометричну інтерпретацію. Розглянемо гру з платіжною матрицею виду [16; с. 434]:
Відмітимо на осі абсцис відрізок довжиною, що дорівнює одиниці (рис. 1.3). Лівий кінець відрізка (точка з абсцисою х = 0) буде відповідати стратегії А 1, а правий кінець (х = 1) – стратегії А 2, всі проміжні точки цього відрізка відповідатимуть змішаним стратегіям гравця А, причому імовірність х 1 стратегії А 1 буде дорівнювати відстані від точки Р до правого кінця відрізка, а ймовірність х 2 стратегії А 2 – відстані до лівого кінця відрізка. Проведемо через точки А 1 та А 2 два перпендикуляри до осі абсцис: вісь І і вісь ІІ. На першій з них відмітимо виграш за вибору стратегії А 1, а на другій – за стратегії А 2.
Нехай противник вибрав стратегію В 1, їй відповідають на осях І та ІІ дві точки В 1, причому довжина відрізка А 1 В 1 дорівнює а 11, а довжина відрізка А 2 В 1 дорівнює а 12. Аналогічно будуємо пряму В 2 В 2, яка відповідає стратегії В 2. Необхідно знайти оптимальну стратегію Х *, таку, за якої мінімальний виграш гравця А буде максимальним. Для цього виділимо жирною лінією на малюнку нижню межу виграшу за умови вибору стратегій В 1 та В 2, тобто ламану лінію В 1 МВ 2. На цій межі знаходяться значення мінімального виграшу гравця А за будь-якої його змішаної стратегії. Очевидно, що найкраще з можливих мінімальних значень у нашому прикладі знаходиться в точці М, а в загальному випадку відповідає тій точці, де крива, що позначає мінімальний виграш гравця А, набуває максимального значення. Ордината цієї точки є ціною гри u. Відстань до лівого кінця відрізка х 2 та відстань до правого кінця відрізка — х 1 дорівнюють відповідно ймовірностям стратегій А 2 та А 1.
Рис. 1.3. Графічна інтерпретація гри 2´2 Джерело: [16; с. 435].
Геометрична інтерпретація дає також змогу наочно зобразити нижню та верхню ціну гри (рис. 1.4). Для нашого прикладу нижньою ціною гри є величина відрізка А 2 В 2, а верхньою ціною гри – А 2 В 1.
Рис. 1.4. Геометричне зображення нижньої та верхньої ціни гри Джерело: [16; с. 435].
На цьому ж рисунку можна розглянути і геометричну інтерпретацію оптимальних стратегій противника В. Дійсно, частка З наведених міркувань легко зробити висновок, що гру 2´2 можна розв’язати елементарними прийомами. Аналогічно може бути розв’язана гра 2´ n, тобто коли гравець А має лише дві стратегії, а гравець В – n. У такому разі на рисунку слід зобразити перетин n прямих, що відповідатимуть n стратегіям гравця В. Мінімальні виграші гравця А являтимуть собою також ламану лінію, максимальне значення якої і визначатиме оптимальну стратегію для гравця А (рис. 1.5).
Рис. 1.5. Оптимальна стратегія для гравця А Джерело: [16; с. 436].
Можна також розв’язати і гру m ´2, з тією різницею, що необхідно визначати не нижню величину виграшу, а верхню і знаходити не максимальне з можливих значення, а мінімальне.
|
||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 153; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.222.47 (0.007 с.) |

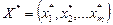 і
і  , що дають змогу отримати виграш:
, що дають змогу отримати виграш: .
.
 (1.4)
(1.4)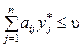
 (1.5)
(1.5) Вj
Ai
Вj
Ai
 . Необхідно знайти змішані стратегії та ціну гри. Позначимо шукані значення ймовірноcтей застосування «чистих» стратегій гравця А через
. Необхідно знайти змішані стратегії та ціну гри. Позначимо шукані значення ймовірноcтей застосування «чистих» стратегій гравця А через  , а для гравця В – через
, а для гравця В – через  [13; с. 42].
[13; с. 42].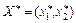 , то [16; с. 432]:
, то [16; с. 432]: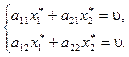 (1.6)
(1.6) , то
, то  . Підставивши цей вираз у систему рівнянь (1.6), отримаємо:
. Підставивши цей вираз у систему рівнянь (1.6), отримаємо: .
. , маємо:
, маємо: , (1.7)
, (1.7) =
=  . (1.8)
. (1.8)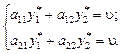 (1.9)
(1.9) , то
, то  .
. .
. , маємо:
, маємо: , (1.10)
, (1.10) . (1.11)
. (1.11) (або
(або  ) в будь-яке з рівнянь (1.6) або (1.9):
) в будь-яке з рівнянь (1.6) або (1.9): . (1.12)
. (1.12) Вj
Ai
Вj
Ai


 стратегії В1 в оптимальній змішаній стратегії
стратегії В1 в оптимальній змішаній стратегії 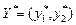 дорівнює відношенню довжини відрізка КВ2 до суми довжин відрізків КВ 2 та КВ 1 на осі І:
дорівнює відношенню довжини відрізка КВ2 до суми довжин відрізків КВ 2 та КВ 1 на осі І:  .
.