
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Неперервність елементарних функцій.
Розглянемо питання про неперервність елементарних функцій. Як ми знаємо, це функції, які утворено з основних елементарних функцій за допомогою скінченного числа арифметичних дій та операцій суперпозиції. Отже, якщо ми доведемо, що всі основні елементарні функції неперервні в своїй області визначення, то тим самим доведемо, що елементарні функції також неперервні в своїй області визначення. 1. Степенева функція з натуральним показником. Функція
Раціональна функція
2. Степенева функція з раціональним показником. Розглянемо функцію Функція Розглянемо тепер степеневу функцію з цілим від’ємним показником, тобто функцію Нехай тепер
Функція Враховуючи неперервність раціональних функцій в їх області визначення, тепер можна стверджувати, що ірраціональні функції також неперервні в їх області визначення. Отже алгебраїчні функції неперервні в їх області визначення. 3. Тригонометричні та обернені тригонометричні функції. Лема. Для
Доведення. Доведемо це співвідношення спочатку для
Рис. 48.
Побудуємо коло з центром у початку координат і радіусом 1. Проведемо радіус Через точку
Або:
Оскільки тут
Або:
Оскільки функції Лема.
Доведення. Якщо
Теорема. Функції Доведення. Нехай
Звідси і з нерівності (24.2) маємо:
Функція Теорему доведено. Наслідок 1. Функція Дійсно, функція Наслідок 2. Функція 4. Показникова та логарифмічна функції. Доведемо, що функція
Якщо ми доведемо, що Скористаємось рівністю (див. п.10, приклад 2):
Звідси випливає, що й
А тоді
Якщо тепер
або
Отже, внаслідок довільності Нехай тепер
Оскільки функція Функція Таким чином ми довели, що всі основні елементарні функції неперервні в їх області визначення. Звідси випливає твердження. Всі елементарні функції неперервні в їх області визначення.
|
||||||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 801; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.188.64 (0.038 с.) |
 неперервна на
неперервна на  , оскільки
, оскільки 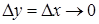 при
при 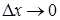 для будь якого
для будь якого  . Тому функція
. Тому функція 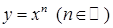 неперервна на
неперервна на 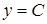 , де
, де 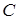 – стала, неперервна на
– стала, неперервна на 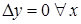 ), то функція
), то функція 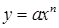 , де
, де 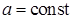 , також неперервна на
, також неперервна на 
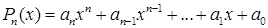 є неперервною на
є неперервною на 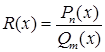 , де
, де 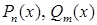 – многочлени степеня
– многочлени степеня  відповідно, неперервна як частка двох неперервних функцій в усіх точках множини
відповідно, неперервна як частка двох неперервних функцій в усіх точках множини 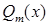 . Тобто в усіх точках, де функція
. Тобто в усіх точках, де функція 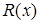 визначена.
визначена.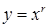 , де
, де 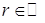 . Якщо
. Якщо 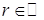 , і
, і  непарне, то функція
непарне, то функція 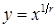 , яка також неперервна та зростаюча на
, яка також неперервна та зростаюча на 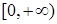 . Тоді така функція має обернену функцію
. Тоді така функція має обернену функцію 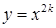 ,
, 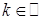 ,
, 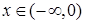 також має обернену – це функція
також має обернену – це функція 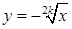 .
.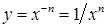 ,
,  . Вона визначена і неперервна на множині
. Вона визначена і неперервна на множині 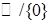 . При
. При 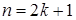 (
(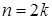 (
(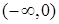 та
та 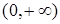 .
.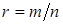 , де
, де 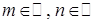 . За означенням:
. За означенням: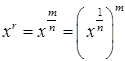 ,
, 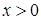 .
.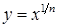 неперервна і зростаюча на
неперервна і зростаюча на 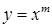 неперервна на
неперервна на 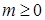 і спадна при
і спадна при 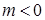 . Тому функція
. Тому функція 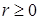 і спадна, якщо
і спадна, якщо 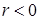 .
.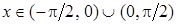 виконано:
виконано: . (24.1)
. (24.1)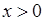 . Виконаємо наступну геометричну побудову (рис. 48).
. Виконаємо наступну геометричну побудову (рис. 48).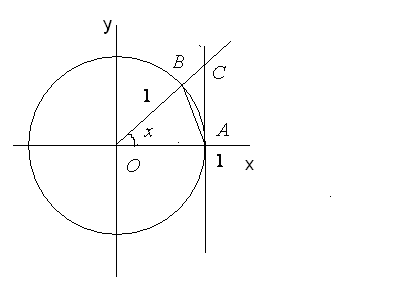
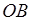 цього кола під кутом
цього кола під кутом  (в радіанах) до додатного напряму осі абсцис, причому продовжимо його за коло.
(в радіанах) до додатного напряму осі абсцис, причому продовжимо його за коло.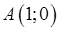 проведемо пряму, перпендикулярну осі абсцис (дотичну до кола). Точку перетину цієї прямої і продовження радіусу
проведемо пряму, перпендикулярну осі абсцис (дотичну до кола). Точку перетину цієї прямої і продовження радіусу  . Тоді площа трикутника
. Тоді площа трикутника  буде дорівнювати
буде дорівнювати 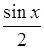 , площа сектора
, площа сектора 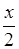 , а площа трикутника
, а площа трикутника 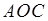 дорівнює
дорівнює 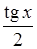 . Очевидна подвійна нерівність:
. Очевидна подвійна нерівність: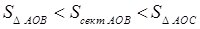 .
.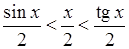 , тобто
, тобто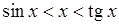 .
.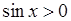 , то поділивши на
, то поділивши на 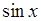 , матимемо:
, матимемо: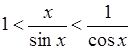 .
.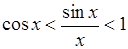 .
. та
та  парні, то співвідношення (24.1) виконано й для
парні, то співвідношення (24.1) виконано й для  .
.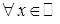 виконано:
виконано: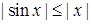 . (24.2)
. (24.2)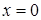 , то нерівність (24.2) виконано. Нехай
, то нерівність (24.2) виконано. Нехай 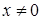 . Якщо
. Якщо 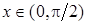 , то з (24.1) маємо:
, то з (24.1) маємо: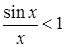 , з чого одразу випливає (24.2). Оскільки функція
, з чого одразу випливає (24.2). Оскільки функція 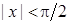 . А якщо
. А якщо 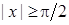 , то також виконується, оскільки
, то також виконується, оскільки 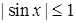 і
і 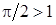 .
.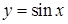 ,
, 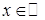 . Надамо значенню
. Надамо значенню 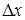 і розглянемо відповідний приріст функції
і розглянемо відповідний приріст функції 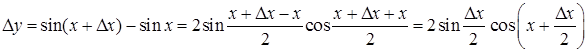 .
.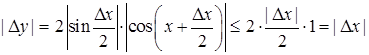 , отже
, отже 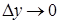 при
при 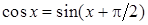 .
.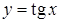 неперервна на множині
неперервна на множині 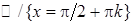 , а функція
, а функція 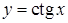 неперервна на множині
неперервна на множині 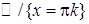 .
.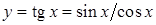 неперервна як частка двох неперервних функцій в усіх точках множини
неперервна як частка двох неперервних функцій в усіх точках множини 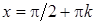 . Функція
. Функція 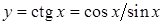 неперервна в усіх точках множини
неперервна в усіх точках множини  .
.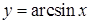 ,
, 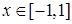 неперервна як обернена до функції
неперервна як обернена до функції 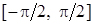 (див. п. 16). Функція
(див. п. 16). Функція 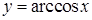 ,
, 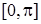 . Функція
. Функція 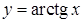 неперервна на
неперервна на 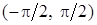 . Функція
. Функція 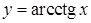 неперервна на
неперервна на 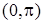 .
.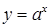
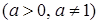 неперервна на
неперервна на 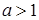 . Нехай
. Нехай 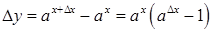 .
.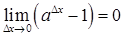 , то виконуватиметься
, то виконуватиметься 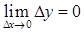 , тобто функція
, тобто функція 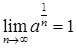
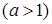 .
.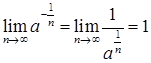 .
.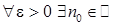 таке, що
таке, що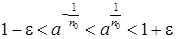 .
.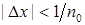 , тобто
, тобто 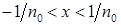 , то, оскільки при
, то, оскільки при 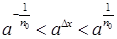 , звідки
, звідки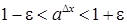 ,
,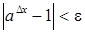 , звідки внаслідок довільності
, звідки внаслідок довільності  випливає, що
випливає, що 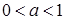 . Тоді
. Тоді 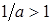 , і
, і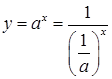 .
.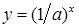 за доведеним вище неперервна, і
за доведеним вище неперервна, і 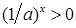
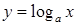
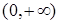 як обернена до неперервної та зростаючої функції
як обернена до неперервної та зростаючої функції 


